Технические науки / 4. Транспорт

Неженцев А.Б., Аветисян С.М., Косоногова Л.Г., Орлов С.А.

Восточноукраинский национальный университет им. В. Даля

Моделирование переходных процессов при
опускании грузов кранами мостового типа

Вследствие повышения интенсификации погрузочно-разгрузочных работ и рабочих скоростей крановых механизмов остро стоит проблема снижения динамических нагрузок в канатах и металлоконструкциях грузоподъемных кранов, а также плавной «посадки» грузов и их точного позиционирования. Поскольку одним из наиболее эффективных путей осуществления плавного и точного опускания груза является применение динамического торможения, то в панелях управления силовыми и магнитными контроллерами механизмов подъема устанавливают устройства, реализующие указанный вид торможения двигателем (например, контроллеры ККТ65А, ККТ69А, ТСД) [1].

Вместе с тем, не смотря на очевидные преимущества динамического торможения при опускании грузов и выпускаемые промышленностью панели управления, этот режим торможения используется редко. Одной из причин является необоснованный (иногда - неприемлемый) выбор механических характеристик в режиме динамического торможения, что может привести к значительному увеличению времени опускания груза, или не даст снизить динамические нагрузки. Отсутствие обоснованных рекомендаций не только существенно снижает эффект от применения динамического торможения, но и может дискредитировать прогрессивный вид торможения при неумелом использовании.

Поскольку публикаций, касающихся переходных процессов при опускании груза и в частности – в режиме динамического торможения практически нет, то в данной работе предлагается математическая модель и результаты исследований влияния различных факторов на динамические нагрузки при опускании груза мостовым краном в режиме динамического торможения.

Процесс опускания груза состоит из нескольких этапов, а переходные процессы при опускании груза краном мостового типа, представленного трехмассовой динамической моделью (см. рис. 1), описываются следующими системами дифференциальных уравнений:

- на первом этапе (опускание груза при работе двигателя в режиме силового спуска, рис. 1б), а также - на втором этапе (опускание груза при работе двигателя в генераторном режиме, рис. 1в)

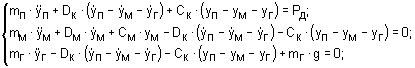(1)

- на третьем этапе (опускание груза при работе двигателя в режиме динамического торможения до момента касания грузом основания, рис. 1в)

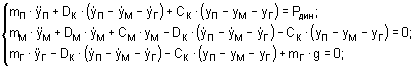(2)

- на четвертом этапе (после того как груз коснулся основания, происходит ослабление канатов, рис. 1г)

(3)

При этом начальные условия являются ненулевыми и определяются по следующим выражениям:

(4)

Приведенная к канатам сила привода Р_Д определяется по формулам:

- в двигательном и генераторном режимах при опускании груза

; (5)

- в режиме динамического торможения

, (6)

где m_П, m_М, m_Г – приведенные массы, соответственно, вращающихся частей привода подъема, средних частей моста и порожней тележки, груза; y_П, y_М, y_Г – пути, проходимые, соответствующими массами от начала координат; С_М и С_К – коэффициенты жесткости металлоконструкции крана и канатов; D_M и D_K – коэффициенты демпфирования колебаний металлоконструкции крана и канатов; P_Д – приведенная к канатам сила двигателя; ; - постоянные для j-ой искусственной характеристики двигателя; - критический момент двигателя; - критическое скольжение на j-ой механической характеристике; - скорости подъема груза, соответствующие синхронной и текущей частотам вращения ротора двигателя; - передаточное число привода; - радиус барабана; - КПД механизма подъема.

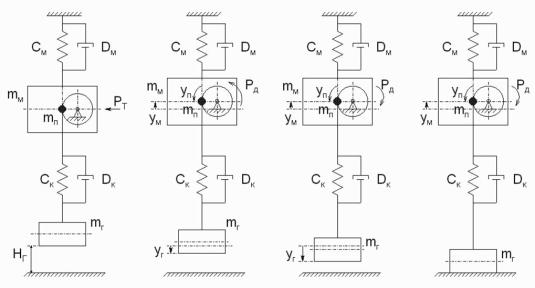
а) б) в) г)

Рис. 1. Трехмассовая модель мостового крана при опускании груза

Для интегрирования систем нелинейных дифференциальных уравнений (1, 2, 3) совместно с выражениями (4, 5, 6) численным методом разработана многофункциональная компьютерная программа [2], позволяющая с высокой точностью рассчитывать значения и строить графики изменения перемещений, скоростей и ускорений приведенных масс, нагрузок в металлоконструкции и канатах при опускании грузов в различных режимах.

На примере мостового крана грузоподъемностью 20/5т и пролетом 28,5м было исследовано множество переходных процессов при опускании грузов. В результате их обработки построены графики (см. рис. 2-4). На рис. 2 приведены графики зависимости времени опускания номинального груза от высоты и механических характеристик электропривода в режиме динамического торможения мостовым краном г/п 20/5т.

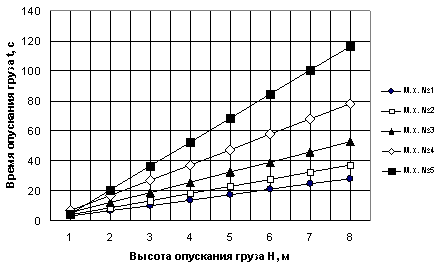
Рис. 2. Графики зависимости времени опускания номинального груза
от высоты и механических характеристик в режиме динамического
торможения мостовым краном г/п 20/5т

На рис. 3 приведены графики зависимости коэффициента динамичности металлоконструкции, а на рис. 4 - коэффициента динамичности в канатах мостового крана г/п 20/5т от высоты и механических характеристик электропривода при опускании номинального груза в режиме динамического торможения.

Анализ результатов исследований при опускании груза показал, что в отличие от подъема «с подхватом» коэффициенты динамичности нагрузок в канатах К_к и металлоконструкции крана К_м зависят от высоты опускания. Они уменьшаются до 9% при увеличении высоты опускания до 8м. Наименьшие коэффициенты динамичности К_к и К_м были получены при опускании по первой механической характеристике, наибольшие – по третьей. Отметим, что самым быстрым спуск груза был на первой механической характеристике, а наиболее медленным – на пятой.

Таким образом, разработанные математическая модель мостового крана и программное обеспечение позволяют с высокой точностью рассчитывать нагрузки в металлоконструкции и канатах, перемещения, скорости и ускорения элементов крана и груза при его опускании в различных режимах.

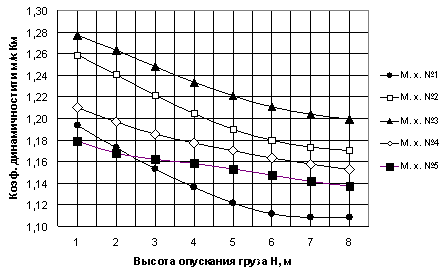
Рис. 3. Графики зависимости К_м от высоты и механических характеристик
при опускании номинального груза в режиме динамического торможения

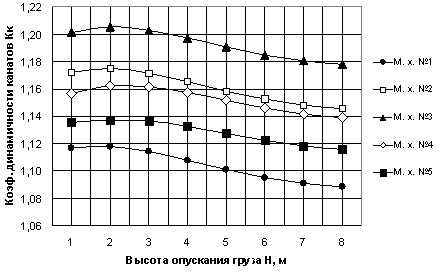
Рис. 4. Графики зависимости К_к от высоты и механических характеристик
при опускании номинального груза в режиме динамического торможения

Литература

1. Яуре А.Г., Певзнер Е.М. Крановый электропривод: Справочник.- М.: Энергоатомиздат,1988.- 344 с.

2. Аветисян С.М., Неженцев А.Б. Программное обеспечение для исследования переходных процессов грузоподъемных кранов (часть 2: при работе механизмов подъема грузов // Підйомно-транспортна техніка, № 1(9). - Дніпропетровськ, 2004. – с. 83-95.