Карачун В.В., Мельник В.М., Савченко О.В.,

Чередниченко Д.А., Пригорницька К.І.

Національний технічний університет України «КПІ»

ОСНОВНІ КІНЕМАТИЧНІ ХАРАКТЕРИСТИКИ РУХОМИХ ОБ’ЄКТІВ

Всім точкам рухомого об’єкту в загальному випадку притаманні різні за структурою переміщення. Тому, аналізуючи кінематику апаратів, природно починати з виявлення особливостей руху окремих його точок. Окрім того, деякі практичні задачі переміщення матеріальних тіл можуть бути вирішені безпосередньо на фундаменті результатів аналізу руху окремої точки.

Неперервну криву, за якою рухається точка, іменують траєкторією (годограф радіус-вектора, від грецьк. hodós – шлях, рух та ... граф). Траєкторія слугує геометричним місцем кінців радіус-вектора і має тенденцію змінюватися у часі. В задачах небесної механіки траєкторію іменують орбітою. Якщо траєкторія являється прямою лінією, то рух точки називають прямолінійним. В інших випадках – криволінійним. Перший, як видно, постає частковим від другого.

Основними просторово-часовими (кінематичними, від грецьк. kinematos – рух) характеристиками руху точки постають її положення, швидкість та прискорення.

Розподіл швидкостей в апараті. Для обчислення швидкості довільної точки рухомого об’єкту, як відомо, слід здиференціювати у часі геометричне рівняння

.

При виконанні операції диференціювання слід пам’ятати, що величини , , – сталі, а , , , – змінні у часі. Отже, швидкість точки тіла дорівнює:

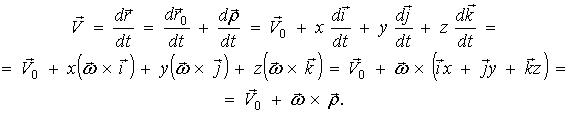(1)

В скалярній формі виразу (1) відповідні три співвідношення:

(2)

З формули (1) походить, що лінійна швидкість довільної точки фюзеляжу дорівнює геометричній сумі двох складових – вектора швидкості полюса (однакової для всіх точок апарата) та вектора , який залежить від положення точки.

Вектор являє собою швидкість, яку мала б матеріальна точка за умови поступального руху апарату з цією швидкістю.

Вектор окреслює швидкість, яку мала б ця точка за умови тільки обертального руху корпуса апарату навколо полюса (центра мас, чи центра величини об’єкта). Тому вектор іменується миттєвим.

Таким чином, лінійна швидкість довільної точки фюзеляжу є рівнодіюча швидкості поступального руху точки разом із полюсом та швидкості обертального навколо полюса руху відносно миттєвої осі, що проходить через полюс.

Формули (1), (2) мають фундаментальне значення для аналізу кінематики корпуса рухомого об’єкту. Відносно обраної непорушної координатної системи рух апарату буде цілком визначений, якщо обрана довільна точка – полюс та задані як функції часу два вектори і . Проекції цих векторів на рухому, зв’язану, систему координат будемо іменувати характеристиками руху корпуса апарату.

Лінійна швидкість полюса. В загальному випадку, вектор лінійної швидкості полюса може мати довільний напрямок як відносно опорної, так і відносно зв’язаної системи координат. І тому, його можна завжди охарактеризувати за допомогою власної величини та двох кутів між ним та осями обраної системи.

Якщо йдеться про рух апарату в середовищі, що чинить в’язкий опір – повітря, вода тощо, – тоді обидва зазначені кути вимірюються між вектором швидкості руху та осями, жорстко зв’язаними з корпусом. Причина такого вибору криється в тому, що головний вектор і головний момент сил опору середовища залежать, в основному, від величини швидкості та орієнтації вектора відносно фюзеляжу.

З оглядом на це, з полюсом поєднують ще одну систему координат – . Взаємне розташування швидкісної та зв’язаної системи наведене на рис. 1. За поздовжню площину об’єкта прийнята , вісь – напрямлена на правий борт.

Система координатних осей зв’язана тільки з вектором швидкості полюса. Відносно фюзеляжу вона може бути повернута, бо кути атаки і ковзання являються функціями часу, тобто ; .

Відповідно до рис. 1, складові швидкості полюса на осі зв’язаної системи дорівнюють:

; ; . (3)

Слід мати на увазі, що проекції , , самі по собі не в змозі повністю охарактеризувати поступальне переміщення полюса. Воно може бути визначене за допомогою співвідношень (3) та напрямних косинусів між зв’язаною і нерухомою системами відліку.

Миттєва кутова швидкість. Для обчислення миттєвої кутової швидкості об’єкту можна скористатися виразом (1)

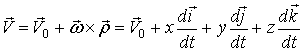. (4)

Помножимо обидві частини цього виразу на орти , , :

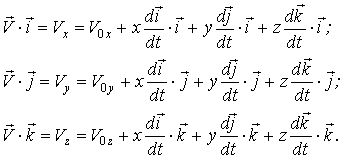(5)

Спростимо формули. Вектори , , зв’язані між собою очевидними співвідношеннями –

; ; ; ; ; .

Отже,

; ;

; ; (6)

; .

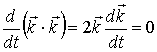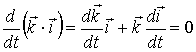Таким чином, співвідношення набувають вигляду:

(7)

Позначимо:

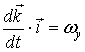; ; . (8)

Тоді проекції лінійної швидкості довільної точки корпуса об’єкта на осі , , можна навести наступним чином:

(9)

що у векторній формі відповідає виразу (1):

Зазначене дозволяє стверджувати, що лінійна швидкість будь-якої точки корпуса рухомого апарату обчислюється геометричною сумою двох складових – вектора , однакового для всіх точок фюзеляжа, та вектора , що залежить від місцезнаходження обраної точки, а на осі, жорстко пов’язані з об’єктом, має, відповідно, наступні складові: , та .

Для знаходження миттєвої кутової швидкості корпусу об’єкта слушно скористатися виразами (8):

(10)

Оскільки напрямні косинуси завжди можна навести за допомогою кутів Ейлера, тому і проекції миттєвої швидкості , згідно (10), також можна обчислити за допомогою цих кутів та їх перших похідних у часі.

Разом з тим, використання наведеного виразу (10) недоцільне внаслідок його громіздкості. Скоріше приводить до мети інший шлях. Констатуємо головне.

Відповідно структури сферичного руху апарату навколо полюса т. О, він здійснює три обертальні рухи з кутовими швидкостями , , , вектори яких виходять з точки О і напрямлені вздовж відповідної осі повороту, тобто ці три вектори перетинаються в одній точці, в полюсі. Тому

. (11)

Проектування на осі рухомої системи координат дає:

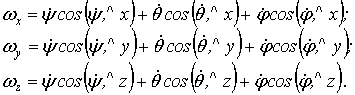(12)

Аналогічно в проекціях на опорну систему координат :

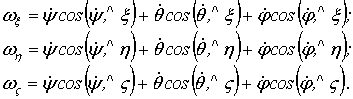(13)

Наприклад, для варіанту послідовності кутів Ейлера , , , проекції миттєвої кутової швидкості апарату на осі рухомої системи координат та нерухомої становлять:

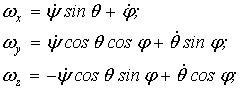(14)

(15)

Розподіл прискорень. За векторного задання руху об’єкта, розподіл прискорень, як відомо, визначається дворазовим диференціюванням у часі радіус-вектора довільної точки корпуса, або одноразовим диференціюванням у часі вектора швидкості цієї точки, тобто, згідно формули (1), маємо:

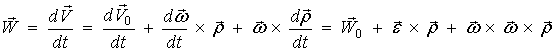. (16)

Перший доданок в правій частині цього виразу є прискорення полюса, другий і третій – відповідно, обертальне та доосьове прискорення. Вектори та величини цих складових обчислюються за відомими формулами.