К.т.н. Койбагаров С.Х.

Семипалатинский государственный университет имени Шакарима

ИССЛЕДОВАНИЕ ПРОЦЕССА ТЕРМООБРАБОТКИ В КАПИЛЛЯРНО-ПОРИСТЫХ ТЕЛАХ ПРИ НАГРЕВЕ

Нагрев различных капиллярно-пористых тел с целью их термообработки мощными импульсами микро- и миллисекундной длительности находит в последнее время все большее применение в промышленности в процессе работы термомасообменных аппаратах [1,2]. Для отработки режимов нагрева рассматриваемых тел, позволяющих свести к минимуму действия деформационных явлений, сопровождающих данный процесс, необходимо с достаточной степенью точности знать не только температуру на облучаемой поверхности, но и профиль распределения температуры по толщине тел. Получить такую информацию экспериментальным путем не представляется возможным из-за отсутствия приборов, позволяющих измерять температуру объектов за время действия импульса. В этом случае разработка математической модели процесса и проведение на ее основе численных экспериментов для широкого набора характеристик нагрева имеет большое практическое значение.

Применительно к процессу термообработки различных коллоидно-капиллярных материалов задача об импульсном нагреве может быть описана следующей системой дифференциальных уравнений:

, (1)

, (2)

, (3)

, (4)

где 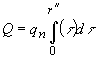- заданная плотность энергии импульса.

Задача (1) -(4) рассматривается в областях W=(0<х<d, 0<t<t^m).

Решение задачи находилось с помощью метода конечных разностей. Были проведены расчеты температурных: профилей по толщине, при облучении ее импульсами различной временной формы и плотностью энергии в импульсе, меняющейся в пределах 60-120 Дж/см. В наиболее общем случае форма импульса аппроксимировалась трапециевидной функцией f(l), удовлетворяющей условиям:

f(0)=A=const, f(t₁£t£t₂)=1,

f(t₃)=B=const, f(t^¢¢¢)=0.

Зависимость теплофизических свойств rС(Т) и l(Т) принималась в соответствии с данными (2) и аппроксимировалась степенными функциями Т для различных температурных интервалов: 293-1100 К: 1230-1230; 1230-1409 и при Т > 1400 К. Для сравнения были проведены также соответствующие расчеты при постоянных значениях l и rС.

Форма распространение тепла при прочих равных условиях определяет

предельную температуру нагрева Т_m и временной профиль температурного перепада по толщине пластины DТ(t). Максимальная температура нагрева Т_m определяется длительностью промежутка Dt=t₂-t_1. С уменьшением величины D при одинаковом значении Q уменьшается Т_m и увеличивается DТ. К концу процесса температура по толщине материала выравнивается. В то же время при задании потока теплоты нагрев происходит, за исключением начального периода, при постоянном перепаде DТ. Представление временной зависимости энергии при нагреве в виде прямоугольной функции является первым приближением к реальному ее распределению. Поэтому рассмотрение такой модели процесса может привести к ошибочным выводам при оценке физических процессов (например, диффузии примесей) процессе нагреве.

Учет температурой зависимости теплофизических характеристик приводит к изменению профиля температурного поля, но оказывает незначительное влияние на кинетическую кривую нагрева облучаемой поверхности. При этом существенно меняется не только максимальная величина температурного перепада по толщине пластины, но и сам характер зависимости. Нагрев идет с нарастающим Т. Максимальный перепад Т наблюдается с некоторым запаздыванием после перехода на нисходящую ветвь. Концу импульса температура по толщине пластины выравнивается.

Выявлена существенная зависимость Т и DТ от толщины пластины. Так, например, при уменьшении толщины тела в 2,5 раза пропорционально увеличивается максимальная температура нагрева Т_m в импульсе, а максимальный температурный перепад по толщине возрастает примерно в 1,25 раза. Иначе говоря, в условиях существенно нестационарного импульсного нагрева капиллярно-пористых тел имеет место возрастание вклада в Т_m поверхностного нагрева тел при уменьшении их толщины.

Проведенная оценка влияния теплообмена с окружающей средой показала, что при продолжительностях импульсах c конвективным теплообменом, а также собственным излучением тел в исследованных пределах изменения Q = 60-120 Дж/см можно пренебречь с точностью до 1% и рассматривать процесс как адиабатический нагрев.

Была рассмотрена модель процесса, когда весь тепловой поток поглощается поверхностью тела. В этом случае при переходе от источника тепла к тепловому потоку на внешней границе и прочих равных условиях увеличивается температура поверхности в течение всего времени действия распространение тепла, возрастает максимальный перепад по толщине материала.

Таким образом, на основании разработанных моделей процесса нагрева произведена оценка влияния различных характеристик внутреннего (l,c,r,d) внешнего (Q,a,f(t),e} теплопереноса на развитие температурных полей в обрабатываемых: телах, что в свою очередь позволяет производить выбор оптимальных параметров (энергетических к временные) импульсного энергоподвода обеспечивающих протекание процессов термообработки при наименьших перепадах температуры, а следовательно, и с минимальными напряженными состояниями.

Условные обозначения

с - теплоемкость, k - коэффициент поглощения, R - отражательная способность, Т₀ - начальная температура тела, Т_ср - температура среды, l - коэффициент теплопроводности, р - плотность, d- толщина, e - степень черноты, s -постоянная Стефана-Больцмана, q_n - плотность теплового потока.

Литература

1 Двуреченский А.В., Качурин Г.А., Нидаев Е.В., Смирнов Л.С. Импульсный отжиг полупроводниковых материалов - М.: Наука, 1962.

2 Охотин А.С, Пушкарский А.С., Горбачев В.В. Теплофиэические свойства полупроводников. - М: Атомиздат, 1972.