Технические науки/2. Механика

 

К.т.н. Касымханов С. Ж., д.т.н. Бакиров Ж. Б.

 

Восточно-Казахстанский государственный технический университет,

Карагандинский государственный технический университет,

Республика Казахстан

 

Математическая модель и методика расчета уплотнения  формовочной смеси

 

В настоящее время большую часть отливок получают в разовых песчаных формах. От качества формы зависит точность и состояние поверхности отливки. Качество формы зависит от состава смеси, ее плотности и распределения плотности по высоте опоки. С увеличением плотности возрастают прочность и чистота поверхности отливки, уменьшается газопроницаемость и склонность формы к размыву. Анализ процесса уплотнения формовочной смеси необходимо не только для управления качеством отливок, но и для создания высокопроизводительного и надежного оборудования путем управления количеством, продолжительностью и мощностью импульсов.

Особенностью динамического нагружения является то, что сжимающие напряжения достигают значительной величины, но действуют кратковременно. При этом смесь не успевает уплотниться, и нужны повторные нагружения, следовательно, плотность смеси зависит не только он величины напряжений, но и от времени их действия. Это говорит о том, что для анализа процесса уплотнения при динамических нагрузках необходимо учитывать вязкость среды.

В настоящее время получен ряд экспериментальных зависимостей для расчета плотности при различных видах динамического нагружения: ударное, прессово-ударное, встряхивание, импульсное, гравитационное и т.д. Однако они применимы только для специфических условий нагружения и для отдельных грунтов и ПГС. Для получения аналитических зависимостей необходимо исследовать процесс уплотнения на основе реологической модели, наиболее адекватно описывающей основные свойства среды: упругость, вязкость и пластичность. Наиболее распространенной в этом плане является полуэмпирическая формула, полученная Г.М.Орловым на основе трехэлементной модели путем игнорирования упругих деформаций [1].

На основе анализа многочисленных экспериментов в данной работе в основу расчета плотности формовочной смеси при динамическом нагружении принята пятиэлементная реологическая модель, показанная на рисунке 1.

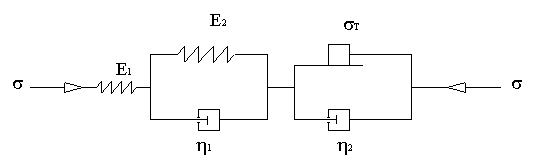
Рисунок 1. Реологическая модель среды

Первый элемент модели (пружина 1 с модулем упругости Е1) учитывает способность среды мгновенно получать упругие деформации. Параллельно соединенные пружина 2 и демпфер 1 с коэффициентом вязкости  отражают упруговязкие свойства среды, приводящие к упругому последействию. Последняя часть модели, состоящая из демпфера 2 и пластического тела Сен-Венана, отображает вязкопластические свойства среды и включается в работу только при напряжении, превосходящем предел текучести материала . Чтобы учесть тот непреложный факт, что среда может уплотняться только при возрастании напряжения, мы должны считать предел прочности зависящим от текущей плотности среды, что ранее обнаружено в ходе экспериментов и описано эмпирическими зависимостями.

Запишем уравнения состояния среды согласно представленной модели:

;                         (1)

.                                       (2)

где  – деформации пружин;  – суммарные напряжения и деформации.

Определим связь между напряжением и деформацией для первой части модели, состоящей из двух пружин и демпфера 1. Из второго соотношения уравнений (1) при граничных условиях , получаем

Учитывая, что   из первого соотношения получаем

    ,                               (3)

где  , а  Ес  статический модуль упругости.

Определим связь между деформацией и плотностью смеси. Пусть при приложении нагрузки образец, имеющий начальную длину l0 сжался, и его длина стала l . Относительное сжатие части образца длиной х будет равно dx/x, где dx  – абсолютное сжатие рассматриваемой части. Тогда полная относительная деформация равна сумме относительных сжатий отдельных участков:

.

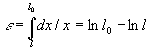Отсюда следует dε = – dl/l. Далее учтем, что , где  – масса, плотность и площадь сечения образца. Подставив l и dl в предыдущее соотношение, получим:  

.                                                 (4)

Решая это уравнение, находим , где – начальная плотность среды (при ). Теперь с учетом выражения (3) имеем:

                                       (5)

При напряжениях превышающих предел текучести из уравнения (2) следует:

,                                               (6)

где  – деформация соответствующая пределу текучести и определяемая по формуле (3);  пластическая деформация;  – разность между текущим моментов и началом пластического течения.

Далее из уравнения (2) с учетом (4) можно записать:   .

Решая этой уравнение, получим:

                                           (7)

где  – плотность при напряжении    и определяемая по формуле (5).

Так как предел текучести зависит от плотности, которая в свою очередь зависит от текущего значения напряжения, то расчет изменения плотности во времени приходится вести шаговым методом. Тогда в формуле (7)  ,  можно заменить на напряжение и плотность в предыдущий момент времени, а за   принять шаг по времени.

Рассматриваемый этап вязкопластического уплотнения продолжается до тех пор, пока растет пластическая деформация; далее начинается процесс разгрузки. Поэтому при расчете плотности необходимо зафиксировать напряжение и максимальные значения плотности и деформации перед разгрузкой:

Процесс разгрузки происходит по закону Гука:

С учетом условия  при  и выражений (4) и (8), находим:

                              (8)

Этот процесс продолжается до тех пор пока напряжение не станет равным нулю.

Многочисленные эксперименты разных авторов показывали, что физико-механические свойства смеси зависят не только от состава и влажности, но и от её плотности. Обработка экспериментальных данных позволяет получить зависимость реологических параметров от плотности. Так как при встряхивании напряжение и плотность смеси меняется по высоте опоки, то для расчета плотности необходима дискредитация не только по времени, но и по высоте слоя.

Изложим теперь методику послойного расчета плотности формовочной смеси при встряхивании. При ударе стола о станину с некоторой начальной скоростью   стол и опока со смесью резко тормозятся и во всех слоях смеси возникают инерционные силы, вызывающие сжимающие напряжения. Если пользоваться контактно-классической теорией удара, то скорость стола можно определить по формуле:

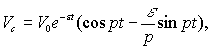                                        (9)

где   – коэффициент затухания колебаний;    – частота колебаний;

При этом продолжительность удара определяется по формуле:

Под действием сжимающих напряжений происходит уплотнение смеси по всей высоте опоки до максимального значения . При этом толщины всех слоёв уменьшаются и каждое сечение движется в низ с определёнными скоростями и ускорениями. Разобьём высоту опоки  Н  на k – 1 слоев.

Масса любого слоя при уплотнении не изменяется, поэтому толщину j- го слоя в  i - ый момент времени можно определить по формуле:

                                          (10)

Расстояние от верхней границы  j - го слоя до начала координат равно:

                                              (11)

Абсолютные значения скорости и ускорения верхней границы слоя равны:

                                        (12)

где   – шаг по времени.

При расчёте сверху вниз надо задаться скоростью верхнего слоя, например,

Правильность выбора скорости контролируется по нижней грани условием:

                                            (13)

где  – допустимая погрешность по скорости.

При этом координата верхней грани определяется так:

                                    (14)

Скорость изменения напряжений в сечениях определяется выражением [1]

                          (15)

где Р,  А – периметр и площадь опоки;

ξ – коэффициент бокового давления;

f – коэффициент трения смеси о стенку опоки.

Тогда напряжения в слоях будут равны:

                                    (16)

Приведём последовательность (блок-схему) послойного расчета уплотнения формовочной смеси с использованием персональных компьютеров.

1.Задание и распечатка исходных данных:

2.Задание начальных условий:

 где – пластические деформации в сечениях.

3. Организация цикла по времени:

4. Вычисление скорости стола по формуле

5. Задание условий на поверхности смеси:

6. Вычисление координаты верхней грани по (14)

7. Организация цикла по слоям: .

8. Вычисление параметров реологической модели в слоях по эмпирическим формулам в зависимости от плотности слоя  

9. Вычисление плотности смеси в сечениях   – формулы (5,7,8).

10. Вычисление толщин слоев, координат, скоростей и ускорений сечений по формулам (1012):

11. Вычисление напряжений в сечениях по формулам (15) и (16) –

12. Конец цикла по слоям:

13. Проверка условия (13). Если оно выполнено, то продолжить расчеты, если нет, то  изменить скорость  и повторить послойный расчет с пункта 6.

14. Конец цикла по времени:

15. Распечатка расчетных параметров:  и т.д.

По приведенной блок-схеме составлена программа расчетов на языке Паскаль и проведен расчет плотности песчано-глинистой смеси влажности 3,2 % и сырой прочности 0,07 МПа с начальной плотностью  = 1000 кг/м при  = 1 м/с и размерах опоки 400×300×200 мм. Характеристики механической системы соответствуют встряхивающей машине модели 271:

 Смесь разбивалась на 10 слоев. Результаты расчетов для первого удара приведены на рисунке 2. Кривая 1 соответствует нижнему сечению, а кривая 2 – седьмому сечению. Чем ниже расположено сечение, тем выше интенсивность роста плотности. Интенсивность роста плотности сильно зависит от первоначальной плотности. Так при  = 1500 кг/м она на ладе составляет всего 1 % в отличие от 8,5 % на графике.   

 

 

 

 

 

 

 

 

 

 

 

 

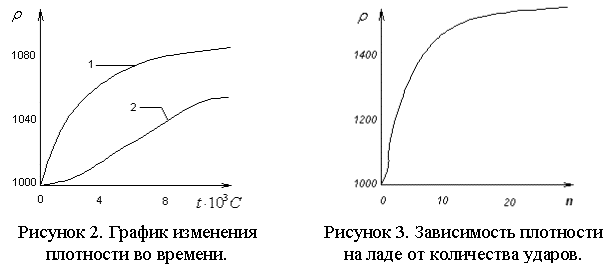
При увеличении числа ударов плотность сначала быстро возрастает, затем рост замедляется, а после определенного числа ударов вовсе прекращается. График изменения плотности на ладе (в нижнем сечении) от количества ударов показан на рисунке 3.

 

Литература:

1. Орлов Г.М. Автоматизация и механизация процесса изготовления литейных форм. – М.: Машиностроение, 1988. – 264 с.