Педагогические науки/5. Современные методы преподавания

К.ф.-м. н. Аксенова Е.Н.

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Национальный Исследовательский Ядерный Университет «МИФИ», Россия

К.ф.-м. н. Аксенова Н. П.

Физико-технологический институт Российской академии наук, Россия

Три составляющие успеха образовательного процесса

На современном этапе развития образовательного процесса значение умелой популяризации науки и знаний не уменьшилось, а возросло. Это обусловлено целым рядом причин.

Огромные, подчас отупляющие, потоки информации, широкая доступность информации, не относящейся к возрастной зоне актуального развития ребенка, и ее агрессивная направленность в части рекламы – все это порождает у детей потерю интереса к процессу познания. Другой опасной чертой современности является формализация мышления детей взамен развития у них творческого подхода в совокупности с интеллектуальным потенциалом. Эта тенденция связана с ранним приобщением детей к схематичным компьютерным играм. Указанные особенности являются объективными чертами современности, затрудняющими организацию полноценного образовательного процесса. Эти факторы усугубляются негативными моментами в организации самого учебного процесса. К ним следует отнести чрезмерную информационную нагрузку учащихся, связанную с наличием 7-8 информационно значимых уроков в день у старшеклассников и 6 уроков у средних и даже младших школьников, как следствия пятидневной школьной недели. Введение элементов алгебры в классах начальной школы и замена арифметических методов решения задач алгебраическими мешает формированию логических навыков ребенка. Исключение из процесса изучения гуманитарных предметов пересказов приводит не только к недостаточному развитию речи учащихся, но также их умения выделять главное в материале любого предмета с последующим анализом. Снижает значение творческой составляющей учеников и введение тестовой системы проверки знаний.

Существует немало других обстоятельств, мешающих организации успешного образовательного процесса, но и перечисленных достаточно, чтобы понять, почему так важна сегодня популяризация знаний, призванная сохранить в ребенке врожденную пытливость ума и стремление познавать.

Противостоять негативным особенностям нашего времени и снизить их влияние на образовательный процесс можно, используя следующие методические принципы:

1. Баланс сложности. Материал должен методически последовательно отрабатываться и усложняться, неся в себе обучающую составляющую. При этом обязательным условием является соблюдение баланса сложности поставленной задачи.

2. Интерес учащихся. Изучаемый материал должен соответствовать зоне актуального развития учащегося, иными словами учащийся должен быть готов к заинтересованному восприятию материала.

3. Обратная связь. Процесс обучения должен быть построен так, чтобы дети, получая новые знания, имели желание и возможность проявить себя (иметь возможность самовыражения).

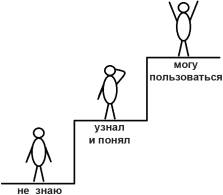Поговорим о балансе сложности. Любой процесс получения знаний можно рассматривать как интеллектуальную лестницу. Подъем по этой лестнице соответствует не просто получению новых знаний, но и введению их в личностный актив учащегося, развитию его личного интеллектуального потенциала. При макроскопическом рассмотрении изучение любой отдельной темы по любому предмету условно можно представить в виде двух ступенек.

Рассмотрим эти ступеньки детально. Подъем на первую ступеньку предполагает наличие необходимой концентрации внимания учащегося. А это возможно только при его заинтересованном восприятии материала, которое, в свою очередь, может быть обеспечено при условии соответствия материала зоне актуального развития учащегося.

Но еще более серьезная проблема состоит в преодолении второй ступени, восхождение на которую предполагает наработку учащимся навыков в результате самостоятельного выполнения заданий. Эту ступень можно представить состоящей из маленьких ступенек. Каждая из них - это освоение учащимся нового навыка или знания.

Необходимым условием успешного процесса обучения является последовательное усложнение задач и накопление освоенного материала. При этом высота каждой ступеньки, соответствующая сложности отдельной задачи, не должна превышать потенциала интеллектуального скачка учащегося U. Очевидно, что наилучший результат может быть достигнут в группе с единым или близким уровнем стартовых знаний. В этом отношении гораздо проще выстроить методику преподавания начал любого предмета, чем продолжения курса, т.к. в этом случае приходится начинать с пропедевтики пройденных ранее основ для подтягивания учащихся на единый начальный уровень знаний.

Потенциал интеллектуального скачка является индивидуальным параметром. Выбирая сложность задач для самостоятельной отработки материала учащимися, т.е. высоту мелких ступенек, приходится ориентироваться на средний потенциал скачка < U> . При этом для учащегося, имеющего заниженный потенциал U относительно среднего < U>, следует разбить слишком высокие для него ступеньки на несколько меньших по высоте, заменив сложное задание серией простых последовательно усложняющихся. Строго говоря, повышение U каждого учащегося является основной целью любого обучения, поэтому необходимо создать условия мотивации этого процесса посредством интереса учащихся и предоставления им возможности самовыражения.

Практика преподавания убеждает в том, что все выше сказанное справедливо для всех без исключения уровней обучения – от дошкольного до университетского. При этом наиболее веская мотивация учебного процесса должна присутствовать в начальной и средней школе. В этой ситуации популяризация знаний призвана не дать угаснуть врожденной пытливости ума и врожденному стремлению познавать, т.к. хорошо известно, что огонь легче поддерживать, чем разжигать.

Если материал сам по себе сух и, с точки зрения учащегося, не несет в себе явной мотивации к изучению, она должна быть организована методически за счет дополнительного носителя. В частности это относится к изучению математики.

Именно с этой целью разработан и успешно преподается курс занимательной математики и логики для начинающих. Курс представляет собой единый методический цикл «Сказка, рассказанная математиком» [1, 2, 3, 4, 5, 6]. Цель этого цикла – с помощью увлекательной сказочной формы ввести ребенка в мир математики, развивая его абстрактное, образное и логическое мышление, а также без изнурительного заучивания привить вычислительные навыки. Сказочная основа выбрана не случайно. Именно сказки лежат в зоне актуального развития детей, а современная популярность жанра фэнтези убеждает в том, что сказочные мотивы интересны и близки не только младшим школьникам. Увлеченные сказочным сюжетом, учащиеся сопереживают главным героям, решая задачи на фоне игровой мотивации. В текст авторских сказок, написанных с использованием бродячих сюжетов, вставлены задачи. Включившись в сказочные приключения, дети стремятся решать возникшие перед героями проблемы и не заметно для себя приобретают знания и нарабатывают математические навыки.

Продемонстрируем обозначенные методические принципы в действии на примере одной [4] из сказок цикла. Эта книга написана специально для развития у детей 6-8-летнего возраста абстрактного мышления, умения выделять главное в повествовании, а также для закрепления навыков сложения и вычитания в пределах 100. Сказка делится на 25 эпизодов, каждый из которых содержит вычислительными математическими заданиями и короткими сказками. Каждый сказочный эпизод, требует от ребенка вместе с главным героем оказать помощь каким-нибудь попавшим в беду зверькам или птенцам, произведя необходимые вычисления. Таким образом, у ребенка возникает нравственно положительная мотивация наработки вычислительных навыков. В результате учащийся с удовольствием решает не менее 30 примеров в каждом фрагменте и для визуального обозначения полученных арифметических ответов раскрашивает их соответствующим цветом, помогая тем самым потерявшимся зверькам найти свой дом или родителей. После этого, благодарные звери рассказывают свою звериную сказку.

Как показывает практика, одной из проблем, возникающих при обучении детей математике в начальной школе, является недостаточный уровень развития их абстрактного мышления. Это влечет за собой трудности ребенка при осмыслении условий задач, умения выделить главное в условии, обобщить условие конкретной задачи и выбрать метод ее решения. Для развития абстрактного мышления в процессе чтения ребенку предлагается зарисовывать каждый эпизод короткой сказки, заменяя ее действующие лица простейшими геометрическими фигурами. Затем по своим несложным картинкам дети легко пересказывают сказку.

В процессе развития сказочного сюжета методически усложняются задания:

а) количество и сложность примеров последовательно повышается, начиная от состава чисел первого десятка, затем вычисления десятками, счета во втором, третьем, четвертом десятках и в заключение наработки навыков сложения и вычитания с переходом через десяток;

б) удлиняются звериные сказки и усложняются их сюжеты.

В результате работы по этой книге дети не только нарабатывают вычислительные навыки, но и овладевают очень полезным методом пересказа, повышая свой интеллектуальный потенциал.

Другие сказки цикла знакомят учащихся с началами дискретной математики и различными системами счисления, методически развивая навыки решения логических задач и прививая любовь к математике.

Серия книг «Сказка, рассказанная математиком» может быть полезна для организации интересной работы на уроках, как в начальной, так и в средней школе, а также для самостоятельной работы родителей со своими детьми. Кроме того есть положительный опыт использования этого курса логики на вводных занятиях по программированию в старших классах. Ученики старших классов с удовольствием включались в сказочную математическую игру, а через несколько уроков с удивлением узнавали, что познакомились с началами дискретной математики. В настоящее время этот курс успешно используется в сфере дополнительного образования.

Литература:

1. Е.Н.Аксенова Сказка, рассказанная математиком. Иван-царевич и Анастасья

Прекрасная, М., Ступени знаний , 2002.

2. Е.Н.Аксенова Сказка, рассказанная математиком. Огонь в сердце, а разум в

голове, М., Ступени знаний 2003.

3. Е.Н.Аксенова Развитие логического мышления школьников, М., ВЛАДОС,

2006.

4. Е.Н.Аксенова, Н.П.Аксенова Сказка, рассказанная математиком. Колпак –

чуткие уши, М., Ступени знаний, 2009.

5. Е.Н.Аксенова, Н.П.Аксенова Сказка, рассказанная математиком. Путешествие в Арфиц, М., Ступени знаний, 2010.

6. Е.Н.Аксенова, Н.П.Аксенова Сказка, рассказанная математиком. К истокам математики, М., Ступени знаний, 2011.