Т.К.Оспанов, кандидат педагогических наук, профессор Национального педагогического университета имени

Абая. Республика Казахстан.

Технология обучения решению задач в начальных классах школ Республики Казахстан

Процесс обучения математике младших школьников в Республике Казахстан осуществляется технологией, которая ориентирована на формиро- вание предметной компетенций - знаний, умений, навыков и интеллектуаль- ное развитие личности. Она позволяет проектировать и реализовать модель взаимосвязей и взаимодействия деятельности обучающего и обучающихся адекватно цели и содержанию обучения математике в начальных классах школы.

Реализуемой в настоящее время на практике локальной технологии обучения решению задач в начальных классах школы присущи особенности, целевые ориентации, концептуальные положения, содержание образования, процессуальная характеристика.

Параметры целевой ориентации технологии обучения решению задач в начальных классах представлены в таблице и обусловлены необходимостью обучать всех в соответствии с требованиями государственного стандарта начального математического образования к обязательному уровню подго -товки учащихся.

Кл.-ы	Требования к обязательному уровню подготовки учащихся
1 кл.	-понимают смысл понятия задача; –знают особенности и существенные признаки задачи в одно действие; -решают простые задачи на сложение и вычитание
2 кл.	–знают особенности и существенные признаки задачи; в два действия; -решают задачи в одно и два действия на сложение и вычитание
3 кл.	-решают простые задачи на умножение и деление; -решают составные задачи (2-3 действия) на все арифметические действия, которые представляют собой различные комбинации простых задач
4 кл.	-знают особенности и существенные признаки задачи как особого вида математических упражнений; -знают составляющие компоненты задачи и этапы процесса ее решения; -решают простые задачи на все арифметические действия; -решают составные задачи (не более 4 действия) на все арифметические действия, которые представляют собой различные комбинации простых задач; -понимают сущность алгебраического приема решения задач (с помощью составления уравнения)

Основу отбора и структуирования содержания, процессуальную харак- теристику изучения вопросов этой линии курса математики составляют следующие приоритетные концептуальные положения:

- задача - это особая форма познания, объект, детерминирующий процесс мышления человека, понимаемый как деятельность;

- в более узком понимании (на уровне начальных классов) задача – это спе- цифический вид математических упражнений, которые присущи такие су- щественные признаки как задание, предъявляемое с помощью текста на естественном языке, в содержании текста описывается житейская ситуация (ситуации), которая отражает количественные характеристики объектов и отношений между ними, в тексте содержится вопрос, ответ на вопрос получится в процессе выполнения арифметического действия (или арифметических действий);

- в узком понимании решить задачу означает раскрыть связи между данными и искомым, на основе чего выбрать, а затем выполнять действия и дать ответ на вопрос задачи или осуществить переход от конкретного содержания зада -чи к математической модели (числовое выражение и равенство, уравнение) – описанию ситуации на языке цифр и знаков (перевод естественного на мате- матический язык);

- задачи как средство обучения раскрывают значения и содержания математических понятий и как цель обучения формируют умения решать определенные ее типы;

- задачи, как и любые задания с математическим содержанием, в числе кото- рых примеры, занимательные, игровые и нестандартные задания образуют систему математических упражнений основного средства обучения учебника;

Особенности содержания образования линии курса математики «Задача и процесс ее решения» определяются номенклатурой понятий и способов действий, представленной в таблице.

Кл.-ы	Содержания линии курса математики «Задача и процесс ее решения»
1 кл.	Сравнение двух групп предметов (больше, меньше, столько же). Объединение и удаление. Задача и существенные ее признаки. Составные элементы задачи и эта- пы ее решения. Составление и решение простых задач на сложение, и вычитание (нахождение суммы и остатка; числа, больше или меньше на несколько единиц; разностное сравнение). Обратная задача. Взаимообратные задачи. Сравнение и преобразование задач в одно действие
2 кл.	Составление и решение задач на нахождение неизвестных слагаемых, уменьшае- мого и вычитаемого как задачи обратные задачам на нахождение суммы и остатка. Составление и решение простых взаимообратных задач на сложение и вычита- ние. Составление и решение задач в два действия (сложение, вычитание). Сравне- ние и преобразование задач в одно и два действия. Решение задач разными спосо- бами
3 кл.	Составление и решение простых задач на умножение, и деление (нахождение сум- мы одинаковых слагаемых, деление по содержанию и на равные части; нахожде- ние неизвестных множителей, делимого и делителя; нахождение числа, больше или меньше в несколько раз, на кратное сравнение; нахождение доли числа; на зависимости между величинами основных групп). Составление и решение простых взаимообратных задач на умножение и деление. Составление и решение задач в 2-3 действия на сложение и вычитание, умножение и деление. Сравнение и преобразование задач в 2-3 действия. Решение задач разными способами
4 кл.	Составление и решение простых задач, связанных с понятиями время, скорость и расстояние, с отношениями («больше на…», «меньше на…», «больше в…раз», «меньше в…раз»), выраженных в косвенной форме. Составление, решение, срав- нение и преобразование взаимообратных простых задач и задач в 3-4 действия. Решение задач разными способами, арифметическим и алгебраическим приемами

Особенности процессуальных характеристик технологии обучения решению задач в начальных классах заключается в формировании правильного представления о задаче и овладении умениями распознавать ее как разновидность математических заданий, отработки выполнения видов деятельности адекватные процессу решения задачи и создании условий по организации практики решения задач различными приемами и способами. Это обуславливает необходимость поэтапного рассмотрения материалов данной содержательно-методической линий курса математики.

Первый этап посвящается систематической подготовительной работе для введения задачи как особого вида математических упражнений, которая включает в себя:

- выполнение практической операции по объединению объектов в совокупность и удалению объектов из совокупности;

- сравнение двух групп предметов, по какому - либо признаку, которые способствуют раскрытию смысла сложения и вычитания, отношений (больше, меньше, столько же);

- составление суммы, разности по сюжету рисунка и поиск ответа на вопрос, соответствующий содержанию рисунка;

- приведение пояснений к изменению, изображенному на рисунке, которые приобщают к рассуждению, разбору и анализу ситуации

Второй этап начинается с введением термина задача и ознакомлением с ее структурными элементами, где:

- это осуществляется в наиболее оптимальный момент во всех отношениях, когда завершается обучение грамоте по учебнику «Букварь» и дети уже чи -тают за одну минуту текст, состоящий из 10-15 слов;

- термин задача вводится остенсивным способом, после чтения текста и диф- ференцируется ее условие и вопрос, т.е. выполняется первичный анализ,

- представление о задаче как особого вида математических упражнений фор- мируется в процессе сравнения двух заданий, где варьируются, существен -ные признаки понятия задача, которые способствуют распознаванию ее.

Далее рассматриваются в определенной последовательности решения основных видов простых задач:

- которые соответствуют последовательности изучения арифметических действий и отношений, так как они в процессе обучения решению задач выполняют аналогичные функции, какие выполняют при вычислениях таблицы сложения и умножения;

- отрабатывается на необходимом и достаточном уровне умения выбора и обоснования действия соответствующего содержанию простой задачи конкретного вида в отведенное время на его изучения в том или ином классе; - достижению такого результата, как правило, способствует использование сначала предметной иллюстрации при рассмотрении каждого нового вида простых задач;

- после чего осуществляется постепенный переход от использования конкретного вида наглядности к его абстрактному виду в последо- вательности предметная иллюстрация – схематическая иллюстрация – пере- вод на уровень представления ребенка – приведение образцов известных суждений – выполнение краткой записи задачи - ссылка на сформу- лированные общие правила – ориентация на текст (смысл опорных слов);

- причем динамика обучения решению задач в начальных классах харак- теризуется последовательностью, где результаты каждого предыдущего этапа является базой для последующего и практикуясь в нем закрепляется и развивается, так как, прежде всего, осуществляется подготовка к введению задач как особого вида математических упражнений и далее вводятся конкретные виды задач (задач в одно действие на сложение и вычитаниев, в два действия на сложение и вычитание, в одно действие на умножение и деление, в два-три действия на все арифметические действия, решение одной и той же задачи разными способами, задач в одно действие выраженные в косвенной форме и связанные с отношениями (больше и меньше на...;больше и меньше в...раз), задачи связанные с понятиями скорость, время и расстояние, решение задачи алгебраическим, арифметичесим приемами и отрабатываются соответствующие умения решать их);

- интегрируются такие виды деятельности как составление, решение, срав- нение и преобразование простых задач.

Здесь же начинается активное приобщение и акцентирование внимания учащихся на организацию и проведению систематической самостоятельной деятельности, адекватной каждому обязательному этапу процесса решения задачи:

- чтению текста ориентированного на достижение понимания в целом ситуации, описанной в задаче, ее условия и требования, всех терминов, знаков и символов, имеющихся в нем, что способствует отработке умения не только беглого чтения, но осознанного восприятия содержания задачи;

- поиску решения задачи,где осуществляется ее анализ, в ходе которого вычленяются условия и требования задачи, отношения между данными, между данными и искомыми, перефразировка текста, разбор задачи по тексту или по ее вспомогательной модели, выбор приема и способа решения задачи, обоснование выбора действия (действий и их последовательность), соответствующее тому или иному реальному отношению или ситуации, отраженных в ее содержании (или устанавливаются и обоснуются логическая последовательность выполняемых арифметических действий), который позволяют дать ответить на поставленный вопрос;

- реализации плана решения задачи, которая предполагает составление его устно или письменно, оформление решения задачи в одной из принятой форме, которое позволяет получить ответ на поставленный вопрос в задаче, иными словами сформулировать вывод о выполнении требований задачи.

- проверке решения задачи способствующей устраненять ошибки, если они имеются, выделить ответ задачи и сформулировать окончательный вывод о выполнении ее требований, осуществить при необходимости проверку, используя один из известных приемов (установление соответствия между ответом и условием задачи, решение задачи разными способами, составление и решение задачи, обратной данной и др).

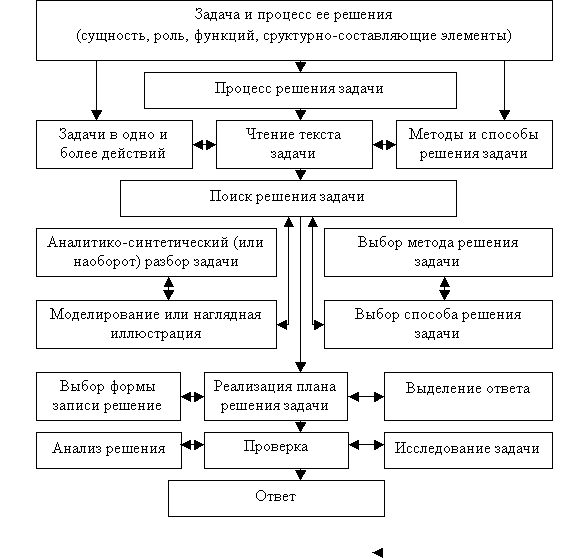
Связи элементов процесса решения задач представлены на блок-схеме.

Третий этап характеризуется введением задачи в два действия, которая состоит из двух простых задач. Этому предшествует целенаправленная подготовительная работа, которая включает следующие виды деятельности:

- решение простых задач и их сравнение;

- знакомство с выражением в два действия и с порядком выполнения действий в выражениях;

- преобразование заданий (без вопроса; недостающими данными; без вопроса и недостающими данными) в задачи в одно действие и решения их.

Самым ответственным моментом является введение понятия «состав -ная задача». Рассмотрение этого понятия предполагает актуализацию знаний необходимых для введения задач в два действия и установление существенного признака задачи в два действия и предполагает:

- рассмотрение двух задач, у которых решение одной есть условие другой;

- решение задачи и выполнение задания с недостающими данными, которое можно превратить в задачу, используя ответ решенной задачи;

- сравнение взаимообратных задач, одна из них данная, а две другие составляются из задания с недостающими данными, используя решение данной задачи;

- образование составной задачи из двух простых и решение ее;

- отработка умения по составлению и решению задач в два действия;

- сравнение и преобразование задач в одно и два действия;

- решение задач на сложение и вычитание разными способами.

Четвертый этап связан с введением:

- сначала простых, а затем составных задач на умножение и деление;

- рассмотрением составных задач (в два и более действия) на все арифметические действия, которые представляют собой различные комбинации простых ее видов.

Пятый условный этап характеризуется решением задач разными приемами (арифметическим и алгебраическим) и способами, при этом акцентируется внимание на следующее:

-считают, что задача решена разными способами; если при решении ее двумя способами последовательность арифметических действий и приводимые пояснения к ним по существу отличаются друг от друга;

- введение алгебраического метода решения задачи мотивируется его рациональностью по сравнению с арифметическим;

- при применении алгебраического метода решения задачи ответ на ее вопрос находят в результате составления и решения уравнений;

.- в зависимости от выбора неизвестного для обозначения буквой, от хода рассуждений можно составить различные по структуре уравнения по одной и той же задаче, что и свидетельствует о решения задачи различными алгебраичесескими способами.

Отработке деятельности соответствующей этапам процесса решения задач и в целом формированию умения способствует также планирование и проведение творческой работы в следующих направлениях: составление и решение задачи, обратной данной, составление задачи по известному решению и заданному отношению, по готовым схемам и рисункам, подбор условия к вопросу и наоборот, преобразование условий и вопроса задачи, преобразование задачи в одно действие, в два и более действий, использование результата измерения и дополнительных материалов для самостоятельного составления различных задач.

Использованная литература

1. Государственные стандарты начального образования республики Казахстан, -Алматы, республиканский издательский кабинет казахской академии образования им,Ы.Алтынсарина 1998г.

2. Государственные общеобязательные стандарты среднего общего образо- вания республики Казахстан. Начальное общее образование. –Алматы: РОНД,2002.

3. Программы для 1-4 классов по математике. –Алматы: РОНД, 2003.

4. Математика: Учебник для 1, 2, 3, 4 класса общеобразовательной школы /Т.К.Оспанов и др.–Алматы: Атамұра,1998 – 2009 гг.