Математика/5. Математическое моделирование

к.ф.-м.н. Тусупова С.А.

Университет «Туран», Республика Казахстан

Математическое моделирование собственных колебаний цилиндрических оболочек с конструктивными особенностями. Влияние радиального давления.

Эта задача в связи с применением тонкостенных сосудов в качестве топливных баков остается актуальной и до настоящего времени.

Исследованию влияния радиального давления на спектр собственных частот оболочки посвящен ряд работ.

В работах [2], [3] Бреславский, исходя из уравнений равновесия деформированного элемента оболочки, после ряда упрощений получил формулу для частоты колебаний при наличии гидростатического и всестороннего давления.

Рейсснер [9] на основе теории пологих оболочек, пренебрегая тангенциальными силами инерции, предложил более простое выражение для частоты колебаний при наличии нормального давления. Позже он рассмотрел и случай всестороннего давления [10], используя мембранную теорию пологих оболочек, но учитывая тангенциальные силы инерции. Однако, поскольку результаты Рейсснера в обоих случаях основаны на теории пологой оболочки, нельзя ожидать, чтобы они были справедливы и для мод колебаний, соответствующих малому числу окружных волн деформаций.

Экспериментальные исследования, относящиеся к данному вопросу, содержатся в работах [2, 6, 7, 8].

Рассмотрим уравнения частот, полученные на основе теории тонких оболочек.

Исходные дифференциальные уравнения колебаний в данном случае [4]:

,

, (1)

отличаются от приближенных уравнений

,

,

наличием в последнем уравнении члена .

При этом , (2)

где - давление, - окружное усилие.

Для краевых условий Навье система (1) приводится к уравнению частот, которое после упрощений принимает вид

(3)

Это выражение отличается от уравнения Бреславского [2]

(4)

множителем при и последним членом в знаменателе. Различие обусловлено несовпадением исходных уравнений и различными упрощениями при получении частотных уравнений.

Если на оболочку действует внешнее давление (), то исходя из (4) и полагая , можно найти значение критического давления, соответствующего потере устойчивости

(5)

Рейсснер [9] пришел к формуле

, (6)

которая может быть получена из формулы (4) для больших , когда имеют место следующие соотношения .

Значения собственных частот колебаний, вычисленных по уравнению (6), сопоставлялись с экспериментальными данными, полученными Готтенбергом [7]. Совпадение результатов, как видно из рисунка 1, оказывается достаточно хорошим даже для небольших значений n (m = 4). Это обстоятельство объясняется тем, что для исследовавшихся мод колебаний влияние осевых волн на частоту имеет большое значение, чем влияние окружных волн, и, следовательно, теория пологой оболочки дает очень хорошие результаты даже для мод с n = 2:3 (для n = 1 расчеты производились по балочной теории Тимошенко). Кроме того, движение, связанное с этими модами, является главным образом изгибным и поэтому осевые и тангенциальные силы инерции, которыми пренебрегает Рейсснер, оказывают на частоту незначительное влияние.

Однако, как следует из уточненных решений [1], осесимметричные моды и моды колебаний балочного типа для длинных осевых волн деформаций соответствуют значительным тангенциальным (при n = 1) и осевым (при n = 0) перемещениям. Поэтому пренебрежение продольными и тангенциальными силами инерции должно приводить к заметным неточностям. Более того, для этих мод колебаний гипотезы пологих оболочек некорректны, так что уравнение частот в форме Рейсснера (6) может содержать большую ошибку.

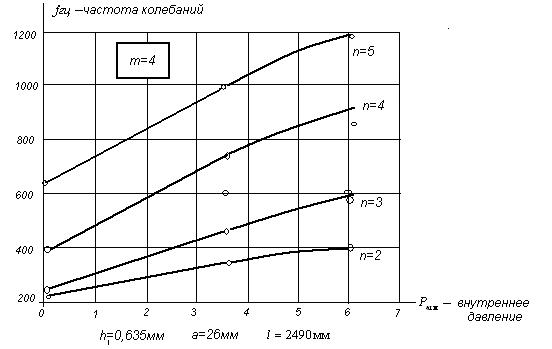
Рис. 1

Таким образом, уравнение (6) дает приемлемые результаты для мод колебаний с большим числом окружных волн. Если оно невелико, то уравнение пригодно лишь в тех случаях, когда длины осевых волн деформаций весьма малы по отношению к динам окружных волн.

В первом случае уравнение (6) с учетом упрощения Юаня принимает вид

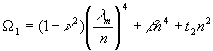. (7)

Для краевых условий, отличных от условий Навье, можно воспользоваться формулой (7), определяя в ней параметр по методу, предложенному Юанем [5]. Легко видеть, что влияние давления на собственные частоты колебаний оболочек при указанных предположениях не зависит от вида краевых условий.

Уравнение (3) можно представить в сокращенном виде

, (8)

где - параметр частоты ненапряженной оболочки (при ), - коэффициент влияния окружных усилий на частоту собственных колебаний оболочек, определяемый из равенства

. (9)

При действии на оболочку всестороннего давления в формуле (8) необходимо учесть наличие осевых усилий. Не нарушая общности исследования, можно положить

. (10)

Однако для резервуаров цилиндрической формы параметры и взаимосвязаны равенством .

Исходя из формул, полученных на основе теории тонких оболочек, можно сформулировать следующие выводы:

1. Наличие внутреннего давления приводит к увеличению собственных частот колебаний цилиндрической оболочки.

2. Внешнее давление снижает собственные частоты колебаний вплоть до , когда происходит потеря устойчивости оболочки.

3. Степень влияния окружных усилий на собственные частоты зависит от нескольких параметров и может быть оценена по выражению (9) для коэффициентов влияния .

4. Легко видеть, что влияние окружных усилий на собственные частоты возрастает при уменьшении относительной толщины оболочки. Таким образом, для очень тонких оболочек это влияние может быть весьма значительным.

5. Влияние окружных усилий на собственные частоты различных мод колебаний неодинаково.

6. Для осесимметричных колебаний (n = 0) давление не изменяет собственные частоты оболочки.

7. для колебаний балочного типа (n = 1) влияние окружных усилий становится заметным лишь у очень тонких и относительно коротких оболочек.

8. С увеличением числа окружных волн n степень влияния окружных усилий возрастает, достигая максимального значения при числе волн, соответствующем форме потери устойчивости под действием внешнего давления.

9. По этой причине минимальная частота при возрастании внутреннего давления соответствует модам с убывающим количеством окружных волн. Увеличение внешнего давления, наоборот, приводит к усложнению моды, соответствующей минимальной частоте.

10. Наличие внутреннего давления уменьшает плотность спектра собственных частот оболочки в области низких значений. Внешнее давление может приводить к существенному возрастанию плотности спектра для того же диапазона.

11. Окружные усилия не оказывают заметного влияния на внешние частоты и .

Литература:

1. Арменакас, Влияние начальных напряжений на колебания свободно опертых цилиндрических оболочек, Ракетная техника и космонавтика, 1964, № 9, с. 115-122.

2. Бреславский В.Е., Собственные колебания круговой цилиндрической оболочки, находящейся под действием гидростатического давления, Изв. АН СССР, ОТН, Механика и машиностроение, 1956, № 2.

3. Бреславский В.Е., Собственные колебания цилиндрических и конических оболочек, находящихся под давлением нормального давления. Тр. ХВАИВУ, 1957, в.65.

4. Никулин М.В., Собственные колебания цилиндрических оболочек, предварительно нагруженных крутящими моментами, Сб. «Прочность цилиндрических оболочек», ЦИАМ, 1959.

5. Юань, Колебания тонких цилиндрических оболочек конечной длины со свободно опертыми и защемленными краями. Сб. «Прочность цилиндрических оболочек», Оборонгиз, 1960.

6. Fung Y.C., Sechler E.E., Kaplan A., On the vibration of thin cylindrical shells under internal pressure, J. Aeronaut. Sci., 1957, V.24, # 9, p.650-660.

7. Gottenberg W.G., Experimental study of the vibration of circular cylindrical shells, J. Acoust. Soc. of Amer., 1960, V. 32, # 5, p.571-578.

8. Koval L.R., On the free vibration of thin clamped cylindrical shells, subject to radial pressure, J. Aero/ Space Sci., 1962, V. 29, # 5, p.615-616.

9. Reissner E., Non linear effects in vibrations of cylindrical shells, Aeromechanics Rept. AM 5-6, Ramo - Wooldridge Corp., 1955.

10. Reissner E., Note of vibrations of thin, pressured cylindrical shells, Aeromechanics Rept., AM 5-4, Ramo - Wooldridge Corp., 1955.