Математика/5. Математическое моделирование

G.G. Shvachych, М.А. Sobolenko

National metallurgical academy of Ukraine,Dnepropetrovsk, Ukraine

MATHEMATICAL DESIGN OF MUCH SEQUENCING MODE OF HEAT TREATMENT OF LONG GOOD

Introduction. Presently, for preparation metal to cold deformation spheroidizing and recrystallization annealing are used. This is conducted to achieve the purpose of increasing plasticity of the metal and removal of peening [1]. Heat treatment of metal is carried out in the stoves of mine type or bell-shafted stoves in a protective atmosphere. The deficiency of these traditional methods of preparation metal to cold deformation is heavy the considerable expenses of electric power and gas at annealing of metal in furnace, their low productivity, complication of providing the even heating and cooling of hanks of wire.

As the alternative for the indicated process of the furnace heating with electro-heat treatment is the method of heat treatment, the distinetive characteristics of which are high speeds of heating. In settings of the electro- contact heating treatment of metal is executed continuous-consistently, that allows to mechanize and automatize processes, quickly to pass to the new modes of heat treatment. For the terms of wiffetss production (production of wire) this circumstance is determining at creation of new technological processes [2].Complication of development of technological lines consists in the much cyclic technological process of treatment of metal (preparation of surface is cold deformation - heat treatment) from a purveyance to the receipt of the required size of wire. 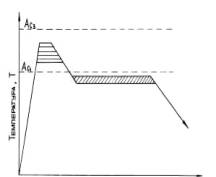For example, heat treatment in a technological process can be carried out on different charts (fig. 1 a, b) which depend on a brand became the set complex of properties.

Planning of such line requires implementation of difficult calculations and verification them in the experimental-industrial mode at the choice of construction of setting and descriptions of equipment, allowing to carry out the speed heating, following after him isothermal self-control with the subsequent speed cooling.

time, s time, s

а) b)

Fig.1. Harts of the spheroidizing annealing of wire with partial phase recrystallization and subsequent isothermal self-control (a) and mulch cyclic mode of heat treatment (b)

Development and use of mathematical model, characterizes the temperature field of metal in the process of heating, self-control and cooling will allow to get information which can be used for creation of equipment for the speed heating and cooling of long good.

Development of mathematical model. The interconnection of the thermal field with electromagnetic is conditioned that the sources of heat are determined from the decision of electromagnetic task. At the same time conductivity, dielectric and magnetic permeability of bodies depend on a temperature. These dependences can have both smooth and saltatory character. Character of these dependences influences at choice method of calculation. It is very important, that all affecting of the electromagnetic field properties of bodies and, in final analysis, on the coefficients of equalizations show up through the changes of temperature and are inertia. High-quality it is expressed in that thermal permanent time of the system and its parts much more electromagnetic permanent. Therefore thermal and electromagnetic tasks can be decided on certain temporal intervals independent of each other with the step correction of associate sizes. A division is conditional, because from the assumptions accepted at a calculation or from calculation features all methods are given by results with a certain error.

Thermal processes are described by Fure’s differential equalization that looks like [3]

(1)

where w – is volume closeness of internal sources of heat closeness of the material; - coefficients of heat capacity and heat conductivity accordingly.

If a transversal section of wire is small as compared to long, and coefficient of heat conductivity is considerable, in equalization (1) it is possible to put gradients of temperature on Y and Z equal to the zero. In this case a task reduses to mono measuring, when the overfall of temperature takes place only in the direction of longitudinal co-ordinate X. At such approach it is possible to take into account heat emission in the most differential equalization as a subzero source, and the interconnection of the thermal field with electromagnetic will be conditioned positive sources heats which are determined from the decision of electromagnetic task. Thus, the following differential equalization of heat conductivity is simplified :

(2)

where W – is amount of heat, conditioned converting of electromagnetic energy into thermal, or given unit of volume of bar in time unit in an environment in the mode of cooling. Thus, at the much cyclic mode a mathematical model (2) can describe the modes, allowing to carry out both warming self-control and cooling modes. For each of them the functional filling of source will be by it. In first case the function of W corresponds the selection of heat which can be appraised by Joule law. In the second case he can be presented as

(3)

where - is a coefficient of heat exchange, - relation of area of section of bar toward the perimeter of section ( - for a cylindrical bar, with radius R)

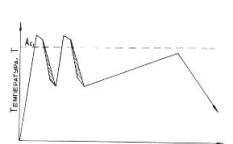
As in the much cyclic mode of heat treatment, presented on fig.2, added every cycle except for the sources, also moments of time and amplitude of temperatures, there is possibility of problem (2) definition, (3) as reverse. Under the structure of thermal model will understand a differential model (2), (3). The specific features of thermal model are such, that for all modes, reverse task, is the basic mean of receipt of necessary information at the decision of tasks of thermal design for the chart of production line.

In this work Reverse Task of Heat Conductivity decides by bringing it over to the extreme raising. In-use approach consists of that at the decision of RTHC the sought after causal descriptions of heat-exchange process are examined as parameters managements, included in the decisions of direct tasks [4].

The presented raising of task allows to decide a mathematical model (2) within the framework of one of perspective in a decision reverse tasks of heat exchange, proper their extreme raising with the use of the known numeral methods of theory of optimization.

The results of decision of reverse task on the developed approach are presented on a picture 2.

Conclusions

New approach is considered to the problem of the speed heating and cooling of long good in the technological stream of production of wire. The basic parameters of management the speed mode of heat treatment are got on the basis of decision of reverse task of heat conductivity, in which description of process examined as management parameters. The mathematical design of speed process of heating and cooling of long good showing efficiency offered approach.

Fig. 2. Much sequencing mode, including the rapid heating(1), self-control(2) and cooling(3)

Reference

1. Долженков И.Е., Долженков И.И. Сфероидизация карбидов в стали.-М.: Металлургия, 1984.- 143 с.

2. Колпак В.П., Лещенко А.Н., Полторацкий Л.М. Комплексные линии электротермической обработки стального проката и проволоки// Сборник докладов 4-ой Международной конференции “Оборудование и технологии ТОМ и сплавов”.- Харьков.- 2003.- С.42-44.

3. Немков В.С., Полеводов Б.С. Математическое моделирование на ЭВМ устройств высокочастотного нагрева. – Л.: Машиностроение, 1980. - 64 с.

4. Швачич Г.Г., Шмукин А.А., Протопопов Д.В. Некоторые особенности математического моделирования обратных задач исследования теплофизических свойств материалов// Металлургическая теплотехника. Сб. науч. трудов НМетАУ в 2-х книгах. Книга первая. – Днепропетровск: Пороги, 2005.- С.449-456.