Марзан С.А.

Брестский государственный университет имени А.С. Пушкина

Системы нелинейных дифференциальных уравнений с дробной производной Капуто в пространстве непрерывно-дифференцируемых функций

В связи с приложениями в теории интегральных и дифференциальных уравнений важной задачей является изучение свойств операторов дробного интегрирования и дифференцирования в различных функциональных пространствах. Достаточно полно разработаны такие вопросы для операторов дробного интегро-дифференцирования в классе интегрируемых функций [1, § 2] и весовом пространстве непрерывных функций [2], [3]. С использованием этих результатов, в работах [4]-[5] были исследованы краевые задачи для нелинейных дифференциальных уравнений с дробной производной Римана-Лиувилля в пространстве , а в работах [2], [3] – в пространстве .

Настоящая работа посвящена исследованию задачи Коши для системы нелинейных дифференциальных уравнений с дробными производными Капуто [6] в банаховом пространстве вида

, (1)

,

, .

Обозначим через модифицированную дробную производную, определяемую формулой

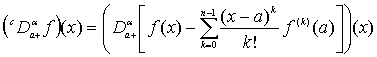, (2)

где – дробная производная Римана-Лиувилля [1] функции , заданной на , комплексного порядка (), , при , и при .

Исследуем задачу Коши для системы нелинейных дифференциальных уравнений дробного порядка

, , , ), (3)

с начальными условиями

(4)

в банаховом пространстве (1). Исследования основаны на равносильности задачи (3)-(4) и соответствующей системы нелинейных интегральных уравнений Вольтерра второго рода

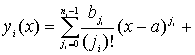
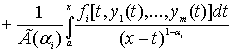
, (5)

и применении теоремы Банаха [7] для доказательства существования и единственности решения задачи Коши (3)-(4).

Теорема 1. Пусть , (, ), , . Пусть функции действуют из в R и таковы, что при любых и

. (6)

Для того, чтобы функции являлись решением задачи Коши (3)-(4), необходимо и достаточно, чтобы они являлись решением системы интегральных уравнений (5).

Доказательство теоремы проводится с использованием свойств дробных производных и интегралов Римана-Лиувилля [1].

Теорема 2. Пусть , , (,), . Пусть функции действуют из в R и таковы, что выполняются условия теоремы 1 и

.

Тогда существует единственное решение задачи Коши (3)-(4) в пространстве .

Литература:

1. Самко С.Г., Килбас А.А., Маричев О.И. Интегралы и производные дробного порядка и некоторые их приложения. – Минск: Наука и техника, 1987. – 687 с.

2. Килбас А.А., Бонилла Б., Трухилло Х. Дробные интегралы и производные, дифференциальные уравнения дробного порядка в весовых пространствах непрерывныхфункций // Доклады Нац. акад. наук Беларуси. – 2000. – Т. 44, № 6. – С. 18-22.

3. Kilbas A.A., Rivero M., Trujillo J.J. Existence and uniqueness theorems for differential equations of fractional order in weighted spaces of continuous functions // Fract. Calc. Appl. Anal. – 2003. – Vol. 6, № 4. – P. 363-399.

4. Kilbas A.A., Bonilla B., Trujillo J.J. Existence and uniqueness theorems for nonlinear fractional differential equations // Demonstratio Math. – 2000. – Vol. 33, № 3. – P. 583-602.

5. Килбас А.А., Бонилла Б., Трухилло Х. Нелинейные дифференциальные уравнения дробного порядка в пространстве интегрируемых функций // Доклады академии наук. – 2000. – Т. 374, № 4. – С. 445-449.

6. Caputo M. Linear model of dissipation whose Q is almost frequency independent // Geophis. J. Astronom. Soc. – 1967. – Vol. 13. – P. 529-539.

7. Антоневич А.Б., Радыно Я.В. Функциональный анализ и интегральные уравнения. – Минск: БГУ, 2003. – 430 с.