O. Semenova, A. Semenov, O. Wojciechowska

Vinnytsya National Technical University

Implementation of ternary logic operations

using two-threshold neurons

Artificial neural networks are physical cellular systems which can acquire, store and utilize experiential knowledge. They are considered as simplified mathematical models of brain – like systems and operate as parallel distributed computing networks. Implementation of binary AND, OR and NOT operations using threshold neurons has been described in [1]. The advantages of two-threshold neurons for fuzzy and ternary logic have been described in [2]. So, we propose to build up ternary minimum and maximum element as a neural network with linear and two-threshold neurons.

Principles and operations of ternary (three-valued) logic are described in [3]. So, let we have the ternary logic of [0,1,2]. Ternary minimum operation is performed so: .

Ternary maximum operation is performed so: .

Ternary inversion operation is performed so: .

For the linear-type neuron we have [1]:

, .

For the one-threshold type neuron we have [1]:

.

For the two-threshold type neuron we have [2]:

.

The neural network performing operation of ternary maximum is presented at fig. 1, where:

,

,

,

,

.

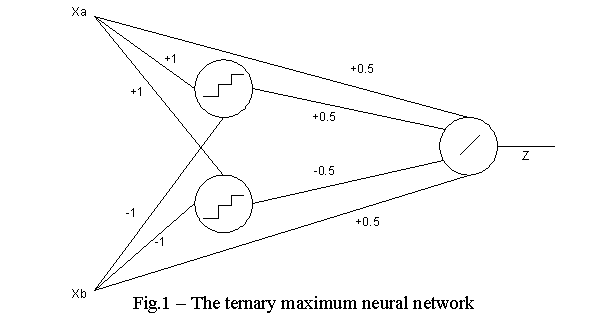
The neural network performing operation of ternary minimum is presented at fig. 2, where:

,

,

,

,

.

The neural network performing operation of ternary inversion is presented at fig. 3, where: , .

So, we have proposed three neural networks on linear and two-threshold neurons. The first operates as a ternary maximum element, the second does as a ternary minimum element, the third does as a ternary inversion element.

References

1. Neuronale Netze // www.iicm.edu/greis/node8.html.

2. Masahiro Sakamoto, Mititada Morisue. A study of ternary fuzzy processor using neural networks // Proc. of IEEE International Symposium on Circuits and Systems. – Hong Kong. – 1997. – pp. 613-616.

3. Ëûñèêîâ Á.Ã. Àðèôìåòè÷åñêèå è ëîãè÷åñêèå îñíîâû ÝÖÂÌ. – Ìèíñê: Âûøýéøàÿ øêîëà, 1974. -264ñ.