ФІЗИЧНИЙ ЗМІСТ ТЕОРЕМИ ОСТРОГРАДСЬКОГО-ГАУССА

Д.пед.н. Сусь Б.А., к.пед.н. ^*Мыслицкая Н.А.

Национальный технический университет Украины «Киевский политехнический институт», г.Киев, Украина

^*Винницкий государственный педагогический університет имени Михаила Коцюбинского, г.Винница, Украина

ФИЗИЧЕСКОЕ СОДЕРЖАНИЕ ТЕОРЕМЫ ОСТРОГРАДСКОГО-ГАУССА

В математике известна формула Остроградского, выражающая поток векторного поля через замкнутую поверхность как интеграл от дивергенции этого поля по объему, охваченному этой поверхностью:

$\iiint\limits_V\mathrm{div}\,\mathbf{F}\,dV=\iint\limits_S\!\!\!\!\!\!\!\!\!\!\!\subset\!\supset\;\mathbf F\cdot\mathbf{n}\,dS,$

Другими словами, интеграл от дивергенции векторного поля по некоторому объему равен потоку вектора через поверхность, ограничивающую данный объем. Формула применяется для преобразования объемного интеграла в интеграл вдоль замкнутой поверхности.

Общий метод преобразования тройного интеграла в поверхностный впервые применил Карл Фридрих Гаусс (1813, 1830) на примере задач по электростатике. В 1826 году М. В. Остроградский вывел формулу в общем виде, представив ее как теорему (опубликовано в 1831 году). Однако применение этой теоремы на практике оказывается некорректным. Рассмотрим это на примере расчета электрических полей, создаваемых электрическими зарядами.

Если электрический заряд q окружить замкнутой поверхностью S, то поток вектора напряженности через эту поверхность пропорционален величине заряда:

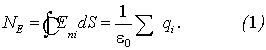
Иными словами, количество линий напряженности, которые исходят от заряда и пронизывают замкнутую поверхность, его окружающую, связано с зарядом, создающим эти линии. Очевидно, что к зарядам, которые замкнутой поверхностью не охватываются, теорема никакого отношения не имеет. Проблема в том, что традиционно теорема во всех учебных пособиях, как давних, так и современных, применяется не ко всем зарядам, которые создают электрическое поле, а лишь к небольшой части. Такое применение теоремы не соответствует ее содержанию, поэтому его нельзя считать корректным.

На рис. 1 приведены примеры применения теоремы Остроградского-Гаусса для расчета поля безграничной заряженной плоскости в учебных пособиях [1, 2, 3].

[1]

[2]

[3]

Рис. 1

Как видим, в приведенных случаях замкнутая поверхность окружает лишь часть заряда плоскости, тогда как поле создается всей безграничной заряженной плоскостью. Более того, к замкнутой поверхности, окружающей выделенный заряд Δq, теорема также применяется некорректно, так как считается, что поток вектора напряженности через боковую поверхность отсутствует (рис. 2).

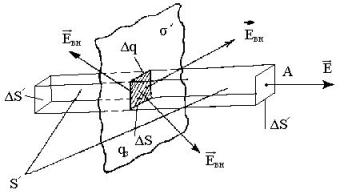
Рис. 2

Очевидно, что это не так, поскольку линии напряженности Е_вн поля, созданного зарядом Δq = σ ΔS , проходят через боковую поверхность и их поток через эту боковую поверхность не равен нулю, а наоборот - он значителен и им пренебрегать нельзя. Традиционно при применении теоремы пытаются учесть еще и заряд, который находится снаружи вспомогательной замкнутой поверхности (заряд всей плоскости за пределами вспомогательной замкнутой поверхности). Проблема в том, что этот внешний по отношению к гауссовой поверхности заряд также создает поле, причем в случае заряженной поверхности поле значительное. Но учесть это поле внешних зарядов с помощью теоремы Остроградского-Гаусса невозможно, потому что создаваемый ими поток всегда (т.е. тривиально) равен нулю, так как количество линий, входящих в замкнутую поверхность, равно количеству линий, которые выходят из нее. Таким образом, традиционная (подчеркнем - традиционная) запись теоремы имеет вид:

N_Е = N_Е_вн+ N_Евнеш = N_Е_вн + 0 = Δq/ ε₀. (2)

здесь N_Е_вн - поток напряженности поля , создаваемого зарядом Δq , который находится внутри замкнутой поверхности :

N_Евн= 2Е_внΔS' + E_вн. S'. ( 3 )

Из ( 2 ) и (3 ) имеем:

2Е_внΔS'+ E_вн. S' = Δq/ ε₀ . ( 4 )

Как видим, в данном случае традиционного подхода, последовательно используя теорему Остроградского-Гаусса, в принципе нельзя определить напряженность результирующего поля Е заряженной плоскости, поскольку это поле в формулу (4) не входит. Это результирующее поле создается не только зарядом Δq, который внутри вспомогательной поверхности, но также зарядом q_з, находящимся за пределами вспомогательной поверхности.

Для правильного применения теоремы при расчете поля заряженной плоскости или иного объекта необходимо замкнутой поверхностью охватить не часть, а весь заряд, который создает поле.

Если поле в некоторой точке A создается безграничной заряженной плоскостью S, то согласно физическому смыслу теоремы Остроградского-Гаусса весь заряд плоскости S необходимо охватить вспомогательной замкнутой поверхностью (рис. 3).

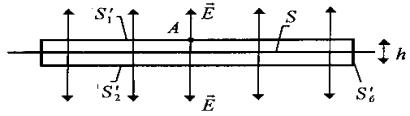
Рис . 3

Однако, реально нет необходимости выбирать вспомогательную поверхность S' бесконечно большой и охватывать ею весь заряд безграничной плоскости. Физически термин "безграничная заряженная плоскость" означает, что ее протяженность должна быть настолько большой, чтобы полем в точке A, созданным зарядами, которые находятся на краях плоскости, можно было пренебречь. Поэтому будем выбирать вспомогательную поверхность S' = просто большой. А боковую часть замкнутой поверхности высотой h, наоборот, возьмем малой, так чтобы потоком вектора напряженности через нее можно было пренебречь:

(5)

Согласно теореме Остроградского-Гаусса (1) этот поток равен:

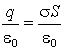=. ( 6 )

Учитывая (6), выражение (5) можно записать :

= ,

откуда поле заряженной плоскости

E = . (7 )

Аналогично рассчитывается поле заряженного цилиндра.

На данном примере применения теоремы Остроградского-Гаусса для расчета поля заряженной плоскости мы показали, как можно проблемно подойти к рассмотрению классического традиционного учебного вопроса, обратив внимание на правильную формулировку теоремы. Такой анализ, критическое отношение к учебному материалу акцентирует внимание на проблеме, вызывает интерес и стимулирует развитие мысли, что способствует не только усвоению учебного материала, но и формирует исследовательские навыки.

Выводы. Развитие критического мышления является важным для становления студента как будущего специалиста и формирования его компетентности. Создание проблемных ситуаций дает возможность привлечь студентов к творческой исследовательской деятельности. Рассмотрение физического смысла теоремы Остроградского-Гаусса и ее применения для расчета электрических полей позволяет активизировать учебную деятельность студентов.

Литература

1. Фейнман Р. Фейнмановские лекции по физике, т.5 / Р.Фейнман, Р. Лейтон, М. Сэндс. – М.: МИР. 1966. – С. 97.

2. Кингсеп А.С. Основы физики, т. 1. /А.С. Кингсеп, Г.Р. Локшин, О.А. Ольхов. – Москва: ФИЗМАТЛИТ. 2007. – С. 200.

3. Бутиков Е.И. Физика. Книга 2. Электродинамика / Е.И. Бутиков, А.С. Кондратьев. Физика. – Москва: ФИЗМАТЛИТ. 2008. – С. 28.