Òåõíè÷åñêèå íàóêè/11. Ðîáîòîòåõíèêà
cand. tech. sci. Semakhin A.M.
Kurgan State University,
Russia
THE
MATHEMATICAL DESCRIPTION OF THE TRAJECTORY OF MOVING GRIPPING DEVICE OF
INDUSTRIAL ROBOT
The analysis of
production of the enterprises of mechanical engineering and instrument making
with small-scale type of manufacture has shown, that time of processing of a
detail makes no more than 10 % from time of manufacturing. The rest of the time
is necessary on processes of loading-unloading, moving and storage /1/.
Reduction of
auxiliary time is a topical problem.
The industrial
system in structure of the numerically controlled machine tool, the industrial
robot for loading-unloading of the basic process equipment, work-storage unit
and workpiece storage is investigated. It is necessary to develop the
mathematical description and to execute calculation of a trajectory of moving gripping
device of the industrial robot in view of obstacles of a working zone of the NC
machine tool.
For the description
of movement gripping device of the industrial robot in base system of
coordinates representation Denavit-Hartenberg, consisting in formation of a
homogeneous matrix of transformation is used. It allows to transform
consistently coordinates of gripper from the system of readout connected with
last link, to base system of coordinates /2/.
The homogeneous
matrixes of transformation connecting i and i-1 look like system of
coordinates.
For a rotary joint
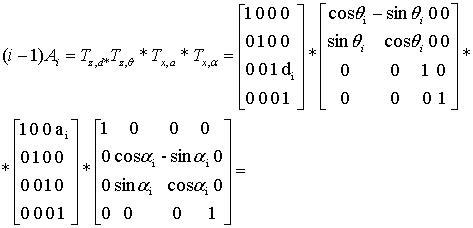
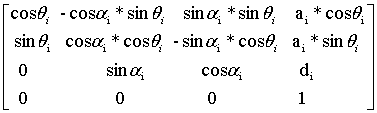(1)
For a forward joint
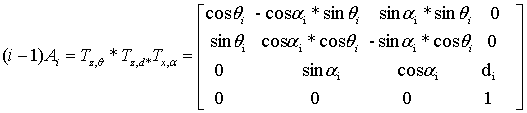(2)
where 
- a homogeneous matrix of
elementary turn of axis 
on corner 
.
- homogeneous matrix of shift
along axis 
on distance 
.
- homogeneous matrix of
elementary shift along axis 
on distance 
.
- homogeneous matrix of
elementary turn around of axis 
on corner 
.
For transition from 
systems of coordinates to 
expression is fair
(3)
where 
- radius-vector of the point set
in system of coordinates 
of a part, 
.
- matrix of transformation 
of a link.
As any point 
it is accepted the material
point 
, expressing gripping device of the industrial robot.
Let's consider a trajectory of movement of material point 
during the initial moment of
time 
. Process of transition of system of coordinates 
in system of coordinates 
is expressed in the form of the
equation
(4)
where 
- product of matrixes of transformation
from the previous link to the subsequent link, since 0 link and finishing n link.
- radius-vector of a point n à link.
Differentiating the equation 4 on 
, we receive the general differential equation describing possible
trajectories of moving the gripper of the industrial robot with a detail
concerning coordinate system 
.
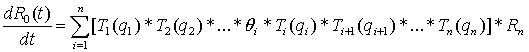(5)
where 
- the radius-vector defining
position of a point 
.
For rotary and forward pairs
; 
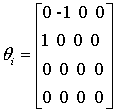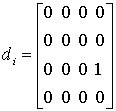(6)
The equation 5 is the generalized differential equation describing a
trajectory of movement gripping device of industrial robot.
For maintenance of a unobstructed conclusion gripping device of
industrial robot from a zone of loading of the basic process equipment the
determinant pays off /3/.
(7)
where 
- determinant of private
derivatives 
and 
on X, Y.
- determinant of private
derivatives 
and 
on Y, Z.
- determinant of private
derivatives 
and 
on Z, X.
The determinant 
is calculated under the formula
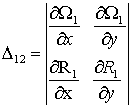(8)
where 
,
- private derivatives 
on X, Y. 
: 
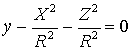- surface of safety (elliptic
paraboloid) zone of loading of the NC machine tool.
, 
- private derivatives 
on X, Y. 
: 
- the guiding plane.
If determinant 
industrial robot cannot deduce
gripping device with a detail from a zone of loading of the NC machine tool on
a curve received by crossing 
and 
. At 
it is impossible to work out the
differential equation which decision coincides with crossing 
and 
. If determinant 
gripping device can move on
crossing surfaces 
and 
.
The differential equation of a curve on which
moves the gripping device of industrial robot looks like
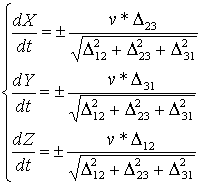(9)
The Cauchy problem is solved for definition
of the trajectory of moving gripping device of industrial robot. The Cauchy
problem is solved by Runge-Kutta method of the fourth order.
References:
1. V.A.Egorov,
V.D.Luzanov, S.M.Shcherbakov Transport store systems for flexible manufacturing
systems. - L.: Mechanical engineering, 1989. - 293 p.
2. K. S. Fu, R.C.
Gonzalez, C. S. G. Lee Robotics: Control, Sensing, Vision and Intelligence. –M.
Mir, 1989. – 624 c.
3. Pulatov S.I., Madrahimov
Z.T. Models and methods of functional-parametrical interaction of the
industrial robot with the processing equipment in structure of flexible
manufacturing systems. - Tashkent, 1990. - 50 p.