Технические науки/6. Механика

ГАВЕЛЯ Г.М.

Днепропетровский национальный университет им. О.Гончара

Неосесимметричная деформация нетонких

цилиндрических оболочек

Исследуется поведение толстостенной цилиндрической оболочки, нагруженной внешним давление по области , при упругопластическом деформировании. Для описания упругопластического поведения материала используется деформационная теория пластичности. При использовании метода дополнительных деформаций о равенстве усилий в расчетном упругом и пластически деформированном теле для расчетного упругого тела формулируется функционал, условиями стационарности которого будут являться уравнения равновесия в перемещениях для расчетного упругого тела при нагружении его действительной нагрузкой и фиктивной от дополнительных деформаций. Такой подход вполне обоснован, так как рассматривается активное нагружение оболочки при неизменном характере действующей нагрузки. Из предположений деформационной теории следует, что

, (1)

где – упругая и пластическая части деформации соответственно . Процесс разгрузки считается упругим. Основные соотношения содержат неизвестные функции , которые будут определяться с помощью метода дополнительных деформаций [2].

С помощью вариационного метода решение поставленной нелинейной краевой задачи может быть получено как точка стационарности функционала, который, с учетом того, что , имеет вид:

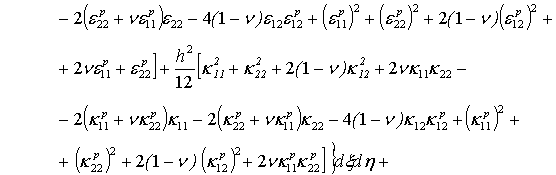
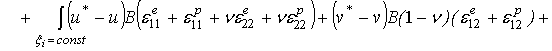(2)

,

, , ,

, , ,

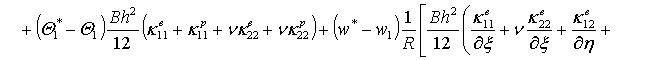
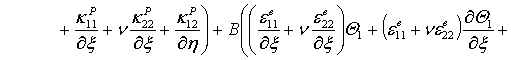
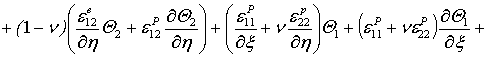
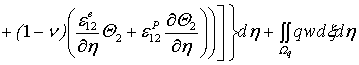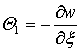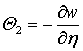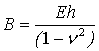где – продольное, окружное и радиальное перемещения точек срединной поверхности; – длина, радиус и толщина оболочки; – модули упругости и Пуассона соответственно, – область, занимаемая оболочкой.

Функции перемещений вдоль направляющей оболочки представим кусочно-полиномиальной аппроксимацией. Для этого направляющую оболочки нужно разбить на элементов узлами и в каждом узле ввести в рассмотрение значения искомых функций и их частных производных по продольной координате:

, , . (3)

Любая из функций на интервале между -тым и -м узлами аппроксимируется выражением

(4)

В качестве функций используются итерационные полиномы Эрмита третьей степени первого порядка [1]. Благодаря свойствам полиномов Эрмита аппроксимирующее выражение (4) принимает в -том узле значение , а его производная – значение производной по от функции . Такое представление обеспечивает непрерывность искомых функций и их первых производных в направлении оси . Из условия стационарности функционала (2) можно получить уравнение Эйлера для функций :

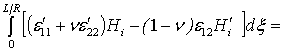
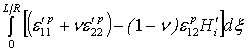, (5)

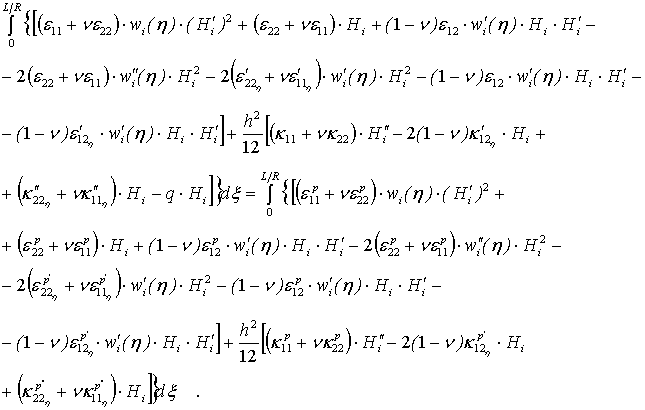
Внеинтегральные члены в функционале (3) равны нулю вследствие выполнения условий (3)–(4).

Систему (5) можно разрешить относительно производных от искомых функций, дополняя граничными условиями по координате . В качестве таких условий можно взять условие периодичности по окружной координате или условия симметрии.

Полученная краевая задача сводилась к задаче Коши при помощи метода Ньютона; для нахождения особых точек использовался алгоритм, позволяющий фиксировать точки ветвления решений в процессе движения по параметру нагрузки [1].

На каждом шаге метода Ньютона определяются пластические деформации . В используемом методе дополнительных деформаций пластическая часть деформации и принимается в качестве дополнительной деформации. С достаточной точностью можно принять [2]

, (6)

где – секущий модуль обобщенной кривой деформирования.

Решение задачи упругости при заданных внешних нагрузках и дополнительных деформациях , которые определяются формулой (6), совпадают с решением задачи деформационной теории пластичности. Метод дополнительных деформаций заключается в том, что за начальное приближение принимается , т.е. решается упругая задача и определяются и интенсивности деформаций . Определив по кривой деформирования новое значения напряжений и новый секущий модуль , можно определить по формуле (9) дополнительные деформации первого приближения

. (7)

Таким образом, дополнительные деформации -го приближения определяются через деформации , найденные из решения упругой задачи предыдущего приближения с дополнительными деформациями .

С помощью изложенного алгоритма рассматривалась оболочка под действием равномерного внешнего давления, приложенное по полосе с углом раствора . На рис.1 представлена сравнительная зависимость критического значения нагрузки ( отнесено к равномерно нагруженной оболочки) для оболочки с геометрическими параметрами, , и шарнирном опирании торцев от угла в первом случае нагружения при учете пластических деформаций (кривая 2) и без них (кривая 1).

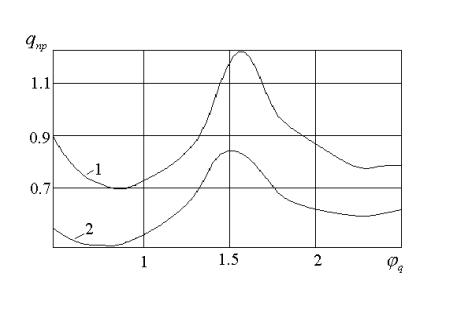
Рис. 1

Литература:

1. Андреев Л.В. Устойчивость оболочек при неосесимметричной деформации // Л.В. Андреев, Н.И. Ободан, А.Г. Лебедев. М.: Наука, 1988. – 208с.

2. Биргер И.А. Метод дополнительных деформаций в задачах теории пластичности. Изв. АНУССР. ОТН. Механика и машиностроение, 1963. – №1.– с. 47-56.