Технические науки/6. Электротехника и радиоэлектроника

Гулина И.Г. , Обора И. О.

ГВУЗ «Национальный горный университет», Украина

Разработка методов прогнозирования ARTCP протокола по скважности с целью повышения пропускной способности.

В протоколе ARTCP полностью переработаны все механизмы управления потоком. Механизм коррекции ошибок передачи в ARTCP не влияет на скорость передачи. От TCP сохранены оконный механизм для управления загрузкой получателя, алгоритмы определения RTT и установки таймера ТПП. Признаком потери сегмента служит срабатывание ТПП или приход двух последовательных подтверждений одного сегмента. Алгоритм управления скоростью включает в себя: функции диспетчеризации сегментов, измерения скорости и адаптации скорости (рис. 1).

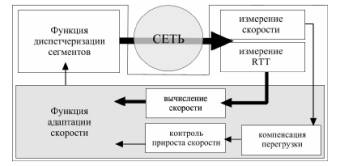
Рис. 1. Функциональная схема механизма управления потоком ARTCP

Основным методом анализа коммуникационных сетей является теория систем массового обслуживания. Однако большинство результатов этой теории получено в предположении о конечности дисперсий как интервалов между поступлениями сегментов, так и длительностей их обслуживания. Экспериментальное изучение трафика в TCP/IP сетях (В. Леланд и др.) показало, что такое предположение о конечности дисперсии неверно. В классических работах В. Виллингера и М. Таггу показано, что трафик в сетях архитектуры TCP/IP обладают свойством самоподобия.

Для определения того, обладает ли трафик свойством самоподобия, обычно вычисляется коэффициент Хёрста. Целью данного сценария является выявление свойства самоподобия ARTCP трафика.

Топология:

Топологическая схема эксперимента представлена на рис.2. Согласно схеме через территориальную сеть проходит трафик между двумя ЛВС - по 10 узлов в каждой. Данные снимаются с маршрутизатора R1. ПС каналов WAN составляет 512 Кб/с.

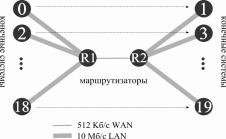
Рис. 2. Топологическая схема 10, с 20-ю парами источник-получатель

Эксперимент:

Для вычисления коэффициента Хёрста ARTCP трафика, был проведен модельный эксперимент, результатом которого явилась серия из 147036 измерений, суммирующих события прихода сегментов с данными на маршрутизатор R1 от 10-и активных источников за периоды 0.1 с. Время моделирования составило 19174 с, а общее число событий поступления сегментов с данными в маршрутизатор R1: 1208031.

График фрагмента (9000-12000 с) исходной серии измерений приведен на рис.3, а на рис.4 изображен результат сглаживания фрагмента последовательным применением wavelet symlet8 декомпозиции уровня 10, отбрасывания коэффициентов разложения превышающих 150 и восстановления сигнала. Для wavelet анализ применялась программа Matlab.

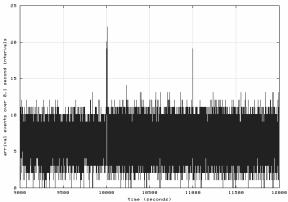
Рис. 3. Фрагмент полученной серии измерений.

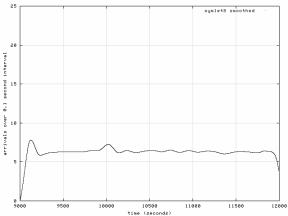
Рис. 4. Фрагмент серии измерений после сглаживания с применением sym8 wavelet

Полученная исходная серия подверглась статистической обработке с применением методов R/S статистики (рис.5) и aggregatedvariance (рис.6). По результатам применения обоих методов был вычислен коэффициент Хёрста: по методу R/S он равен 0.63, по методу aggregatedvariance: 0.65.

Для этого мною были разработаны программы на языкеС, выполняющие вычисления по методам R/S и AVM достаточно быстро. Линейная аппроксимация по методу наименьших _{квадратов производилась с помощью программы статистического анализа PSPP21.}

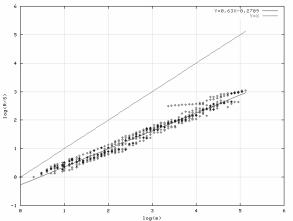
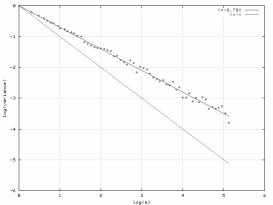Рис. 5. результат применения метода Rescaledadjustedrange (R/S)

Рис.6. Результат применения метода aggregatedvariance

Выводы:

Таким образом, трафик ARTCP, как и другой сетевой трафик по Вилингеру и Таггу, обладает свойством самоподобия. Использование метода имитационного моделирования протокола ARTCP является в настоящий момент единственно возможным средством его исследования.

Наличие свойства самоподобия у трафика, полученного на имитационной модели, так же как и у трафика реальных сетей, указывает на то, что разработанная модель хорошо воспроизводит процессы, происходящие в реальных сетях.

Литература:

1. Гольдштейн Б. Протоколы сети доступа. – М.: Радио и связь.– 1999.– 623 с.

2. Бертсекас Д., Галлагер Р. Сети передачи данных. Пер. с англ. М.: Мир. 1989. – 365 с.

3. Протоколы сети доступа. Том 2: Б. С. Гольдштейн — Санкт-Петербург, 2005. – 288 с.