Современные информационные технологии/4. Информационная безопасность

Юдін О.К., д.т.н., проф.

Курінь К.О.

Національний авіаційний університет, Україна

МЕТОД СТРУКТУРНОГО КОДУВАННЯ ДВІЙКОВИХ ПОСЛІДОВНОСТЕЙ

У зв’язку з тенденцією постійного інтенсивного розвитку комп'ютерної графіки бурхливо розвивається певна область теорії компресії – методи стиснення зображень.

Більшість сучасних методів стиснення спираються на статистичне кодування даних. Останнім часом в теорії інформації з’явилися нові нестатистичні підходи до оцінки кількості інформації для процедур стиснення. Це зумовлено тим, що при використанні статистичних методів для стиску інформації, досягнути коефіцієнта стиску без втрат більш ніж 1,7-2,2 для реалістичних зображень важко.

Тому метою даного дослідження є розробка методу кодування, який використовує принципово відмінні від статистичних характеристики інформаційного повідомлення, з урахуванням можливості його подальшого використання в технології стиснення зображень.

Серед сукупності технологій компактного представлення даних виділяють новий клас методів стиснення, заснований на усуненні структурної надмірності шляхом виявлення структурних закономірностей в двійкових послідовностях за визначеними ознаками – методи структурного кодування.

Методи структурного кодування для підвищення ступеня|міри| стиснення при умові одночасного збереження|зберігання| заданої якості відтворюваного зображення, повинні забезпечувати дотримання наступних|слідуючим| вимог [3]:

1. обробці піддаються двійкові дані, оскільки двійкове представлення|вистава| є|з'являється| універсальним для представлення інформації від різних джерел;

2. процес стиснення даних організовується на основі усунення структурної надмірності;

3. в процесі стиснення враховуються структурні закономірності одночасно по декільком визначеним ознакам; при цьому для забезпечення збільшення ступеня стиснення ознаки мають бути взаємозалежними.

Розглянемо такі структурні ознаки двійкових послідовностей: кількість переходів від одиничного елемента до нульового та кількість переходів від нульового елемента до одиничного . В таблиці 1 наведені двійкові послідовності довжиною в 4 біти. Для кожної з послідовностей вказані значення структурних ознак та . Зазначимо, що аналіз значень структурних ознак ведеться з урахуванням того, що в двійкову послідовність вводиться додатковий нульовий розряд (в таблиці виділений сірим). Таку послідовність називатимемо розширеною.

Очевидно, що двійкові послідовності, які характеризуються однаковими значеннями структурних ознак, можна згрупувати в структурні групи. В таблиці 1 структурні групи (СГ) виділені різними відтінками сірого.

Таблиця 1

Значення порядкових номерів та структурних ознак для двійкових послідовностей довжиною біти

Номер з/п	Двійкова послідовність	Структурні ознаки		Номер структурної групи	Порядковий номер в СГ
0	00000	0	0	0	0
1	00001	1	0	1	0
2	00010	1	1	2	0
3	00011	1	0	1	1
4	00100	1	1	2	1
5	00101	2	1	3	0
6	00110	1	1	2	2
7	00111	1	0	1	2
8	01000	1	1	2	3
9	01001	2	1	3	1
10	01010	2	2	4	0
11	01011	2	1	3	2
12	01100	1	1	2	4
13	01101	2	1	3	3
14	01110	1	1	2	5
15	01111	1	0	1	3

Разом з тим комбінація та однозначно визначає ще одну ознаку, яка характеризує двійкову послідовність – номер структурної групи . Параметр також визначає загальну кількість переходів між нулем та одиницею в послідовності. При чому значення , та зв’язують наступні співвідношення:

При цьому кодування полягатиме в привласнені послідовності її порядкового номера у даній групі. Значення порядкового номера буде меншим за десяткове значення двійкової послідовності. На основі визначеного підходу буде забезпечуватися подальша процедура стиснення.

Порядковий номер для двійкової послідовності довжиною біт згідно значенню структурної ознаки розраховується за формулою:

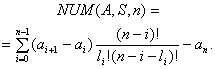
Тут - кількість залишкових переходів між нульовими та одиничними елементами двійкової послідовності при обробці переходу між та , яка чисельно дорівнює:

Таким чином, обґрунтовано процедуру кодування даних та доцільність використання структурних ознак в задачах стиснення інформаційних потоків.

Найбільший ступінь стиснення досягатиметься, коли двійкова послідовність довжиною кодуватиметься порядковим номером 0 або 1, для представлення яких необхідний лише один біт. Чисельно значення максимального ступеня стиснення дорівнюватиме:

Найменший ступінь стиснення буде отриманий в тому випадку, якщо двійкова послідовність кодуватиметься значенням найбільшого можливого біноміального коефіцієнту для заданої довжини двійкової послідовності, зменшеним на 1 (врахуємо, що нумерація послідовностей в структурній групі починається з 0). При цьому значення біноміального коефіцієнту складе:

.

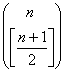Тут операція позначає взяття цілої частини від дробового числа.

Чисельно значення найменшого ступеня стиснення дорівнюватиме:

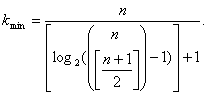
В таблиці 2 наведені значення ступенів стиснення та для двійкових послідовностей різної довжини.

Таблиця 2

Значення максимального та мінімального ступенів стиснення для двійкових послідовностей різної довжини

Довжина двійкової послідовності , біт	Максимальній коефіцієнт стиснення	Мінімальний коефіцієнт стиснення
4	4	1,333
8	8	1,143
16	16	1,143
32	32	1,067
64	64	1,049

Отримані результати дозволяють зробити висновок про доцільність подальшого використання запропоновано методу кодування двійкових даних в технологіях стиснення.

Список використаної літератури

1. Урсул А.Д. Нестатистические подходы в теории информации / А.Д. Урсул // Вопросы кибернетики.–1967.–№2.– С. 88–93.

2. Шеннон К. Работы по теории информации и кибернетике / К. Шеннон - М.: Изд – во иностр. лит – ры, 1963. – 793 с.

3. Юдін. О.К. Методи структурного кодування даних в автоматизованих системах управління / О.К. Юдін – К.: НАУ, 2007.