Горлатов
А.С.
ФГОУ ВПО «Калининградский государственный
технический университет», Россия
ОБОСНОВАНИЕ РАЗМЕРНОЙ ЦЕПИ МАШИНЫ ДЛЯ НАПОЛНЕНИЯ БАНОК ПРОДУКТОМ
Жгутоформующие
дозировочно-наполнительные машины с прямой передачей доз продукта из рыбовода
(жгутообразователя) в банки позволяют значительно повысить эффективность
операций наполнения банок рыбой [1-4]. Машины карусельного типа, реализующие
такой процесс, способны обеспечить заданную производительность без изменения
интенсивности непосредственно процесса наполнения. Эти достоинства открывают
возможность успешного использования карусельных наполнительных машин с прямой
передачей доз в автоматизированных рыбоконсервных линиях.
Характерной
особенностью карусельных жгутоформующих машин является наличие верхней и нижней
заслонок, занимающих независимое положение относительно карусели, вращающейся
вместе с рыбоводами [4]. При работе машины формируемая доза продукта
контактирует с опорной поверхностью нижней заслонки в течение большей части
периода кинематического цикла карусели. Это сопровождается
"размазыванием" некоторой массы дозы по рабочим поверхностям,
приводит к потере продукта и не способствует точности дозирования по массе. Для
устранения недостатков предложена соответствующая конструктивная разработка
[5].
Целью
статьи является математическое обоснование размерной цепи разработанного
устройства и точности его функционирования.
На
рис. 1 предоставлена принципиальная схема технологической карусели (в плане) с
обозначением основных конструктивных элементов. Данные, необходимые для расчета
параметрических характеристик анализируемого устройства, содержит схема на рис.
2. Здесь OO1=l1 - расстояние между осями вращения карусели и качания коромысла; O1B=l2 - расстоянии от оси качания коромысла до центра заслонки; OC=l3 - расстояние от центра вращения карусели до начальной точки рабочего
профиля неподвижного копира; β -
угол поворота коромысла, несущего заслонку, при котором последняя полностью
освобождает выходное сечение мерного стакана; φ - угол поворота карусели, которому соответствует поворот
коромысла с заслонкой на угол β.

Позиции: 1 – карусель, 2 – стакан
мерный, 3 – заслонка поворотная,
4 –
коромысло, 5 – копир неподвижный
Рис. 1. Схема карусели наполнительной машины
При
работе наполнительной машины заслонка 3 перекрывает выходное сечение мерного
стакана 2 в течение времени формирования дозы и последующего отрезания её от
жгута. В момент окончания реза ролик коромысла 4 входит в контакт с рабочим
профилем неподвижного копира 5. При этом, поскольку коромысло шарнирно связано
с каруселью 1, ему сообщается сложное движение в направлении, противоположном
вращению карусели. После поворота коромысла на угол β заслонка полностью освобождает выходное сечение мерного
стакана. Далее следует передача дозы продукта из мерного стакана в банку. В
процессе передачи дозы коромысло занимает относительно карусели фиксированное
положение, поэтому угол β не
изменяется. Возвращение заслонки в исходное положение (под стакан)
обеспечивается действием пружины при движении ролика коромысла по
соответствующему участку профиля неподвижного копира. Положение заслонки под
мерным стаканом фиксируется силовым влиянием на коромысло пружины и упора.

![]()
![]() - заслонка в момент начала ее движения относительно карусели;
- заслонка в момент начала ее движения относительно карусели;
![]() - заслонка после поворота коромысла на угол b;
- заслонка после поворота коромысла на угол b;
- мерный стакан в положении без
заслонки
Рис. 2. Схема к расчету углов b, g, j
Найдем
зависимость для определения угла β.
Из схемы на рис. 2 получим 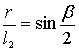 ,
, 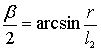 или
или
 ,
(1)
,
(1)
где r – радиус заслонки.
В
табл. 1 приведены значения углов β, полученные при постоянных значениях
диаметров заслонок и l2 = var.
Графики,
построенные по данным табл. 1, представлены на рис. 3.
Таблица 1. Углы размаха
заслонок, град
|
l2, мм |
Диаметр заслонки d, мм |
||
|
52 |
78 |
106 |
|
|
200 |
14.940 |
22.490 |
30.734 |
|
250 |
11.940 |
17.950 |
24.480 |
|
300 |
9.944 |
14.940 |
20.351 |
|
350 |
8.520 |
12.794 |
17.420 |
|
400 |
7.454 |
11.940 |
15.230 |
|
450 |
6.624 |
9.944 |
13.530 |
|
500 |
5.961 |
8.950 |
12.170 |

При значениях d = const, mm: 1 – 52, 2 –
78, 3 – 106
Рис. 3. Графики функций b = f(r, L2)
Анализ
графиков на рис. 3 показывает, что увеличение аргумента l2 при d = 2r = const, как и уменьшение d при l2 = const, сопровождается уменьшением угла β.
Освобождение
выходного сечения мерного стакана является результатом двух движений: сложного
движения коромысла, несущего заслонку, и движения мерного стакана вместе с
каруселью. Сложение этих движений ускоряет процесс освобождения сечения для
прохода дозы в банку. Поэтому угол φ
поворота карусели, при котором коромысло с заслонкой совершает поворот на угол β, является важной характеристикой анализируемого устройства,
подлежащей вычислению.
Из треугольника OO1C на рис. 2 получим ![]() ;
; ![]() или
или
![]() . (2)
. (2)
Для
нахождения искомого угла φ по
формуле (2) необходимо предварительно вычислить неизвестный угол γ, определяемый размерной цепью
устройства.
По
теореме синусов из треугольника OO1C на рис. 2 будем иметь  ;
;  ;
;  или
или
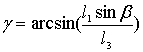 . (3)
. (3)
Следовательно,
угол поворота карусели, при котором заслонка полностью освобождает выходное
сечение мерного стакана, равен
![]()
 .
(4)
.
(4)
Из
выражения (4) следует, что при β
= const угол φ
поворота карусели зависит от значения параметров l1 и l3, которые неравнозначно влияют на величину
угла. В табл. 2 приведены значения угла φ,
полученные при постоянных значениях величин β
и l1 и варьировании l3.
Таблица 2. Угол φ поворота карусели, град
|
l3, мм |
Длина l1, мм |
||
|
400 |
550 |
700 |
|
|
436 |
2.696 |
|
|
|
454 |
3.862 |
||
|
472 |
4.930 |
||
|
490 |
5.910 |
||
|
508 |
6.815 |
||
|
586 |
|
2.012 |
|
|
604 |
2.916 |
||
|
622 |
3.760 |
||
|
640 |
4.552 |
||
|
658 |
5.296 |
||
|
736 |
|
1.605 |
|
|
754 |
2.342 |
||
|
772 |
3.040 |
||
|
790 |
3.702 |
||
|
808 |
4.331 |
||
Графики,
построенные по данным табл. 2, представлены на рис. 4.
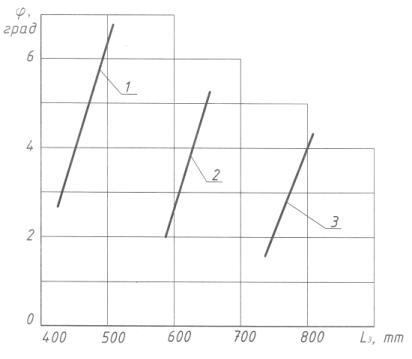
При значениях: b = 30, L1 = const, mm: 1 – 400, 2 – 550, 3 – 700
Рис. 4. Графики функций j = f(L3, b, L1)
Анализ
графиков на рис. 4 показывает, что при l1 = const и равных интервалах варьирования l3 меньшим значениям аргумента l1 соответствуют большие интервалы значений
угла φ поворота карусели.
В
табл. 3 приведены значения угла φ,
полученные при постоянных значениях β
и l3
и варьировании l1.
Графики,
построенные по данным табл. 3, представлены на рис. 5. Анализ графиков на рис.
5 показывает, что при l3 = const и равных интервалах варьирования различных
значений аргумента l1 интервалы изменения угла j
уменьшаются по мере увеличения значений l1 и l3.
В
соответствии с целью статьи оценим точность срабатывания устройства, которая
будет определяться точностью воспроизводства углов β и φ в функции
параметров размерной цепи устройства с учетом первичных ошибок при определении
этих параметров.
Таблица 3. Углы φ
поворота карусели, град
|
l1, мм |
Длина l3, мм |
||
|
466 |
616 |
766 |
|
|
358 |
7.411 |
|
|
|
376 |
6.210 |
||
|
394 |
4.992 |
||
|
412 |
3.764 |
||
|
430 |
2.524 |
||
|
508 |
|
5.648 |
|
|
526 |
4.726 |
||
|
544 |
3.797 |
||
|
562 |
2.860 |
||
|
580 |
1.915 |
||
|
658 |
|
4.564 |
|
|
676 |
3.816 |
||
|
694 |
3.064 |
||
|
712 |
2.306 |
||
|
730 |
1.543 |
||
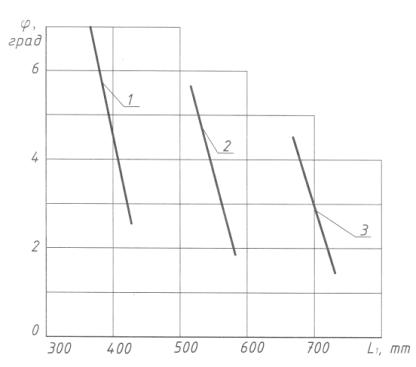
При значениях: b = 30, L3 = const, mm: 1 – 466, 2 – 616, 3 – 766
Рис. 5. Графики функций j = f (L1, b, L3)
Для
определения погрешности угла поворота заслонки напишем полный дифференциал
функции, представленной выражением (1)
 . (5)
. (5)
Заменим знаки дифференциала знаками первичных ошибок
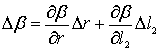 . (6)
. (6)
Определим частные производные при первичных ошибках Δr и Δl2.
Соответственно получим
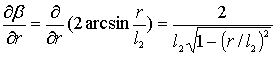 ; (7)
; (7)
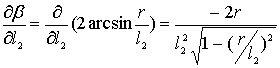 ,
(8)
,
(8)
где r и l2 − номинальное значение соответственно радиуса заслонки и длины O1B (см. рис. 2);
Δr и Δl2 - первичная ошибка в определении соответственно радиуса заслонки и
длины O1B.
Окончательно получим
 . (9)
. (9)
Здесь
Δβ − максимально
возможная ошибка в определении угла поворота заслонки при первичных ошибках
Δr и Δl2 в определении аргументов r и l2.
Равенство
(2) представим в виде суммы дифференциалов и выразим второе слагаемое второй
части
![]() ; (10)
; (10)
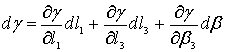 . (11)
. (11)
Представим частные
производные уравнения (11)
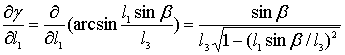 ;
(12)
;
(12)
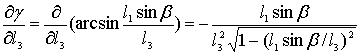 ;
(13)
;
(13)
 . (14)
. (14)
Заменяя
в уравнении (11) знаки дифференциалов знаками первичных ошибок, с учетом
частных производных, представленных выражениями (12), (13) и (14), получим
формулу для расчета максимально возможной ошибки в определении угла g
 . (15)
. (15)
Таким
образом, максимально возможная ошибка
Δφ в определении угла φ поворота карусели составит
![]() ,
(16)
,
(16)
где Δβ − ошибка в определении угла β, вычисленная
по формуле (9);
Δγ − ошибка в
определении угла γ, вычисленная
по формуле (15).
Выводы.
Получены
зависимости для расчета размерной цепи устройства по значениям его линейных и
угловых параметров.
Дан
анализ угловых параметров устройства в функции его линейных характеристик.
Проведен
анализ точности работы устройства и определены максимально возможные ошибки в
значениях угловых параметров.
Литература:
1.
Горлатов А. С.
Совершенствование набивочных машин в рыбоконсервном производстве / А.С.
Горлатов // Совершенствование процессов, машин и аппаратов рыбопереработывающих
произв.: Сб. науч. тр. КТИРПХ. – Калининград, 1992. – С. 28-46.
2.
А. с. 1785957
(СССР), МКИ В65В 25/06. Устройство для наполнения банок продуктом / А. С.
Горлатов, М. И. Носов, Е. Н. Сесюк. – 4847404. – Заявл. 09.06.90. – Опубл.
07.01.93. − Бюл. № 1.
3.
Патент №
2031817 (РФ), МКИ В65В 26/06. Устройство для наполнения банок продуктом / А. С.
Горлатов, Е.Н. Сесюк, И. В. Архипова. – 5004392. – Заявл. 17.09.91. – Опубл.
27.03.95. – Бюл. № 9.
4.
Патент №
2090471 (РФ), МКИ В65В 25/10, 3/00. Машина для наполнения банок продуктом / А.
С. Горлатов, И. В. Архипова, Е. Н. Сесюк. – 5015288. – Заявл. 02.12.91. –
Опубл. 20.09.97. – Бюл. № 26.
5.
Патент №
2131834 (РФ), МКИ В65В 25/10. Машина для наполнения банок продуктом / А. С.
Горлатов, А. А. Желнина. –98106493. – Заявл. 09.04.98. – Опубл. 20.06.99. – Бюл. № 17.