Мелащенко О.Н., Рыжков Л.М., Степуренко Д.И.

Национальный технический университет Украины «КПИ»

ИССЛЕДОВАНИЕ РЕЖИМА ПРЕДВАРИТЕЛЬНОГО УСПОКОЕНИЯ МИКРОСПУТНИКА ПОСЛЕ ЕГО ОТДЕЛЕНИЯ ОТ РАКЕТЫ-НОСИТЕЛЯ

После отделения от носителя микроспутник (МС) имеет большую угловую скорость вращения, которую перед его переводом в штатный режим работы необходимо уменьшить. На этом этапе функционирования МС использование датчиков Земли и Солнца невозможно. При отсутствии в системе управления МС гироскопических измерителей угловой скорости практически единственным способом получения информации об угловом движении МС является применение магнитометров.

В качестве исполнительных элементов системы управления будем рассматривать магнитные катушки. Гашение угловой скорости МС после его отделения от носителя происходит путем приложения к нему механического момента, который возникает в результате взаимодействия магнитного поля Земли (МПЗ) с магнитным полем катушек МС:

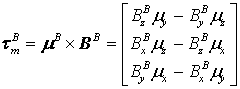(1)

где – суммарный магнитный момент, создаваемый катушками, – вектор индукция МПЗ.

Магнитный момент формируется следующим образом [1-3]:

(2)

где – коэффициент, – продифференцированный сигнал магнитометров, установленных на борту МС.

Идея применения закона (2) заключается в формировании управляющего момента, рассеивающего кинетическую энергию спутника. Это имеет место, если момент управления перпендикулярен локальному вектору индукции МПЗ.

Уравнения движения МС запишем в форме

(3)

где – тензор моментов инерции МС; – абсолютная угловая скорость МС, выраженная в связанной системе координат; – угловая скорость МС относительно орбитальной системы координат, выраженная в связанной системе координат; – кососимметрическая матрица; – момент, действующий на МС.

Запишем выражение для механического момента, который прикладывается к МС во время успокоения:

.

Поскольку , то выражение для производной вектора индукции МПЗ запишется в виде:

Возле Северного и Южного полюсов магнитное поле приблизительно постоянное. Поэтому последнее выражение может быть аппроксимировано как:

.

Это предположение справедливое только в полярных областях. Возле экватора скорость геомагнитного поля достигает своего максимального значения, которое может быть аппроксимировано как:

.

Энергия спутника определяется выражением:

,

где – кинетическая и – потенциальная энергии. При свернутой штанге величиной можно пренебречь и выражение для кинетической энергии запишется в виде:

.

Таким образом, функция Ляпунова запишется в виде:

.

Производная по времени от кинетической энергии равняется мощности, которая подводится магнитными катушками. Принимая постоянство величины геомагнитного поля в полярных областях, производная по времени от энергетической функции будет моментом. Итак, можно записать:

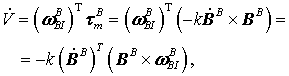
где использовано такое свойство векторного умножения .

Используя приближенное равенство для производной вектора индукции МПЗ можно записать следующее выражение для производной функции Ляпунова:

которая является отрицательно-полуопределенной. Итак, можно сделать вывод, что энергия системы рассеивается, и угловые скорости спутника уменьшаются.

Операция численного дифференцирования может быть реализована согласно разностного алгоритма:

, (4)

где – период дискретизации, – постоянная времени алгоритма дифференцирования.

Численное исследование режима успокоения МС выполнено в предположении, что МС движется по орбите с параметрами: . Тензор инерции спутника без штанги принят равным . При моделировании не учитывались возмущения, действующие на МС.

Предъявляемые требования заключаются в том, чтобы обеспечить значения угловых скоростей МС:

.

На рис.1 и рис.2 приведены графики изменения орбитальной угловой скорости МС при его успокоении. Для моделирования начальная угловая скорость МС выбрана в виде вектора . Коэффициент в законе (2) выбран равным соответственно 200000 и 1000000.

Как видно из рис.1 и рис.2, начальную угловую скорость МС удается погасить за время, примерно равное трем орбитальным виткам.

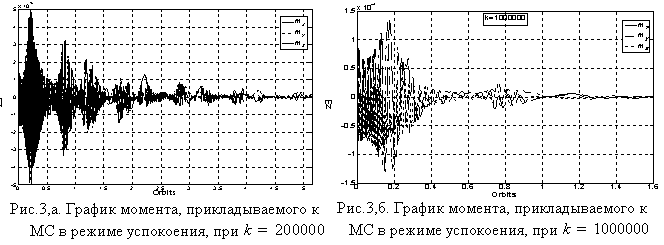На рис.3 приведены графики изменения момента, который прикладывается к МС. Как видно с рис.3,б, для успокоения МС за время одного орбитального витка к нему должен быть приложен момент порядка . Сравнивая рис.3,а и рис.3,б, можно сделать вывод, что за счет выбора коэффициента величину момента управления можно уменьшить на порядок. Это приведет к уменьшению габаритов магнитных катушек, однако при этом время успокоения увеличивается до пяти орбит.

Список литературы

1. Коваленко А.П. Магнитные системы управления космическими летательными аппаратами. – М.: Машиностроение, 1975. – 247 с.

2. Whiford C., Forrest D. The CATSAT Attitude Control System // Proceedings of the 12th Annual AIAA/USU Conference on Small Satellites, Logan, Utah, 1998.

3. Herron M., Goeree B., Shucler B. Detumbling of the UASat // Tecnical Note, Student Satellite Project, University of Arizona, 2000.