к.т.н. Поцепаев В.В.

Донецкий национальный университет, Украина

Алгоритмический метод моделирования нагрузок на роторных исполнительных органах машин

Расчет динамических нагрузок машин с роторными исполнительными органами, являющихся автономными системами, представляет весьма сложную вычислительную процедуру поскольку связан с пространственными перемещениями как исполнительного органа, так и самой машины. В докладе рассмотрен эффективный алгоритм моделирования нагруженности на примере угледобывающего комбайна.

Обзор современных методов исследования динамической нагруженности очистных комбайнов показывает, что вопрос определения фактической толщины стружки на резцах исполнительных органов является одним из ключевых, поскольку позволяет связать процессы формирования действующих нагрузок с динамикой машины.

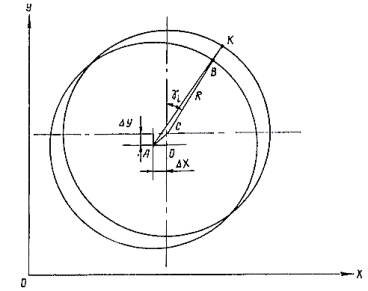
Рис. 1. К выводу формулы для определения толщины стружки

Определим толщину стружки i-го резца при его заданном угловом перемещении (рис. 1), предполагая, что i-я линия резания находится в фиксированной плоскости. Поскольку толщина стружки – это расстояние между режущими кромками резца в рассматриваемый момент времени (точка К) и в некоторый момент времени , когда резец пересекал луч СК, направленный от оси шнека к резцу (точка В), то обозначим радиус шнека СК через R, а горизонтальное (в направлении подачи) и вертикальное смещение (приращения координат) оси шнека через,. Отметим, что во введенной системе координат значения приращения неотрицательные, а значения приращения могут иметь любой знак. Дальнейшие рассуждения не зависят от знака , поэтому рассмотрим случай, приведенный на рис. 1 как общий.

Из треугольников ACD и ABC находим:

, ,

Используя теорему косинусов и функцию , окончательно получим

, (1)

где .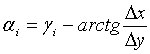

В формуле (1) значения приращений,, являются функциями пространственных координат исполнительного органа , , , определяемых из решения уравнений движения комбайна в пространстве лавы и уравнений динамики привода исполнительных органов:

, (2)

, (3)

, (4)

где , и , - соответственно абсцисса и ордината исполнительного органа в настоящий момент времени и в момент времени , когда впереди идущий резец, находящийся в одной линии резания с рассматриваемым i-тым резцом, пересекал радиус, имеющий угол наклона ; -угловая координата исполнительного органа в момент времени ; -начальный угол установки i-го резца на исполнительном органе.

Для одного резца в линии резания впереди идущим будет сам же рассматриваемый резец, и для нахождения приращений ,. необходимо знать его же координаты и на предыдущем обороте исполнительного органа. Следовательно, при алгоритмической и программной реализации формул (2) – (4) на каждом шаге вычисления (в очередном фиксированном положении исполнительного органа) в общем случае необходимо иметь предысторию , не менее чем за один оборот исполнительного органа.

В предлагаемом алгоритме формирование предыстории и вычисление выполняется через угол , определяемый как , где - число положений за один оборот исполнительного органа, в которых начисляются значения . Такой подход позволяет находить индекс строки с предысторией при любой вариации .

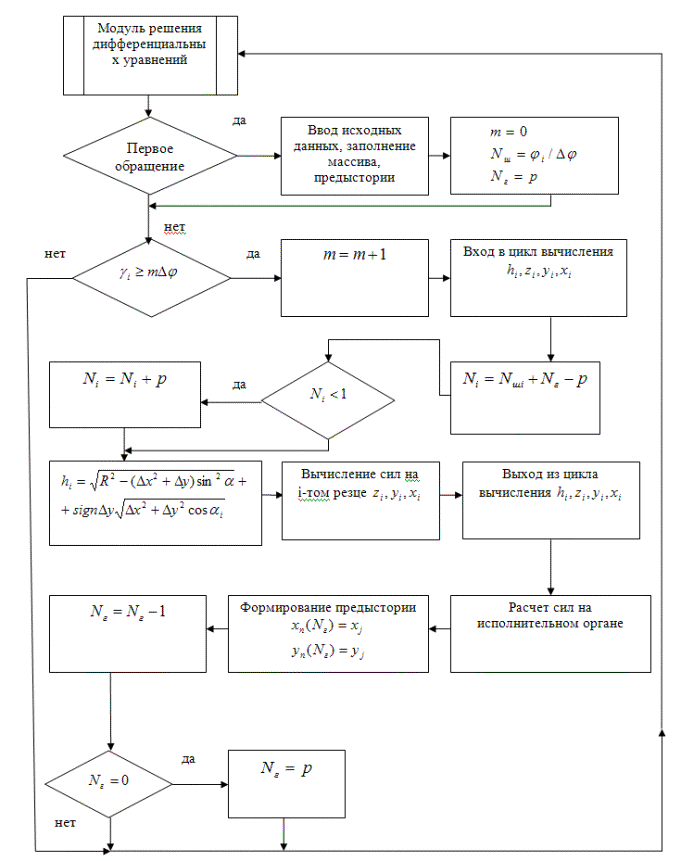
Рис. 2. Блок-схема универсального алгоритма расчета динамики комбайна

Выбор значения обусловлен сохранением частотных свойств и формы моделируемого спектра нагрузок на исполнительном органе.

Блок-схема универсального алгоритма расчета динамики комбайна представлена на рис. 2.

Первому вычислению по формуле (1) предшествует заполнение массива предыстории размерностью р х 2 координатами исполнительного органа за прошлый оборот, соответствующее равномерному перемещению и вращению исполнительного органа. Задается индекс номера границы последней строки массива с предысторией прошлого оборота равным р. Задается нулевое состояние счетчика шагов m. Вычисляется число шагов между i-тым резцом и впереди идущим. Для первого и каждого последующего шага вычисления определяется индекс строки с предысторией , вычисляются , по значениям которых находятся значения усилий на резцах и далее на исполнительном органе. Шаг заканчивается занесением текущих координат , в строку массива предыстории с индексом и вычислением для следующего шага.

Оценим погрешность вычисления , получаемую при применении рассматриваемого алгоритмического метода.

Формула (1) точная, но значения и определяются с погрешностью, обусловленной двумя факторами: во-первых, дискретные значения , последующего оборота шнека не соответствуют в общем случае угловому положению резца , во-вторых, алгоритмически поиск соответствующих углу значений , производится с ошибкой. Поэтому оценим устойчивость формулы (1) к погрешностям в определении положения оси шнека в предыдущей траектории резца. Качественный анализ показывает, что квадратный корень уменьшает ошибку, а монотонный рост от до при в промежутке не приводит к существенной ошибке в определении , следовательно, с учетом четности функций и формула (1) устойчива к погрешностям в определении , . Для количественной оценки погрешности определения нужно задать границы изменения, т.е. погрешности , . В связи с этим воспользуемся примером оценки максимальных значений ошибки определения положения оси исполнительного органа в предыдущем обороте шнека. Естественно, что с увеличением шага интегрирования дифференциальных уравнений динамики очистного комбайна ошибка в определении индекса , может увеличить погрешность в определении истинных значений указанных переменных. Поэтому выберем максимальный шаг интегрирования 0,01 с, тогда максимальная угловая ошибка составит 11,4, а ошибка в определении индекса , будет не больше 3. Примем скорость подачи 10см/с, а R=50см и отметим, что с ростом R погрешность в определении уменьшается.

Если истинное значение было 10 см, то, предположив пятикратное увеличение скорости оси шнека по сравнению со скоростью подачи в течение 0,03 с, получим ошибочное значение , равное 11,5 см. Ошибка в определении при истинном значении 10 см с учетом амплитуды и частоты вертикальных колебаний оси шнека не превышает 0,4 см.

Расчеты по формуле (1) при различных угловых положениях резца показывают, что погрешность в определении толщины стружки не превышает 4,9% при допущении погрешности только для 15%. Описанный пример оценки максимальной погрешности в определении полностью согласуется с качественным обоснованием устойчивости формулы (1), а численные значения ошибки в определении при практических расчетах на ЭВМ значительно меньше приведенного максимального значения.

Предлагаемый алгоритмический метод в сочетании с формулой (1) позволяет эффективно решать задачи исследования и оптимизации динамических систем горных машин, требующих моделирования рабочих и переходных режимов нагружения исполнительных органов.

Применение метода позволяет существенно расширить круг задач, решаемых методами имитационного моделирования.

Организация вычислительной фактической толщины стружки с шагом по углу поворота исполнительного органа позволяет непосредственно, осуществить стыковку разработанных программных модулей со стандартными программами решения дифференциальных уравнений.