Буревич А.А., Казнадий О.В.

Национальный технический университет Украины «КПИ»

Анализ влияния сухого трения в подвесах двигателей-маховиков на точность системы угловой стабилизации микроспутника

В данной работе рассматривается одноосная система угловой стабилизации микроспутника с двигателями-маховиками по принципу замкнутых систем автоматического регулирования. Сделан анализ влияния момента сухого трения в подшипниках двигателей-маховиков на точность системы управления.

Рассмотрим одноосную стабилизацию на примере канала тангажа. Также введем некоторые допущения:

-будим считать что нет возмущающих моментов по другим осям или предполагая что работа системы стабилизации по этим каналам идеальна и углы отклонения микроспутника очень малы;

- предположим, что есть датчики угла и угловой скорости микроспутника и что они имеют линейные характеристики.

В основу принципа действия таких систем, использующих в качестве исполнительных органов вращающиеся массы (маховики), положен закон сохранения момента количества движения. Вращающийся маховик как аккумулятор кинетической энергии компенсирует угловую скорость спутника и накапливает его кинетическую энергию, полученную от разных возмущающих факторов.

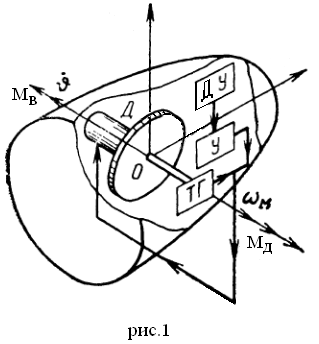
Допустим, что момент внешних сил (рис.1) стремиться отклонить микроспутник от первоначального положения. Угол отклонения измеряется датчиком угла ДУ и выдает электрический сигнал в усилитель. Далее преобразованный сигнал поступает в систему управления двигателями-маховиками, которая вырабатывает сигнал на изменение угловой скорости маховика таким образом, чтобы ликвидировать возникшее отклонение .

Пускай система угловой стабилизации будет с линейным законом управления, то есть момент двигателя-маховика будет формироваться пропорциональным углу отклонения микроспутника . Также введем в систему демпфирование. Прежде всего, в механической системе спутник-маховик имеются диссипативные моменты, обусловленные наличием вязкого трения в опорах и различными электромагнитными процессами, протекающими в двигателе. В первом приближении эти моменты пропорциональны угловой скорости . Известно, что естественного демпфирования в системах такого рода недостаточно для того, чтобы получить быстросходящийся переходной процесс. Поэтому введем в закон управления производную от угла , пологая, что она формируется при помощи датчика угловой скорости ДУС и какого нибудь исполнительного органа, к примеру магнитных катушек. Обозначим коэффициент суммарного демпфирования .

В соответствии с рис.1 и сделанными ранее допущениями уравнение движения микроспутника примет вид:

(1)

Где в уравнении (1) -момент инерции спутника по оси управления,

-момент создаваемый двигателем-маховиком.

Уравнение движения маховика:

(2)

Где -момент инерции маховика и вращающихся частей привода,

-абсолютный угол поворота маховика в инерциальном пространстве.

Как было ранее оговорено, момент управления будет формироваться пропорциональным , тогда . В идеале момент двигателя-маховика должен равняться моменту управления, но так как есть наличие сухого трения в опорах тогда:

(3)

Где - момент сухого трения в подшипниках двигателя-маховика.

Тогда уравнение движения маховика примет вид:

(4)

Подставив (3) в (1) получим:

(5)

Уравнение (5) является математической моделью, которая описывает поведение системы при действии возмущающих моментов и момента сухого трения.

Для оценки влияния трения на точность нужно найти решение уравнение (5).

Пускай внешний возмущающий момент изменяется по гармоническому закону:

,

где ,-амплитуда и круговая частота изменения внешнего возмущающего момента.

А сухое трение имеет характеристику, показанную на рис.2, которая описывается следующей закономерностью , где - угловая скорость вращения маховика относительно корпуса микроспутника.

Трение создает зону нечувствительности при . Когда на маховик поступает сигнал на формирования момента управления, который меньше момента трения, двигатель не может провернуть маховик. Величина этой зоны определяется исходя из неравенства:

(6)

Условие (6) показывает максимально возможную точность стабилизации, то есть минимальные значения углов отклонения спутника, на которые система угловой стабилизации СУС будет реагировать. При проектировании такой системы должно как минимум выполняться условие (7), где -максимальное значение угла отклонения микроспутника, которое должна обеспечивать СУС.

Итак, первое негативное влияние трения проявляется уже вначале процесса стабилизации (), создавая мертвую зону, что снижает точность стабилизации микроспутника.

Теперь рассмотрим случай когда . Так как момент сухого трения имеет нелинейную характеристику найдем решение (7) на участке когда

.

(7)

Решение будет описывать характер движения спутника по каналу тангажа в установившемся режиме, предполагая, что свободные колебания были успокоены:

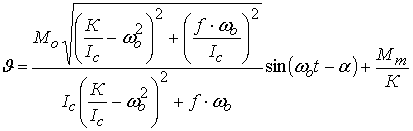(8)

где .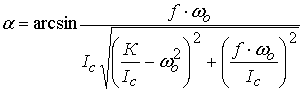

Из выражения (8) видно, что спутник будет совершать колебательное движение относительно смещенного положения, представляющего собой дополнительную статическую ошибку (9). Первое слагаемое в (8) при синусе характеризует ошибку СУС от недокомпенсации возмущающего момента.

Трение можно рассматривать как потери части сигнала которое идет на формирование момента управления. Когда из ДУ приходит сигнал в двигатель-маховик, его система управления создает момент. Часть управляющего момента тратиться на преодоление трения. Из-за этих потерь возникает дополнительная погрешность СУС, которая постоянная и обратно пропорциональна . Следовательно эту погрешность можно уменьшить путем увеличения в системе.

Количественную оценку погрешности от трения характеризует выражение (9).

Найдем качественную оценку этой погрешности, которая сможет дать нам ответ на вопрос: нужно ли обращать внимание при проектировании СУС на трение в опорах двигателя? Ведь возможен вариант что статическая погрешность от трения намного меньше от ошибки недорегулирования. То есть если выполняется условие (10), то трением можно пренебречь.

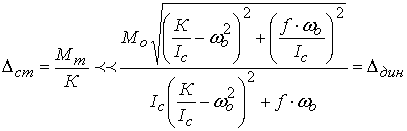(10)

- динамическая погрешность, которая численно равна максимальному углу отклонения микроспутника при отсутствии трения в опорах и действием гармонического возмущающего момента с частотой и амлитудой .

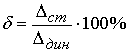(11)

Если , то тогда трением можно пренебречь и полностью и сосредоточится на обеспечении в заданных диапазонах.

Так как примерно численно равна орбитальной угловой скорости вращения спутника вокруг Земли, является сравнительно малой величиной(0.0011рад/сек), то составляющими при можно пренебречь, тогда:

(12)

Из выражения (12) видно что дополнительный вклад погрешности от трения относительно динамической погрешности зависит только от соотношения момента трения и возмущающего момента и не зависит от параметров системы. Это подтверждает то что дополнительная погрешность вызванная трением возникает от потерь части управляющего момента из-за момента трения, которое препятствует вращению маховика.

Выражение (12) еще на начале проектирования СУС дает ответ на вопрос, нужно ли учитывать трение в опорах двигателя-маховика. Если величина момента трения на порядок меньше чем внешний возмущающий момент, то тогда трением можно пренебречь.

Допустим маховик попал в мертвую зону и остановился. Момент создаваемый двигателем-маховиком будет равен нулю. Далее спутник будет продолжать вращаться под действием только возмущающего момента .

Но как только маховик вновь начнет вращаться относительно корпуса спутника. Возникший момент от двигателя вызовет собственные колебания спутника. Так как в нашей системе присутствует демпфирующее устройство то собственные колебания через определенное время затухнут.

Негатив такого влияния проявляется, если спутник сильно отклоняется и если время переходного процесса велико.

Поскольку уравнение (7) линейное на временных участках, когда одного знака, то можно применить теорему о суперпозиции.

Общее решение будет сумой решений уравнений:

;

;

(13)

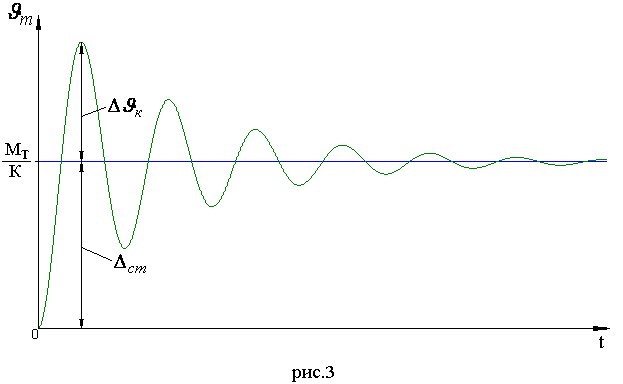
- угол отклонения спутника от действия возмущающего момента

- угол отклонения спутника от действия момента сухого трения (рис.3)

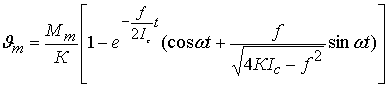(14)

где .

Моделирование такой системы угловой стабилизации показана на рис.4

,

Начальный угол и угловая скорость спутника по тангажу равны нулю, начальная угловая скорость маховика -230 рад/сек.

На рис.4 видно что при прохождении маховика через мертвую зону возникают собственные колебания спутника.

На рис.5 показаны два графика угла отклонения спутника:

- при наличии момента сухого трения

- когда сухое трение отсутствует

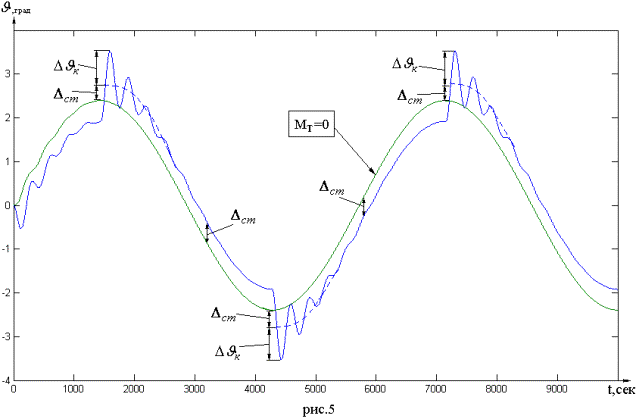
Таким образом, наличие сухого трения в подшипниках двигателя маховика ухудшает точность системы угловой стабилизации, а именно:

-Создает зону нечувствительности;

-Вносит дополнительную статическую погрешность ;

-Вызывает собственные колебания системы;

Литература

1. Каргу Л.И. Системы угловой стабилизации космических аппаратов -М.: Машиностроение, 1980.-172с., ил.

2. Павловський М.А. Теоретична механика: Підручник.-К.: Техніка, 2002.-512с.: іл..