УДК 539.3

А.К.Кудайкулов, Б.Р.Арапов, Б.З.Кенжегулов, К.Б.Амиртаев, У.Б.Утебаев, Б.М.Токкулиев

Республика Казахстан, г.Туркестан, МКТУ им.Х.А.Ясави

ЧИСЛЕННОЕ РЕШЕНИЕ ЗАДАЧИ УСТАНОВИВЩИЕСЯ ТЕРМОНАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ТЕПЛООБМЕННИКА, ПРИ НАЛИЧИИ ВНУТРЕННЕГО ТЕПЛОВОГО ПОТОКА И НАРУЖНОГО ТЕПЛООБМЕНА ПОСТОЯННОЙ ИНТЕНСИВНОСТИ

Теплообменниками являются совокупность труб ограниченной длины L [см], постоянного поперечного сечения F [см²], обе концы которого жестко защемлены на массивные диски. Коэффициент теплопроводности материала трубы , коэффициент теплового расширения , а модуль упругости . Коэффициент теплообмена между наружной поверхности трубы и окружающей ее средой . Температура окружающей среды . Внутренний радиус трубы а наружная . Площадь поперечного сечения трубы . Предположим, что через внутри трубы проходит установившиеся тепловой поток постоянной интенсивности, т.е. значение зависит от координаты х. В то время через точки наружной поверхности трубы происходит установившиеся теплообмен постоянной интенсивности окружающей ее средой. Площади поперечных сечений защемленных обеих концов считаем теплоизолированными. Условная схема рассматриваемой задачи в разрезе трубы показано на рис-1.

а)

б)

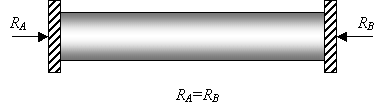
Рис-1. а) Условная схема в разрезе; б) Условная схема жестко защемленной двумя концами трубы.

Рассматриваемую трубу делим на n-квадратичных конечных элементов одинаковой длины с тремя узлами. В пределах каждого конечного элемента распределение поле температур T(x) аппроксимируем гладкой кривой второго порядка [1,2], т.е.

, (1)

где функции формы для каждого квадратичного конечного элемента с тремя узлами [1,2].

(2)

где - длина каждого конечного элемента.

Здесь локальные переменные. Например для m-го конечного элемента Для этого m-го элемента напишем выражение функционала характеризующую полную тепловую энергию 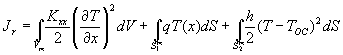[3].

, (3)

где V_m- объем m-го конечного элемента; - площадь внутренней поверхности m-ой части трубы. Куда подведен тепловой поток постоянной интенсивности q=const; - площадь наружной поверхности m-ой части трубы, через которого происходит теплообмен с окружающей этой поверхности средой.

Интегрированный вид первого интеграла в выражении (3) будет следующим

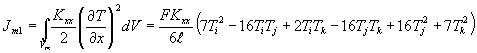. (4)

Аналогично для второго члена (3) имеем

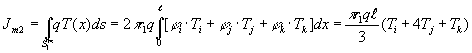. (5)

Для третьего члена (3) имеем

. (6)

Тогда для m-го элемента интегрированный вид функционала (3) в целом имеет следующий вид

. (7)

Аналогично для всей рассматриваемой трубы имеем

, (8)

где n-общее количество конечных элементов в трубе.

Далее минимизируя J по , получим следующую систему линейных алгебраических уравнений

, (9)

где .

Решая эту систему определяются узловые значения , затем по (1) строится поле распределения температур по всей длине рассматриваемой трубы. После чего согласно [3,4] определяется величина удлинения трубы от поле распределения температур (в случае не защемленной трубы)

. (10)

Так как обе концы трубы жестко защемлены, то вследствие теплового воздействия в обеих защемленных концах возникает сжимающее усилие R. Значение укорачивания за счет этого сжимающего усилия, согласно закону Гука [4,5] будет равно

. (11)

Исходя из постановки рассматриваемой статически неопределимой задачи имеет место, что

. (12)

Тогда с учетом (10, 11) из (2) имеем

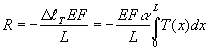. (13)

В таком случае значение термоупругого напряжения определяется в соответствии законом Гука следующим образом

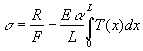. (14)

Теперь решим рассматриваемую задачу при следующих исходных данных:

При этих исходных данных имеем, что , где Тогда значение сжимающего усилия будет следующим

Значение термоупругого напряжения будет и оно постоянно по всей длине рассматриваемой трубы. Как видно из рассматриваемой задачи из за теплового расширения в некоторых теплообменниках значение термоупругого напряжения сжатия могут превосходит его предела прочности. Это явление еще раз показывает актуальности исследования термоупругости теплообменников при разных вариациях как внутренних тепловых полей, так и температуры окружающей ее наружной поверхности.

Список использованных литератур.

1. Зенкевич О., Метод конечных элементов в технике, изд-во «Мир», М., 1975.

2. Сегерлинд Л. Применение метода конечных элементов. М.: Мир, 1979, 392-стр.

3. Ноздрев В.Ф. Курс термодинамики. М.: Просвещение, 1967.

4. Тимошенко С.П., Гудьер Дж ., Теория упругости, изд-во «Наука», М., 1975.

5. Писаренко Г.С. и др., Сопротивление материалов, “Вища Школа”, Киев, 1973, 672 с.