Технические науки

МЕХАНИКА

УДК 624.078.54:621.891

Бондаренко Л.Н., Яковлев С.А., Бычков В.В., Масалкин Я.А.

Днепропетровский национальный университет железнодорожного транспорта им. акад. В. Лазаряна

Дополнение к „парадоксу трения” с учётом сопротивления качению

Без учёта трения каченя колеса проявлене особенности „парадокса трения” рассматривается на примере тормозного устройства, показанного на рис. 1.

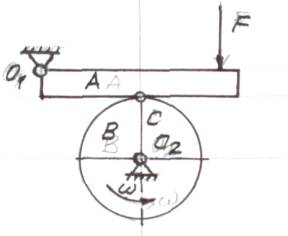
Рис. 1. Схема к рассмотрению „парадокса трения”

без сопротивления качению

Суть особенности заключается в следующем. Тормозная колодка мо-

жет вращаться вокруг неподвижной оси. Колесо вращается вокруг оси . В точке оба тела касаются друг друга. Коэффициент трения скольжения между этими телами равен .

Пусть к колодке приложена сила , которая прижимает колодку к коле

су. Если составить уравнение движения колеса, обозначив через его массу, через момент инерции, а через - угловую скорость вращения, то из уравнения равновесия колеса и колодки без учёта сопротивления качению можно получить, что

(1)

и при <вывести колесо из состояния покоя и заставить его вращаться против часовой стрелки нельзя. Если прикладывать к колесу силы со сколь угодно большим моментом () это приведёт лишь к одновременному увеличению силы трения.

С другой стороны, при <0 уравнение движения не имеет решения.

Без учёта сопротивления качению колеса выходит, что угловая скорость уменьшается и при

(2)

происходит остановка колёса.

Получим формулы (1) и (2) с учётом сопротивления качению колеса (рис. 2).

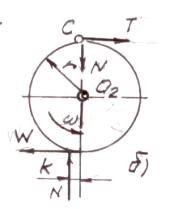
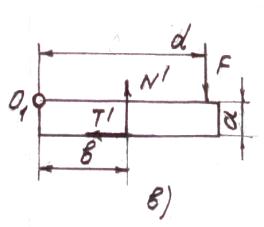
Рис. 2. Схемы к рассмотрению „парадокса трения” с учётом

сопротивления качению

Запишем уравнение движения колеса, пренебрегая силой F по сравнению с Р при массе колеса m

, (3)

где - коэффициент трения качения. Если ширина рельса , модули упругости материалов колеса и рельса одинаковы, а коэффициенты Пуассона равны 0,3 , то при схеме касания цилиндр – плоскость полуширина полоски контакта [1]

,

а радиус колеса из условия равенства контактных напряжений допускаемым

и предыдущая формула принимает вид

.

Нами доказано, что при первоначальном линейном контакте коэффициент трения качения [2]

(4)

Подставив выражение для k из (4) в (3), получим

. (5)

Уравнение равновесия рычага А

. (6)

Одним из решений этого уравнения будет

если > 0 , то (7)

и, следовательно, при выполнении условия

> (8)

можно найти, затем найти и решить уравнение (5).

Если уравнение (8) нарушить, например за счёт увеличения или подобрать пару с большим коэффициентом трения, то уравнение (6) не имеет решения и. следовательно, нельзя определить правую часть уравнения (5).

Парадокс состоит в том, что рычаг А как будто обязан находиться в равновесии, поскольку сумма сил Т^′ и N′ имеет относительно оси О₁ момент того же знака. Что и момент силы F (рис. 2г). Т.е. рычаг должен начать вращаться по часовой стрелке под действием приложенных к нему сил. Но такое движение не может начаться в отличие от случая, когда колесо вращается в другом направлении и задача имеет полное решение.

Из (7) величина силы трения

и после подстановки в (5), получим

. (9)

Это уравнение замедляющего вращения. Его решение

, (10)

где - начальная угловая скорость, с которой колесо вращалось до того , как колодка была прижата к нему во время .

Из (10) следует, что угловая скорость колеса уменьшается и

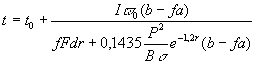. (11)

Если без учёта сопротивления качению время до остановки прямо пропорционально величине (остановка происходит тем скорее, чем меньше ), то с учётом сопротивления ответ на этот вопрос не однозначен: всё зависит от величины сопротивления качению, которая умножается на эту же разницу. Однако, при время торможения равно нулю и в этом случае.

Для определения максимальной величины силы трения скольжения будем считать, что (колесо покоится), и попытаемся сдвинуть его по стрелке. Из уравнения равновесия колеса и колодки

;

можно получить

;

.

Составим разницу

<0 (12)

при < вывести колесо из состояния покоя и заставить его вращаться против часовой стрелки невозможно.

Литература:

1. Справочник по сопротивлению материалов/ Писаренко Г.С., Яковлев А.П.,

Матвеев В.В. – Киев: Наук. думка, 1988. – 736 с.

2. Бондаренко Л.М., Довбня М.П., Ловейкін В.С. Деформаційні опори в машинах. Дніпропетровськ: Дніпро – VAL, 2002. – 200 с.