Отраслевое машиностроение-3

Аспирант Корчак Н.Н.

К. ф.-м. н. Андреев А.А

Подольский государственный аграрно-технический университет, Украина

Анализ динамических свойств малонагруженных фрезерных устройств в условиях периодической внешней нагрузки

Одной из главных проблем современного сельского хозяйства является создание устройств, которые бы выполняли определённые технологические операции с возможно минимальным потреблением энергии. Существующие рабочие органы сравнительно массивные. Это приводит к целому ряду нежелательных для них свойств. Во – первых, резко возрастает абразивный износ поверхностей, работающих в почве. Во – вторых, возрастают тяговые усилия и давления на почву. И, наконец, значительная инерционность таких элементов лишает возможности устройства к быстрой маневренности. Особенно наглядно эти “негативы” проявляются при увеличении скорости движения почвообрабатывающих устройств. Рассматриваемый в предлагаемой работе элемент предназначен для измельчения растительных остатков толстостебельных культур в полевых условиях после основной уборки урожая. Находящиеся впереди режущего элемента устройства формируют растительные остатки в направлении, удобном для измельчения.

Предлагаемое устройство (рис. 1) представляет собой два металлических диска 1, жёстко скреплённых между собой, которые вращаются на валу 3. Перпендикулярно к их плоскости (при работе она вертикальная) прикреплено количество n ножей 2. Диски вращаются с угловой скоростью:

ω > V₀R^-1 (1)

где V₀ – скорость движения агрегата;

R – радиус диска.

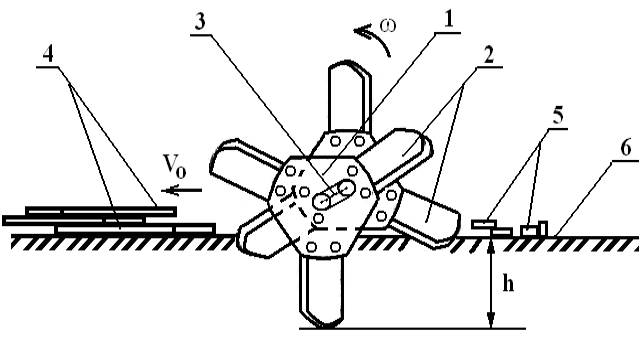
Рис. 1. Схематическое изображение фрезерного устройства для

измельчения растительных остатков:

1 – диск; 2 – ножи; 3 – вал; 4, 5 – растительные остатки; 6 - почва

Неравенство предполагает наличие независимого привода на вал устройства. При вращении ножи режут растительные остатки 4, оставляя измельчённые остатки 5. Безусловно, рассматриваемое устройство имеет аналоги, но эти аналоги работают в стационарных условиях, и условия измельчения значительно отличаются от работы в полевых условиях (небольшая плотность остатков 3, специфические свойства почвы 6 и т.п.). Понятно, что в этих условиях неизбежным является углубление ножей 2 в почву на глубину (h – усредненное, зависящее от рельефа почвы значение).

Запишем динамическое уравнение движения устройства:

(2)

где I – момент инерции устройства;

М – крутящий момент;

М − момент сил трения;

М₁( t ) – момент сил лобового сопротивления почвы.

Для сравнительно небольших угловых скоростей без взаимодействия с почвой можно принять . Решение уравнения (2) без третьего слагаемого в правой стороне носит асимптотический характер, причём с достаточной точностью переходной процесс можно считать оконченным с выходом на ω₀ при t > 3τ ( τ = IM₀^-1, ω – установившаяся частота).

Преобразуем уравнение (2) к следующему виду:

; ; ; (3)

Стандартное интегрирование уравнения (3) даёт:

(4)

Здесь С – константа интегрирования. Её значение несущественно, так как при последнее слагаемое в (4) стремится к нулю. Интеграл в (3) определяется видом M₁( t ). Вполне очевидно, что М₁( t ) является импульсной функцией (рис. 2) времени. Так, на позиции а) точки n (t₁+∆t) – начало вхождения ножа в почву, nt₁+(n-1)∆t – момент выхода. Импульсный характер М₁( t ) позволит записать:

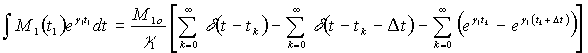(5)

Здесь δ (t – t_k) – дельта – функция Дирака.

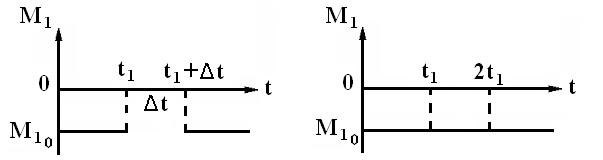
а) б)

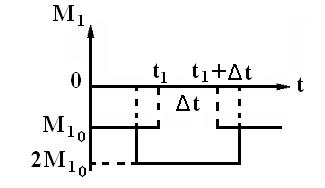
в)

Рис. 2. Качественная зависимость момента М₁ от времени t

Легко можно увидеть, что минимальным внешним влиянием будет такой вид импульсов, когда ∆t = 0 (случай б). В этой ситуации выражение (5) равно нулю, и выражение (4) позволяет определить константу интегрирования С:

(6)

Откуда

(7)

Вышеприведённые расчёты позволяют произвести определённую оптимизацию предлагаемого устройства. Основными предположениями для оптимизации могут быть следующие:

- оптимальная для резания растительных остатков глубина ;

- обеспечение условия ∆t=0 подбором числа режущих элементов 2, то есть, выбор и n таким образом, чтобы выполнялся режим работы б (рис. 2);

- подбор угловой скорости ω₀ и поступательной скорости агрегата V₀ таким образом, чтобы, во – первых, измельчённые остатки были минимально возможными, а во – вторых, не образовывалась бы пылевая фракция.

Литература:

1. Лурье И.А. Крутильные колебания в дизельных установках. – М., Наука, 1940;

2. Ден – Гартог Дж. Теория колебаний. – М., Гостехиздат, 1942;

3. Карман Т., Био М. Математические методы в инженерном деле. – М. – Л., ГТТИ, 1946.