Чиркова
Л.Н., к.п.н.
Вятский
Государственный Университет, Россия
Некоторые
свойства верхнего и нижнего пределов функций
Напомним понятие верхнего предела
функции f(x). Пусть точка x0 – предельная точка области
определения ![]() функции f(x).
Число а – верхний
предел функции f(x) при
функции f(x).
Число а – верхний
предел функции f(x) при ![]() (обозначается символом
(обозначается символом
![]() ), если выполняются следующие условия:
), если выполняются следующие условия:
1) ![]()
![]() :
: ![]() и
и ![]()
![]()
![]() ;
;
2) ![]()
![]() ,
, ![]() ,
, ![]() :
: ![]() .
.
Если в любой проколотой окрестности точки x0 функция принимает как
угодно большие положительные (отрицательные) значения, то по определению
полагаем: ![]() (
(![]() ). Аналогично вводится понятие нижнего предела функции.
). Аналогично вводится понятие нижнего предела функции.
Согласно [1, с. 38-40],
воспроизведем некоторые свойства верхнего и нижнего пределов функций. Считаем,
что x0 является предельной
точкой пересечения областей определения рассматриваемых функций f(х) и g(х).
Кроме того, исключаем
случаи, когда верхние и нижние пределы образуют какие-либо неопределенности (![]() ,
, ![]() ,
, ![]() ,
, ![]() ), поскольку для «раскрытия неопределенности» недостаточно
знать лишь верхние (нижние) пределы функций f(х) и g(х), а нужно учесть и самый закон их
изменения. Для примера рассмотрим частное
), поскольку для «раскрытия неопределенности» недостаточно
знать лишь верхние (нижние) пределы функций f(х) и g(х), а нужно учесть и самый закон их
изменения. Для примера рассмотрим частное ![]() и пусть обе функции –
верхние бесконечно малые при
и пусть обе функции –
верхние бесконечно малые при ![]() (о верхнем пределе их
отношения, не зная самих этих вариант, никакого общего утверждения сделать
нельзя). Пусть
(о верхнем пределе их
отношения, не зная самих этих вариант, никакого общего утверждения сделать
нельзя). Пусть 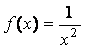 и
и ![]() . Обе функции являются верхними бесконечно малыми при
. Обе функции являются верхними бесконечно малыми при ![]() :
: ![]() и
и ![]() . Их отношение
. Их отношение 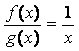 также является верхней
бесконечно малой при
также является верхней
бесконечно малой при ![]() . Если же, наоборот,
. Если же, наоборот, ![]() и
и 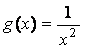 (по-прежнему обе
функции – верхние бесконечно малые при
(по-прежнему обе
функции – верхние бесконечно малые при ![]() ), верхний предел их отношения равен:
), верхний предел их отношения равен: 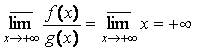 . Наконец, если
. Наконец, если ![]() и
и ![]() (обе функции – верхние
бесконечно малые при
(обе функции – верхние
бесконечно малые при ![]() ), верхний предел их отношения равен:
), верхний предел их отношения равен: 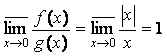 . Таким образом, верхний предел данного неопределенного
выражения, в зависимости от частного закона изменения обеих переменных, может
иметь различные значения.
. Таким образом, верхний предел данного неопределенного
выражения, в зависимости от частного закона изменения обеих переменных, может
иметь различные значения.
Свойства
верхнего и нижнего пределов функций
1) Пусть
функция f(х) определена в некоторой окрестности ![]() точки x0 и в данной точке имеет
предел, равный а (
точки x0 и в данной точке имеет
предел, равный а (![]() ,
,![]() ). Тогда это условие равносильно равенству а верхнего и нижнего пределов функции f(х) в точке x0:
). Тогда это условие равносильно равенству а верхнего и нижнего пределов функции f(х) в точке x0:
![]()
![]()
![]() .
.
2) Пусть
функции f(х) и g(х) определены в некоторой окрестности ![]() точки x0. Справедливо утверждение:
верхний предел в точке x0
суммы функций f и g
не превосходит суммы верхних пределов данных функций в этой в точке, т.е.
точки x0. Справедливо утверждение:
верхний предел в точке x0
суммы функций f и g
не превосходит суммы верхних пределов данных функций в этой в точке, т.е.
![]() .
.
Если же одна из
рассматриваемых функций в точке x0
имеет обычный предел, то соотношение данное выполняется со знаком равенства:
![]() .
.
Аналогично
формулируется свойство и для нижнего предела суммы функций в данной точке:
нижний предел в точке x0
суммы функций f и g
не меньше суммы нижних пределов данных функций в этой точке:
![]() .
.
Последнее соотношение
выполняется со знаком равенства, если одна из функций в точке x0 имеет обычный предел: ![]() .
.
3)
Пусть функция f(х) определена в некоторой окрестности ![]() точки x0. Тогда верхний предел в
данной точке функции −f(х) равен нижнему пределу в точке x0 функции f(х), взятому со знаком «минус»:
точки x0. Тогда верхний предел в
данной точке функции −f(х) равен нижнему пределу в точке x0 функции f(х), взятому со знаком «минус»:
![]() .
.
4) Пусть
функции f(х) и g(х) определены в некоторой окрестности ![]() точки x0. Верно утверждение: верхний
предел в точке x0 разности
функций f(х) и g(х) не превосходит разности верхнего и нижнего пределов
соответственно функций f(х) и g(х) в точке x0:
точки x0. Верно утверждение: верхний
предел в точке x0 разности
функций f(х) и g(х) не превосходит разности верхнего и нижнего пределов
соответственно функций f(х) и g(х) в точке x0:
![]() .
.
Если же одна из функций
в точке x0 имеет обычный
предел, то последнее соотношение выполняется со знаком равенства:
![]() .
.
5) Пусть
функции f(х) и g(х) определены и неотрицательны в некоторой окрестности ![]() точки x0. Верхний предел в точке x0 произведения функций не
превосходит произведения верхних пределов функций f(х) и g(х) в точке x0:
точки x0. Верхний предел в точке x0 произведения функций не
превосходит произведения верхних пределов функций f(х) и g(х) в точке x0:
![]() .
.
Если же одна из функций
в точке x0 имеет обычный
предел, то указанное соотношение выполняется со знаком равенства. Кроме того,
аналогично формулируется свойство и для нижнего предела произведения функций в
данной точке: нижний предел в точке x0
произведения функций не меньше произведения нижних пределов функций f(х) и g(х) в точке x0 (со знаком равенства, если одна из функций в точке x0 имеет обычный предел):
![]() .
.
6) Пусть
функция f(х) определена и сохраняет постоянный знак в некоторой проколотой
окрестности ![]() точки x0. Справедливо утверждение:
верхний предел в данной точке функции
точки x0. Справедливо утверждение:
верхний предел в данной точке функции ![]() равен единице,
деленной на нижний предел в точке x0
функции f(х):
равен единице,
деленной на нижний предел в точке x0
функции f(х):
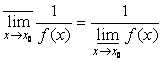 .
.
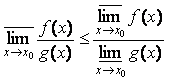
7) Пусть
функции f(х) и g(х) определены и неотрицательны в некоторой окрестности ![]() точки x0. Верхний предел в точке x0 частного функций f(х) и g(х) не превосходит частного верхнего и
нижнего пределов соответственно функций f(х) и g(х) в точке x0:
точки x0. Верхний предел в точке x0 частного функций f(х) и g(х) не превосходит частного верхнего и
нижнего пределов соответственно функций f(х) и g(х) в точке x0:
 .
.
Если же одна из функций
в точке x0 имеет обычный
предел, то указанное соотношение выполняется со знаком равенства.
8)
Пусть функция f(х) определена в некоторой окрестности ![]() точки x0. Нижний предел данной
функции в точке x0 не
превосходит ее верхнего предела в указанной точке:
точки x0. Нижний предел данной
функции в точке x0 не
превосходит ее верхнего предела в указанной точке: ![]() .
.
Литература:
1.
Брайчев Г. Г. Введение в теорию роста
выпуклых и целых функций. М.: Прометей, 2005. 232 с.
2.
Чиркова
Л. Н. Понятие верхнего и нижнего пределов функций // Materiály XII mezinárodní vědecko-praktická conference «Vědecky průmysl evropského kontinentu − 2016»/ − Díl 11. Zemědělství. Geografie a
geologie. Matematika: Praha. Publishing House «Education and Science» s.r.o. C.82-84.