УДК 534.121.2
Н.Ш.
Жолдасбекова, В.К. Бишимбаев, Б.С. Шакиров
Южно-Казахстанский государственный университет им. М.Ауезова
Моделирование переноса в мембранах с учетом скин-слоя при очистке
подземных вод
Асимметрия, т.е. различие коэффициентов переноса по обе стороны мембраны или при
изменении направления потока, сильно влияет на функциональные характеристики и
возможности использования мембран. Основная трудность при использовании
классических мембран, работа которых основана на эффекте ультрафильтрации,
состоит в том, что при повышении плотности пленки с целью увеличения ее
сепарационных характеристик, уменьшается ее проницаемость для воды и
существенно возрастает гидродинамическое сопротивление. Снижение толщины пленки с целью уменьшения
сопротивления также не способствует возрастанию селективности и, с другой
стороны, приводит к снижению прочности мембран.
Разделяющее действие асимметричных мембран основано на
эффекте обратного осмоса [1, 2, 3].
Обычно, для получения обратноосмотического эффекта используются
идеальные полупроницаемые мембраны, которые пропускают только воду, задерживая
низкомолекулярные электролиты. Сопротивление асимметричных обратноосмотических
мембран Лоэба-Сурираджана [1, 2] может быть достаточно малым, т.к. по своей
структуре в глубине эти мембраны являются микропористыми. Эффект асимметрии
достигается тем, что описываемые мембраны содержат очень тонкие участки с
плотным поверхностным слоем. Такая структура позволяет при высоких прочностных характеристиках мембраны в
целом, добиваться высокой селективности разделения веществ.
Технология создания тонкого поверхностного слоя
(скин-слоя) в современных полимерных обратноосмотических мембранах разнообразна [3, 4]. Обычно скин-слой
наносят из различных материалов, создавая композиционные мембраны. Одним из
наиболее перспективных технологических способов изготовления композиционных
мембран является межфазная полимеризация.
Несмотря на все более широкое распространение
микропористых обратноосмотических мембран, особенно при промышленном
обессоливании воды, механизмы процессов переноса в таких мембранах описаны пока
слабо.
В настоящей работе осуществлен физико-химический
анализ механизмов массопереноса в асимметричных микропористых мембранах и
предлагается подход к математическому моделированию этих процессов. Основное
внимание уделено выявлению условий, при которых воздействия на
симметричную мембрану приводят к возникновению асимметричной мембранной
системы, например за счет адсорбции ионов на поверхности.
Рассмотрим систему, в которой установилось межфазовое
равновесие между двумя электролитами и поверхностями мембраны, т.е. выполняется
условие равенства поверхностных и внутренних электрохимических потенциалов
каждого компонента:
![]()
![]() , (1)
, (1)
![]() . (2)
. (2)
Очевидно, что асимметричность мембраны может
возникнуть и при отсутствии скин-слоя. Симметричная мембрана с одинаковыми
параметрами адсорбции ионов на ее
поверхностях приобретает асимметричность,
помещенная между различными жидкостями. Действительно, равновесные
концентрации ионов в различных электролитах
различны, и поверхностные заряды мембраны будут меняться неодинаковым образом.
При низкой концентрации ионов в жидкости будет
происходить десорбция, и за счет этого мембранный потенциал будет приближаться
к значению, характерному для незаряженной мембраны. В то же время, при
достаточно больших концентрациях электролитов мембранный потенциал определяется
в первую очередь диффузионным потенциалом и почти не зависит от заряда мембраны [4]. Поэтому он не меняется в процессе десорбции.
В асимметричных мембранах возникает другая ситуация.
Коэффициентs распределения ионов ![]() -ro вида на обеих поверхностях можно описать следующими уравнениями [2,4],
содержащими два экспоненциальных члена, в показатели которых входят разности
стандартных химических потенциалов и потенциалов поверхности соответственно:
-ro вида на обеих поверхностях можно описать следующими уравнениями [2,4],
содержащими два экспоненциальных члена, в показатели которых входят разности
стандартных химических потенциалов и потенциалов поверхности соответственно:
 ,
(3)
,
(3)
 , (4)
, (4)
где ![]() ,
, ![]() - химические
активности компонентов
- химические
активности компонентов ![]() в потоке с обеих сторон;
в потоке с обеих сторон;
![]() ,
, ![]() - химические
активности компонентов в окрестности
поверхности мембраны с обеих сторон;
- химические
активности компонентов в окрестности
поверхности мембраны с обеих сторон; ![]() - разности
стандартных химических потенциалов в
ядре потока и на поверхности мембраны с обеих сторон;
- разности
стандартных химических потенциалов в
ядре потока и на поверхности мембраны с обеих сторон; ![]() - разности
электрических потенциалов поверхностей там же;
- разности
электрических потенциалов поверхностей там же; ![]() - заряды ионов;
- заряды ионов; ![]() - постоянная Фарадея;
- постоянная Фарадея;
![]() - газовая постоянная;
- газовая постоянная;
![]() - температура.
- температура.
Проанализируем на основе уравнений (3), (4) различные
механизмы возникновения асимметрии мембран. Из этих соотношений следует, что
можно выделить три механизма возникновения асимметрии мембраны в отношении направления потока.
Во-первых, асимметрия может возникать в результате
различия коэффициентов химической активности компонентов на различных
поверхностях мембраны. Этому может способствовать также скин-слой.
Как известно, коэффициент химической активности из
соотношения, связывающего химическую активность (по которой производится расчет
химического потенциала) и мольную концентрацию компонента:
 . (5)
. (5)
Вторым
источником асимметрии может служить неравенство поверхностных плотностей заряда
мембраны. Этот эффект также стимулируется наличием скин-слоя.
Наконец, в-третьих, асимметрия может возникнуть за
счет обоих отмеченных механизмов, хотя может, наоборот, возникнуть конкуренция
этих механизмов, снижающая степень асимметрии.
Рассмотрим, как могут трансформироваться уравнения
переноса с учетом отмеченных явлений.
В отсутствие потенциалов поверхности можно
воспользоваться классическими условиями равновесия Доннана или условиями
электронейтральности [4].
Для двухкомпонентной
системы в этом случае можно записать:
![]() ,
(6)
,
(6)
![]() ,
(7)
,
(7)
![]() , (8)
, (8)
![]() , (9)
, (9)
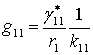 ,
, 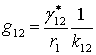 ,
(10)
,
(10)
 ,
, 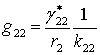 .
(11)
.
(11)
В соотношениях (6) – (11 приняты следующие
обозначения: ![]() - отношения концентраций компонентов потоках с обеих мембраны;
- отношения концентраций компонентов потоках с обеих мембраны;
![]() - числа ионов данного
типа в расчете на молекулу электролита;
- числа ионов данного
типа в расчете на молекулу электролита;
![]() .
.
Таким образом, при записи потока компонента через
мембрану, необходимо учитывать двоякий характер движущей силы процесса
переноса. сопровождающегося обратным осмосом. Это можно сделать с помощью следующего
феноменологического соотношения:
![]() ,
(12)
,
(12)
где ![]() - поток компонента через мембрану;
- поток компонента через мембрану; ![]() - коэффициент
внутренней молекулярной диффузии в мембране;
- коэффициент
внутренней молекулярной диффузии в мембране; ![]() - специальный
мембранный коэффициент, определяемый с учетом скин-слоя;
- специальный
мембранный коэффициент, определяемый с учетом скин-слоя; ![]() -плотность заряда
мембраны.
-плотность заряда
мембраны.
В любом случае, как и при обычной диффузии, поток
ионов данного вида внутри мембраны пропорционален градиенту концентрации в
мембране. В то же время, наличие градиента плотности заряда мембраны также
играет роль составляющей движущей силы процесса переноса.
Это означает также, знание отношения концентраций
компонента ![]() с обеих сторон
мембраны
с обеих сторон
мембраны ![]() для расчета процесса
в асимметричной не достаточно. В
качестве альтернативы управляющего
параметра в этом случае можно предложить фактор, введенный в [4]:
для расчета процесса
в асимметричной не достаточно. В
качестве альтернативы управляющего
параметра в этом случае можно предложить фактор, введенный в [4]:
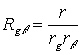 , где
, где
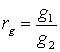 ,
, 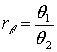 . (13)
. (13)
Предложенная модель позволяет учесть практически все
основные факторы, влияющие на перенос в асимметричных мембранах, и использует
по существу один эмпирический коэффициент ![]() - мембранный
коэффициент переноса с учетом скин-слоя. Это позволяет рекомендовать описанную
модель в качестве основы для организации экспериментальных исследований и
разработки методики расчета.
- мембранный
коэффициент переноса с учетом скин-слоя. Это позволяет рекомендовать описанную
модель в качестве основы для организации экспериментальных исследований и
разработки методики расчета.
Литература
1. Тимашев С.Ф. Физико-химия мембранных процессов.-
М.:Химия,1988,239 с..
2. Овчинников А.А., Тимашев С.Ф. Белый А.А. Кинетика
диффузионно-контролируемых химических процессов.- М.: Химия, 1986, 289 с.
3. Ясминов А.А. и др. Обработка воды обратным осмосом
и ультрафильтрацией.- М.: Стройиздат, 1978, 121 с.
4. Накагаки М. Физическая химия мемьран.- М.: Мир,
1991, 256 с.