Михайленко В.С.

Одесская государственная академия строительств и архитектуры

Сравнительный анализ нечеткого и ПИД – регуляторов при управлении объектами третьего и четвертого порядка

 

         В  последнее  время  в  теории   искусственного интеллекта и системах автоматизированного управления получают широкое распространение    нечёткие  алгоритмы  регулирования.  Нечеткие регуляторы,  построенные на основе нечетких множеств и нечеткой логики, в условиях неопределенности возмущающих воздействий, способны обеспечить более высокие показатели качества переходных процессов по сравнению с традиционными регуляторами [1]. Используя опыт, интуицию и знания эксперта − оператора,  возможно, оптимизировать  сложные  объекты  регулирования  без  проведения всесторонних  исследований по разработке классических  математических моделей. 

       Задача  создания  базы  знаний для нечеткого регулятора представляет собой  одну  из  ключевых  при построении нечеткой системы регулирования. Для её решения используются разные методы:  интервьюирование группы  операторов,  фиксирование  решений принимаемых  оператором  в  различных  ситуациях при дистанционном или ручном регулировании, анализ  желаемой траектории переходного процесса и т.д. [2].

       В представленной работе  проводится разработка  базы  знаний  нечеткого регулятора  на  основании анализе  характеристик  замкнутой  системы стабилизации. И апробация нечеткой САР с объектами третьего и четвертого порядка при действии на объект канала возмущения. 

Создание нечеткой системы регулирования разбивается на ряд этапов:   

1. Выбор желаемой характеристики переходного процесса.  В  качестве  примера  принята  траектория  САР  с  ПИД – регулятором  и  объектом  третьего порядка (рис. 1). Настройки регулятора рассчитаны методом Зиглера-Никольса. Измеряемыми параметрами являются  ошибка,  производная ошибки и управляющее воздействие - выход ПИД – регулятора (рис.2). 

 

Рис. 1 – САР с ПИД – регулятором

 

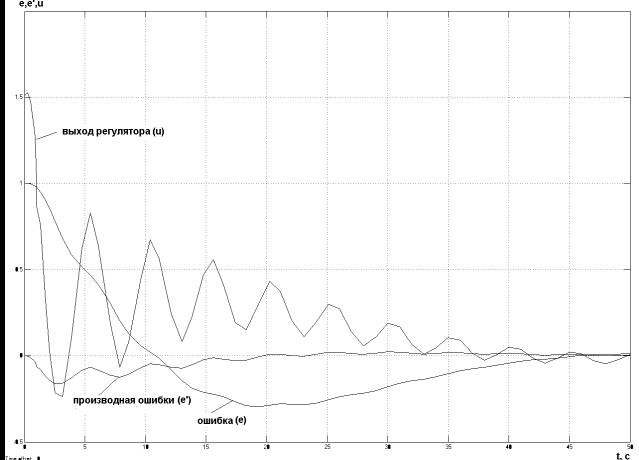
Рис.2 – Переходные процессы измеряемых параметров ПИД - регулятора

 

2. Фаззификация.

     При проведении фаззификации определяются нечеткие множества для ошибки е(t), производной ошибки е´(t), управляющего  воздействия U(t).

Числовой универсум определен исходя из рис.2. Вид, назване и количество функций принадлежности выбраны с помощью рекомендаций  [3]:

;;                                          ;;; ; EiE;  i = ; e (t) E,                                                  

где E – универсальное множество ошибок; e(t) – текущее значение ошибки в определенный момент времени; µi(ei(t)) – функция принадлежности к нечеткому множеству ei(t); NB – негативно большое (терм), NS – негативно среднее, NM – негативно малое, Z – нулевое, PS – положительно среднее, PM – положительно малое, PB – положительно большое  (рис.3)

    Аналогичным образом определяются нечеткие множества (функции принадлежности) для производной ошибки и управляющего воздействия (выхода нечеткого регулятора) (рис.4-5). Производная:  dE/dt  (e’m, (e’m (t))), m = 1, 2,…, n7, n7=7.  Управляющего воздействия (выход) регулятора: U  (um, (um (t))), m = 1, 2,…, n7, n7 = 7, где e(t) = z(t) – y(t),  e’ (t) = e (t).                                     

   μ(е)

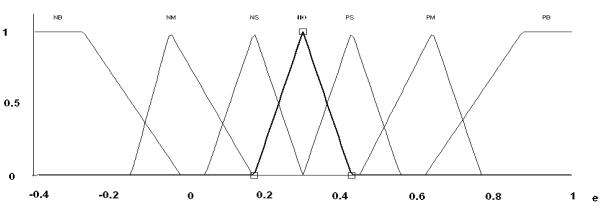
Рис. 3 -  Функции принадлежности « ошибка»

3. На следующем этапе производится составления продукционных правил для базы знаний нечеткого регулятора в виде следующих суждений (табл. 1):

        ЕСЛИ e(t) NM , И  e´(t) NM, ТО U(t) NM, ИНАЧЕ;

ЕСЛИ e(t) NB, И  e´(t) NB, ТО U(t) NB  и т.д.  

                                                                                                                

μ(e’)  

е’

Рис. 4 - Функции принадлежности  « производная ошибки»

μ(u)  

 u         

Рис. 5 - Функции принадлежности  « управляющее воздействие»

                                                                                  Таблица 1

База знаний

Ошибка e(t)

Производная  ошибки,  e´(t)

NB

NS

NM

 

Z

 

PM

 

PS

 

PB

U(t)- управление

NB

NB

NB

NB

OS

Z

PM

PS

NS

NS

NS

NS

NM

PM

PM

PS

NM

NS

NM

NM

Z

Z

PM

PS

Z

NS

NM

NM

Z

PM

PM

PS

PM

NM

NM

Z

Z

PM

PM

PS

PS

NM

NM

Z

PM

PS

PS

PS

PB

NS

NM

Z

PS

PS

PB

PB

4.Этап дефаззификации, по каналу регулирования, проводится методом центра тяжести:   U= 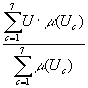     5. Апробация  нечеткой базы знаний в среде MatLab (Simulink) представлена на рис.6.

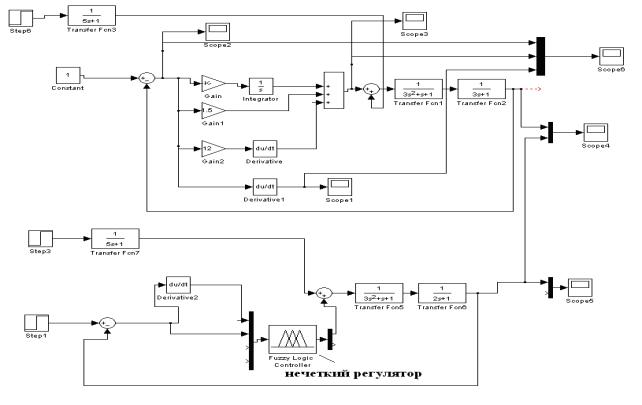
Рис.6- САР объектом третьего порядка  с ПИД и нечетким регуляторами  по каналам задания и возмущения

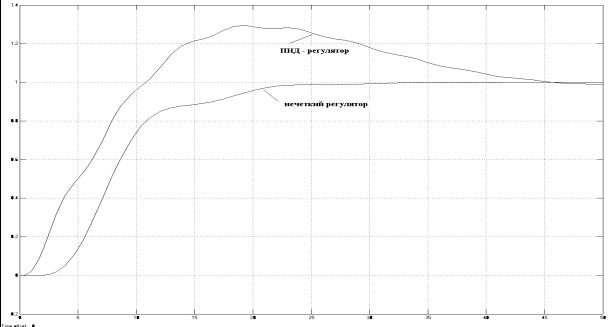
Заключение. Анализ рис.7 показал что,  время регулирования нечеткой системы на 20 секунд меньше чем у ПИД – регулятора, также у нечеткой САР отсутствует первое отклонение, что свидетельствует о ее преимуществе. При усложнении объекта (введение фактора неопределенности) с передаточной функцией вида W(s) = (1/3S2+s+1)*(1/ 2S2+s+1) переходный процесс у нечеткой САР достигает заданного значения за 30 секунд, а ПИД – регулятор требует перерасчета новых значений настроек т.к. его процесс расходящийся (рис.8). Таким образом, в условиях неопределенности и динамики свойств объект регулирование, использование нечетких САР является предпочтительней по сравнению с типовыми системами регулирования      

Z (t)                      

t, c

Рис.7 – Переходные процессы по каналу задания при действии возмущения

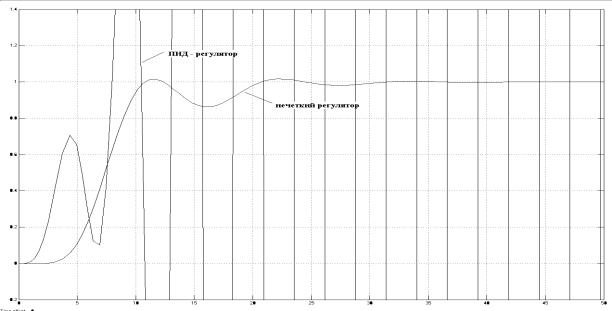 t, c

Рис.8 – Переходные процессы при усложнении порядка объекта

Литература

1.     Леоненков А. Ю. Нечеткое моделирование в среде Matlab и fuzzyTech. - С. - Птб.: БХВ, 2003. ─  720 с.

2.     Золотухин Ю.Н., Кущ А.В. Вариант построения базы правил для нечеткого контроллера./ ermak.cs.nstu.ru

3.     Алиев Р.А., Церковный А.Э., Мамедова Г.А. Управление производством при нечеткой исходной информации. М.: Энергоиздат. 1991. – 234 с