Математика / 4. Прикладная математика
Бондаренко А. Ю., Крылов В. Н., Полякова М. В.
Одесский национальный политехнический университет,
Украина.
Метод предварительной обработки
изображений,
пораженных блочным шумом.
I. ВВЕДЕНИЕ
Сжатие
информации является на сегодняшний день очень важной проблемой, так как все
большую популярность приобретают сетевые технологии. Это связано с
глобализацией мировой сферы информационных технологий. Одним из наиболее
распространенных объектов для передачи по сети является изображение или
последовательность изображений. Поэтому были созданы алгоритмы сжатия
изображения с потерями, одним из которых является JPEG.
В случае указания слишком большого коэффициента сжатия
(больше 50), на этапе квантования в алгоритме сжатия JPEG получается матрица, в
которой существенными оказываются только элементы, отвечающие за самые низкие
частоты. Это означает, что при восстановлении в области изображения, соответствующей
каждой подматрице (8х8 пикселей) присутствует только низкочастотная составляющая
изображения (плавные переходы), а мелкие детали и границы потеряны. В
результате получается изображение, искаженное блочным шумом.
Типичным примером таких изображений являются кадры из
кинофильмов, сжатых блочными кодеками (DivX, MPEG) при высокой степени сжатия
(рис. 1, 2).
|
|
|
|
Рисунок 1 – исходное, несжатое изображение. |
Рисунок 2 – чрезмерно сжатое изображение. |
Удаление блочного шума с изображения, подвегнутого
высокой степени сжатия проводится аппаратными средствами на этапе
восстановления изображения. Это приводит к увеличению ресурсоемкости процесса
кодирования и декодирования изображения. Поэтому задача удаления блочного шума
на восстановленном изображении методами предварительной обработки, реализуемых
программными средствами, является актуальной.
Адекватным математическим аппаратом для представления
и обработки блочного шума на изображении является дискретное вейвлетное
преобразование (ДВП), коэффициенты которого содержат информацию о содержании
блоков изображения разного размера. Необходимость в такой информации возникает
вследствие того, что в алгоритме сжатия JPEG могут
использоваться блоки изображения размером 8х8, 16х16 и др.
Целью работы является разработка и исследование метода
удаления блочного шума на изображениях в пространстве вейвлет преобразования
для повышения качества и эффективности предварительной обработки.
В процессе достижения поставленной цели выполнялось
моделирование блочного шума на изображении. Для решения этой задачи
использовалось представление изображения с помощью фрактального броуновского
процесса, что является адекватным для реальных изображений [2, 3, 4].
В работе [4] было получено приближение фрактального
броуновского процесса с помощью коэффициентов ДВП.
Для вычисления вейвлет коэффициентов использовалась формула
|
|
(1) |
где N(0,1) – гауссовский шум с нулевым
математическим ожиданием, и единичной дисперсией,
H2 – параметр, принимающий значения из диапазона [0, 1],
![]() - параметр масштаба.
- параметр масштаба.
Коеффициенты аппроксимации на максимальном уровне ДВП
занулялись:
|
|
(2) |
В качестве анализирующего вейвлета использовался
вейвлет Хаара.
|
|
(3) |
Предлагается следующий метод генерации блочного шума:
1)
задается количество
уровней ДВП и параметр H2
(например, количество уровней – 4, H2
= 0.5);
2)
создается коллектор
шума: матрица из нулей, размера M/2p х N/2p, где p -
количество уровней ДВП, M,N – размеры изображения, на которое будет
накладываться шум. Этот коллектор принимается за матрицу коэффициентов;
3)
в качестве текущего
уровня выбирается уровень с максимальным номером (в данном случае – 4);
4)
генерируются вейвлет коэффициенты
по формуле (1), где j – номер текущего уровня; для использования двумерного обратного
ДВП необходимы три матрицы вейвлет коэффициентов: горизонтальных, вертикальных
и диагональных;
5)
коллектор шума, в
качестве матрицы коэффициентов аппроксимации, и три сгенерированные матрицы вейвлет
коэффициентов подаются на вход обратного ДВП; результат записывается в
коллектор шума;
6)
осуществляется переход
на следующий уровень и повторяется действие 5, а в качестве вейвлет коэффициентов
подаются нулевые матрицы;
7)
результат, накопленный в
коллекторе шума, суммируем с исходным изображением.
Такой подход позволяет получить блочный шум с
нормально распределенными значениями интенсивности. Коррелированность значений
интенсивности шума определяется величиной Н2, а размер блоков –
количеством уровней ДВП.
Предлагается метод подавления блочного
шума на изображениях. Он заключается в следующем:
1)
исходное изображение
подвергается прямому ДВП, в результате чего получается матрица коэффициентов аппроксимации
и три матрицы вейвлет коэффициентов;
2)
если заданное количество
уровней ДВП больше 1, матрица коэффициентов аппроксимации снова раскладывается
с помощью ДВП;
3)
после ДВП на необходимое
количество уровней к матрице коэффициентов аппроксимации применяется локальная
адаптивная фильтрация [1];
4)
из отфильтрованной
матрицы коэффициентов аппроксимации и матриц вейвлет коэффициентов
реконструируется исходное изображение с помощью обратного ДВП;
5)
в результате обратного
ДВП изображения, получается отфильтрованное изображение.
Дополнительно вычисляется среднее взвешенное
изображение по формуле
|
Im
= (2 * In + Imed) / 3 , |
(4) |
где Im
– средневзвешенное изображение,
In – изображение, полученное с помощью разработанного
метода предварительной обработки,
Imed – изображение, полученное с помощью медианной
фильтрации.
II. ЭКСПЕРИМЕНТАЛЬНЫЕ
ИССЛЕДОВАНИЯ
Для оценки эффективности предварительной
обработки изображения использовался коэффициент уменьшения энтропии, так как
снижение уровня помех приводит к уменьшению энтропии изображения [5]:
|
|
(5) |
где H –
энтропия зашумленного изображения;
|
|
(6) |
где n –
количество значений интенсивности изображения;
P(xi) – вероятность появления значения интенсивности xi.
HP – энтропия изображения после предварительной
обработки.
Показателем
качества служила характеристика ![]() , основанная на среднеквадратичном отклонении [5]:
, основанная на среднеквадратичном отклонении [5]:
|
|
(7) |
где ![]() – тестовое изображение;
– тестовое изображение;
![]() – изображение,
которое получено после предварительной обработки;
– изображение,
которое получено после предварительной обработки;
![]() – зашумленное изображение.
– зашумленное изображение.
Экспериментальные исследования предложенного метода
предварительной обработки изображений были проведены на нескольких тестовых
изображениях, на которые был наложен блочный шум. Специфика моделирования блочного
шума такова, что размер блоков зависит от количества уровней ДВП в методе
генерации блочного шума, а именно:
|
|
(8) |
где N –
длина стороны квадратного блока (в пикселях);
р – количество уровней ДВП.
Для каждого изображения генерировался блочный шум со
следующими показателями коэффициента H2
: 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0 в формуле (1). Фильтрация
проводилась разработанным методом и медианным фильтром.
Первое изображение, на котором проводились
эксперименты – черно-белый перепад размером 256х256 точек.
|
а) |
б) |
в) |
|
г) |
Рисунок 3 – изображение, зашумленное блочным шумом с
параметром H2, равным 1.0 (а), изображение, полученное с помощью
разработанного метода предварительной обработки изображений, пораженных
блочным шумом (б), изображение, полученное после фильтрации медианным
фильтром с размером апертуры 9х9 (в), средневзвешенное изображение по формуле
(4) (г). |
|
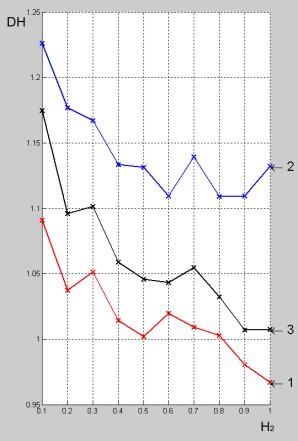
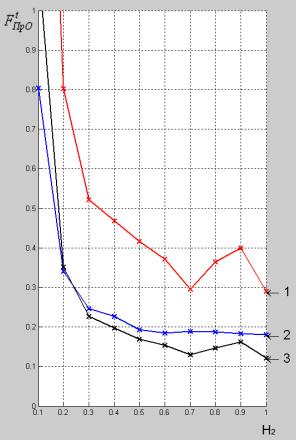
На рис. 4 и 5 изображены графики показателей
эффективности и качества фильтрации. Отметки возле графиков обозначают: 1 –
разработанный метод, 2 – медианная фильтрация, 3 – средневзвешенное изображение.
Как мы видим, на модельном изображении, состоящем из двух областей,
эффективность разработанного метода ниже, чем двух остальных, однако по
качеству этот метод в среднем на 25-30% превышает показатели двух других
методов.
|
|
|
|
Рисунок 4 – график показателя эффективности. |
Рисунок 5 – график показателя качества. |
Однако следует заметить, что такого рода модельное
изображение не отражает действительных условий работы метода предварительной
обработки. Поэтому эксперименты были проведены на других изображениях, более
близких к реальным.

Рисунок 6 – тестовое изображение №2. [1]
|
а) |
б) |
в) |
||
|
г) |
Рисунок 7 – тестовое изображение №2, зашумленное
блочным шумом с параметром H2
равным 0.5 (а), изображение, полученное в результате применения разработанного
метода предварительной обработки изображений, пораженных блочным шумом (б),
изображение, полученное после фильтрации медианным фильтром с размером
апертуры 9х9 (в), средневзвешенное изображение по формуле 4 (г). |
|||
|
|
|
|||
|
|
|
|
||
|
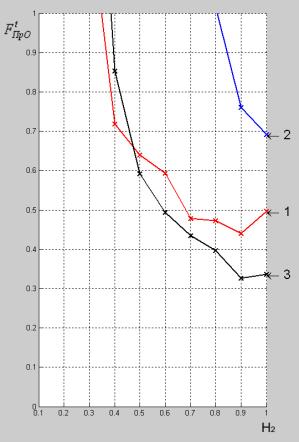
Рисунок 8 – график показателя эффективности. |
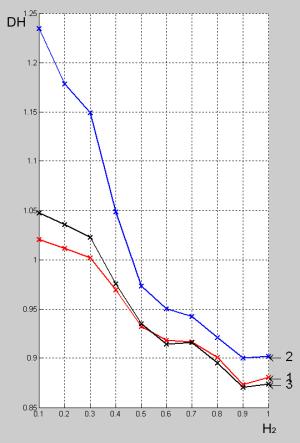
Рисунок 9 – график показателя качества. |
|
||
Из этого эксперимента видно, что медианная
фильтрация лучше справляется с блочным шумом на равномерных участках (что и
наблюдалось на тестовом изображении №1), однако уничтожает малоразмерные
объекты на изображении и размывает границы крупных объектов. Разработанный
метод хорошо себя показывает вблизи границ объектов (в следствие применения локальной
адаптивной фильтрации). Средневзвешенное результатов фильтрации этих двух
методов позволяет улучшить качество фильтрации на 20-40% по сравнению с
предложенным методом и на 100-120% по сравнению с медианной фильтрацией,
сохраняя приемлемый уровень эффективности фильтрации (рис. 8).
III. ПРАКТИЧЕСКОЕ ИСПОЛЬЗОВАНИЕ ПРЕДЛОЖЕННОГО МЕТОДА
Разработанный метод подавления блочного
шума использовался для предварительной обработки изображений, к которым был
применен алгоритм блочного сжатия с коэффициентом сжатия 100. На рис. 10,б
приведено изображение с блочным шумом (p = 4, H2 = 0.8). После применения разработанного метода
подавления блочного шума было получено изображение 10,в.
|
а) |
б) |
|
в) |
Рисунок 10 – пример работы метода подавления
блочного шума. Исходное изображение (а), искаженное изображение (б) и
изображение после применения метода предварительной фильтрации (в). |
IV. ВЫВОДЫ
Предложенный метод подавления блочного шума
целесообразно использовать для предварительной обработки изображений,
полученных при чрезмерном сжатии с помощью блочных алгоритмов сжатия изображений,
таких как JPEG. Такая
предварительная обработка изображений позволяет сохранить высокое качество
востановленных изображений, которые были подвергнуты сильному сжатию.
ЛИТЕРАТУРА
1.
Гонсалес Р., Вудс Р.
Цифровая обработка изображений / Пер. с англ. – М.: Техносфера, 2005. – 1072 с.
2.
Davis A., Marshak A.,
Gerber H., Warren W. Multifractal characterizations of nonstationary and
intermittency in geophysical fields: Observed, retrieved or simulated // Jornal
of Geophysical Research. — 1994. — V. 99, № D4. — P. 8055 — 8072.
3.
Davis A., Marshak A.,
Clothiaux E. Anisotropic multi-resolution analysis in 2D, Application to
long-range correlations in cloud mm-radar fields // Proceeding of SPIE reprint,
Wavelet applications VI. — 1999. — V. 3723. — P. 194 — 207.
4.
Flandrin P. Wavelet
analysis and synthesis of fractional Brownian motion // IEEE Transactions on
Information Theory. — 1992. — V. 38, № 2. — P. 910-920.
5.
Абакумов В.Г., Крылов
В.Н., Антощук С.Г. Повышение эффективности обработки образной информации в
автоматизированных системах // Электроника и связь: Темат. вып. “Проблемы
электроники”. – 2005. – Ч. 1. – С. 100–105.


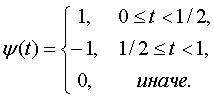
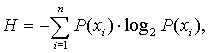
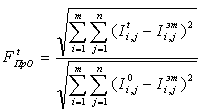 ,
,