Каллаур Н.А., Корчук О.В.

Брестский государственный университет имени А.С. Пушкина

ПРИМЕНЕНИЕ ЗАДАЧНЫХ ТЕХНОЛОГИЙ В ОБУЧЕНИИ МАТЕМАТИКЕ

Примерно половина уроков математики в средней школе отводится решению математических задач и выполнению упражнений. При решении математических задач учащиеся усваивают многие математические понятия, овладевают математической символикой, обучаются проведению доказательств.

Методы нахождения решений и психическая деятельность, связанная с поиском решения, во многом сходны как в жизненных или производственных задачах, так и в школьных (по математике, физике, химии). Поэтому ознакомление учащихся с методами поиска решений является средством не только улучшения учебных навыков, но и воспитания учащихся, подготовки их к будущей производственной деятельности, к жизни.

С применением математических задач можно добиваться многих дидактических целей: актуализация знаний и изучение теоретических вопросов математики (новых понятий, методов, теорем), закрепление только что приобретенных теоретических знаний, формирование умений и навыков, повторение ранее изученного материала, осуществление контроля за усвоением математических знаний.

Для закрепления нового материала, отработки изученных понятий и свойств разработано достаточное количество систем упражнений, ни один учебник не обходится без математических задач.

В учебно-методический комплекс входят сборники задач, с помощью которых можно без труда организовать проверочные и контрольные самостоятельные работы. Осуществить повторение пройденного за весь курс математики и подготовиться для сдачи экзаменов и ЕГЭ помогут сборники тестовых заданий и «практикумы по математике». Однако, при поиске систем задач и упражнений, позволяющих осваивать новый теоретический материал, возникают значительные трудности.

Разработка полноценных задачных комплексов для изучения теории занимает у учителя большое количество времени, поэтому целью нашего исследования стала разработка системы задачных упражнений для изучения математики в старших классах.

Обучение математике регламентировано рамками учебного времени, программой, поэтому необходимо тщательно отбирать материал для изучения через задачи. При разработке урока по изучению новой темы учитель сталкивается с проблемой выбора способа введения новых понятий, доказательства теорем; немаловажно обучить учащихся построению алгоритмов решения задач. Продемонстрируем возможности задачных технологий на примере изучения алгебры в 11 классе.

Например, при анализе темы о введении понятия логарифма в 11 классе можно выделить следующие этапы изучения материала:

1. Формирование понятия «логарифм числа а по основанию b».

2. Нахождение простейших логарифмов по определению.

3. Формулирование свойств логарифма.

4. Доказательство теорем о правилах вычисления логарифмов.

5. Применение правил вычисления логарифмов.

Исходя из общих задач (этапов), строится необходимая система задач для изучения данного теоретического материала.

Для актуализации знаний при введении понятия логарифма можно предложить учащимся решить ряд показательных уравнений, с которыми они справятся без труда, например, 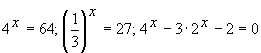. Следующая задача должна быть на порядок сложнее и на основе имеющихся знаний «нерешаемая», например, решить уравнение .

Решать показательные уравнения учащиеся уже умеют, однако они сталкиваются с проблемой, что не всегда легко можно подобрать число, которое будет являться корнем таких уравнений. Чтобы убедиться, что такое число действительно существует, учащимся предлагается решить задачу графически.

Рассмтрим функцию y=f(x), где f(x) =.

Функция y=f(x) возрастает на всей числовой прямой, следовательно, по теореме о корне уравнения f(x)=3 имеет единственный корень.

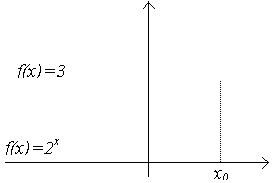
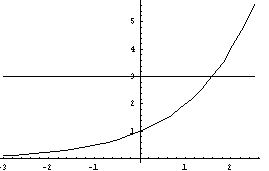
Рисунок 1

Школьники убеждаются, что корень уравнения есть, но возникает вопрос: «Как назвать такой корень?». В привычных для них обозначениях назвать и записать корень уравнения нельзя. Тогда учитель сообщает учащимся, что показатель степени, в которую нужно возвести число 2 чтобы получить число 3, принято нызывать логарифом числа 3 по основания 2, и обозначать log₂3.

Далее учащимся предлагается решить по аналогии показательное уравнение в общем виде , при решении которого, дается определение логарифма в общем виде.

При изучении свойств логарифма также используется принцип перехода от частных задач к общим. Например, при изучении свойств логарифма, учащимся сначала предлагается вычислить логарифм в частных случаях, и только после того как будет замечена закономерность, выдвигается гипотеза о существовании свойств логарифма, которая доказывается с помощью учащихся. Затем доказанное утверждение формулируется как свойство, тут же учитель заостряет внимание учащихся на значимости обнаруженного свойства (выделяет его цветом, обводит в рамку для эффективного запоминания).

Найти 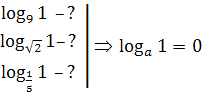, т.к. при любом а.

Найти 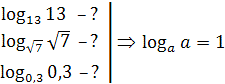, т.к. при любом а.

Одним из способов обучения доказательствам через задачи является замена теоремы задачей, обязательной для решения. Теоремы, соответствующие некоторым правилам вычисления логарифмов, могут быть заменены следующими задачами.

Найдите , если .

Верно ли, что для любого ?

Упростите .

Найдите , если p, q, log_bc равны соответственно 16, 4, 7.

После решения предложенных задач и обобщения некоторых решений формулируются соответствующие теоремы, доказательство которых не составит сложностей для учащихся.

Таким образом, применение задачной технологии обучения математике позволяет учащимся более эффективно и сознательно овладевать новыми знаниями, умениями и навыками. При этом у учащихся наблюдается более глубокое понимание учебного материала, развивается мышление, проявляется творчество, воспитывается усидчивость, трудолюбие, настойчивость в достижении цели и самостоятельность, последнее особенно важно для старшеклассников.