*99598*

Isotopetronics: Fundamentals and Applications.

L.M. Zhuravleva,

Railway University, Obrastzova Street 9, Moscow 127994, Russia.

V.G. Plekhanov,

Computer Science College, Erika Street 7a, Tallinn, 10416, Estonia.

Isotopetronics is a new branch of the nanoscience. The present report is devoted to brief description the fundamentals and the main applications this new direction: isotope memory information and solid state processor for quantum computers.

Introduction.

The experience of the past shows that throughout constant technology improvement electronics (optoelectronics) has become more reliable, faster, more powerful, and less expensive by reducing the dimensions of integrated circuits. These advantages are the driver for the development of modern microelectronics. The long - term goal of this development will lead to nanoelectronics. Advancing to the nanoscale is not just a step toward miniaturization, but requires the introduction and consideration of many additional phenomena. At the nanoscale, most phenomena and processes are dominated by quantum physics and they exhibit unique behavior. Nanotechnology includes the integration of manmade nanostructures into larger material components and systems (see, e.g. [1]). Importantly, within these larger scale systems, the active elements of the system will remain at nanoscale.

Low - dimensional structures have become one of the most active research in nanoscience and nanotechnology.

The seminal works of Esaki and Tsu [2] and others on the semiconductor superlattice stimulated a vast international research effort to understand the fabrication and electronic properties of superlattice, quantum wells, quantum wires and quantum dots (see, for example, [3 - 6]). The dimensional scale of such samples is between 10 and 100 nm are subject of nanoscience - is a broad and interdisciplinary field of emerging research and development. Nanoscience and nanotechnology are concerned with materials, structures, and systems whose components exhibit novel and significantly modified physical, chemical properties due to their nanoscale sizes. New direction of nanoscience is isotopetronics, who is studied the more low - dimensional size, as a rule the sizes of the sample of isotopetronics compare to the atomic size. Nuclear technology - neutron irradiation [7] - is very useful method to preparing low - dimensional structure: quantum wells, quantum wires and quantum dots [8]. A principal goal of isotopetronics as new directions of the nanotechnology is to control and exploit their new properties in structures and devices at atomic, molecular and supramolecular levels. The minituarization required by modern electronics is one of the driving forces for isotopetronics - new direction of nanotechnology (see, also [9]).

Results and discussion.

Semiconducting crystals (C, Si, Ge, α - Sn) with diamond - type structure present ideal objects for studying the isotope effect by the Raman light - scattering method. At present time this is facilitated by the availability of high - quality crystals grown from isotopically enriched materials (see, e.g [10] and references therein). In this part our understanding of first - order Raman light scattering spectra in isotopically mixed elementary and compound (CuCl, GaN, GaAs) semiconductors having a zinc blende structure is described. Isotope effect in light scattering spectra in Ge crystals was first investigated in the paper by Agekyan et al. [ 11]. A more detailed study of Raman light scattering spectra in isotopically mixed Ge crystals has been performed by Cardona and coworkers [10].

It is known that materials having a diamond structure are characterized by the triply degenerate phonon states in the Γ point of the Brillouin zone (k = 0). These phonons are active in the Raman scattering spectra, but not in the IR absorption one [28]. Figure 1^a demonstrates the dependence of the shape and position of the first - order line of optical phonons in germanium crystal on the isotope composition at liquid nitrogen temperature (LNT) [12].

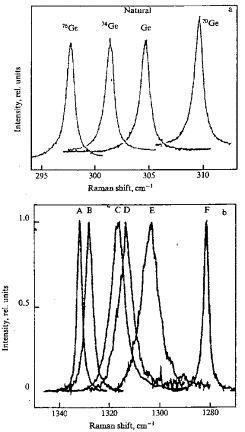Fig. 1. a - First - order Raman scattering spectra Ge with different isotope contents [10] and b - First - order Raman scattering in isotopically mixed diamond crystals ¹²C_x¹³C_1-x. The peaks A, B, C, D, E and F correspond to x = 0.989; 0.90; 0.60; 0.50; 0.30 and 0.001 (after [15]).

The coordinate of the center of the scattering line is proportional to the square root of the reduced mass of the unit cell, i.e. √M. It is precisely this dependence that is expected in the harmonic approximation. An additional frequency shift of the line is observed for the natural and enriched germanium specimens and is equal, as shown in Ref. [10] to 0.34 ± 0.04 and 1.06 ± 0.04 cm⁻¹, respectively (see, e.g. Fig. 7 in Ch. 4 of Ref. [14]).

First - order Raman light - scattering spectrum in diamond crystals also includes one line with maximum at ω_LTO(Γ) = 1332.5 cm⁻¹. In Fig. 1_b the first - order scattering spectrum in diamond crystals with different isotope concentration is shown [15]. As shown below, the maximum and the width of the first - order scattering line in isotopically - mixed diamond crystals are nonlinearly dependent on the concentration of isotopes x. The maximum shift of this line is 52.3 cm⁻¹, corresponding to the two limiting values of x = 0 and x = 1. Analogous structures of first - order light scattering spectra and their dependence on isotope composition has by now been observed many times, not only in elementary Si, and α - Sn, but also in compound CuCl and GaN semiconductors (for more details see reviews [10, 16]). Already short list of data shows a large dependence of the structure of first - order light - scattering spectra in diamond as compared to other crystals (Si, Ge). This is the subject detailed discussion in [17]. Second - order Raman spectra in natural and isotopically mixed diamond and LiH - LiD have been studied and rather detailed described in reviews (see, e.g. [17]).

Isotopic substitution only affects the wavefunction of phonons; therefore, the energy values of electron levels in the Schrödinger equation ought to have remained the same. This, however, is not so, since isotopic substitution modifies not only the phonon spectrum, but also the constant of electron-phonon interaction (see, e.g. [16]). It is for this reason that the energy values of purely electron transition in molecules of hydride and deuteride are found to be different ([16] and references therein). This effect is even more prominent when we are dealing with a solid [18]. Intercomparison of absorption spectra for thin films of LiH and LiD at room temperature revealed that the longwave maximum (as we know now, the exciton peak [16]) moves 64.5 meV towards the shorter wavelengths when H is replaced with D. For obvious reasons this fundamental result could not then receive consistent and comprehensive interpretation, which does not be little its importance even today. As will be shown below, this effect becomes even more pronounced at low temperatures (see, also [17]).

The mirror reflection spectra of mixed and pure LiD crystals cleaved in liquid helium are presented in Fig. 2.

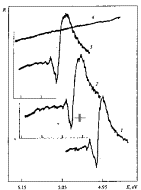
Fig. 2. Mirror reflection spectra of crystals: 1 - LiH; 2 - LiH_xD _1-x; 3 - LiD; at 4.2 K. 4 - source of light without crystal. Spectral resolution of the instrument is indicated on the diagram (after [7]).

For comparison, on the same diagram we have also plotted the reflection spectrum of LiH crystals with clean surface. All spectra have been measured with the same apparatus under the same conditions. As the deuterium concentration increases, the long-wave maximum broadens and shifts towards the shorter wavelengths. As can clearly be seen in Fig. 6, all spectra exhibit a similar long-wave structure. This circumstance allows us to attribute this structure to the excitation of the ground (Is) and the first excited (2s) exciton states. The energy values of exciton maxima for pure and mixed crystals at 2 K are presented in Table 17 of Ref. [19]. The binding energies of excitons E_b, calculated by the hydrogen-like formula, and the energies of interband transitions E_g are also given in Table 17 of ref. [19]. Going back to Fig. 2, it is hard to miss the growth of Δ₁₂, [18], which in the hydrogen-like model causes an increase of the exciton Rydberg with the replacement of isotopes (see Fig. 90 in [16]). When hydrogen is completely replaced with deuterium, the exciton Rydberg (in the Wannier-Mott model) increases by 20% from 40 to 50 meV, whereas E_g exhibits a 2% increase, and at 2 ÷ 4.2 K is ΔE_g = 103 meV. This quantity depends on the temperature, and at room temperature is 73 meV, which agrees well enough with ΔE_g = 64.5 meV as found in early the paper of Kapustinsky et al. [20]. Isotopic substitution of the light isotope (³²S) by the heavy one (³⁴S) in CdS crystals [19] reduces the exciton Rydberg, which was then attributed to the tentative contribution from the adjacent electron bands (see also [19), which, however, are not present in LiH (for the details see e.g. reviews [14, 10, 16]).

Further we briefly discuss the density of optical states in different size - structures: one - , two and three - dimension (see, also [22]). Traditionally, microelectronics is based on scaling towards smaller structures. When the dimension of these structures reach the nanometric scale, microelectronics has already transformed to nanoelectronics. As was mentioned above, new directions of nanoscience is isotopetronics, who is studied the more low - dimensional size, as a rule the sizes of the sample of isotopetronics compare to the atomic size. The band diagram of a material depends on its crystal structure and on the material wavefunction of the electrons (see, e.g. [22]). The band diagram reveals the energy level that can be occupied.. The density of states (DOS) of these levels depend on the size of the crystal. An extensive three - dimensional body produces a three - dimensional k - space. The energy E of the electrons can be derived from solid - state physics as [22]:

E = ((ℏ²)/(2m))(k_x² + k_y² + k_z²) = ((ℏ²)/(2m))∣k∣². (1)

With respect to the three - dimensional k - space the possible states can be expressed as:

S = ((V_T)/(3π²))(((2mE)/(ℏ²)))^3/2. (2)

The DOS follows as:

((dS)/(dE)) = √2((V_Tm^3/2)/(π²ℏ²))√E. (3)

The DOS is proportional to the square root of the energy of the electrons. This function describes the well - known Bolzman relation of classical physics (see, also Fig. 3). A three - dimensional relatively large ashlars (3D potential well) has a steady √E characteristic for the DOS, whereas the DOS characteristics becomes discontinuous if at least a single dimension is scaled down to the domain of the material wavelength of an electron. This leads to quantum layers (2D potential well) and appears, e.g. in the inversion layer of a metal - oxide - semiconductor transistor [22]. Further steps lead to the quantum wire (1D potential well and a quantum dot (0D potential well). an electron space that is limited in one direction leaves an unlimited two - dimensional k - space for the electron. In this case of a quantum layer the energy of the particle is:

E = ((ℏ²)/(2m))(k_x² + k_y²) + E_i. (4)

Along the reduced dimension only states that match with the wavelength of the electrons can appear. Therefore, dicrete energy levels E_i appear. Because of the two - dimensional k - space the DOS S is directly proportional to E. If this expression is derived to E, dS/dE is independent of the energy (see, Fig. 3).

A further step leads to the so - called quantum wire, which leaves only one dimension of freedom to the electron. Consequently, the energy can be expressed as:

E = ((ℏ²)/(2m))(k_x² ) + E_in. (5)

Under this condition the DOS is for one - dimensional k - space inversely proportional to the square root of the energy. A restriction of all three dimensions of the DOS only discrete lines can appear,

E = E_imn. (6)

In this case the DOS shows only discrete lines, similar to a hydrogen atom or a molecule (see, Fig. 3). Such a quantum dot can be realized from a small semiconductors columns.

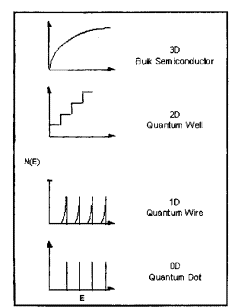
Fig. 3. Density of electronic states as a function of structure size.

In general, the lateral dimensions are adjusted so that the energy value of an electron is about one eV. The third dimension depends on a very thin epitaxial layer [22]. With respect to this dimension the electrons own at least twenty eV. This result in a clearly arranged energy spectrum since vertical energy levels only appear at higher energy levels. This arrays can be tuned to desired wavelengths and emit sufficient power for laser applications (see, also below). Detailed description of the low - dimensional structures of isotope - mixed crystals can be found in Refs. [22 - 23].

The knowledge gained in above discussion makes it possible to consider and analyze a variety of different nanostructure devices. In this part we consider electronic and optical devices. Some of these mimic well - known microelectronic devices but with small dimensional scales. This approach applications to devices with shorter response times and higher operational frequencies that operate at lower working currents, dissipate less power, and exhibit other useful properties and enhanced characteristics. Such example include, in the first step, the field effect transistors will be consider below. On the other hand, new generations of the devices are based on new physical principles, which can not realized in microscale devices. Among these novel devices are the resonant - tunneling devices described in next section, and single - electron - transistor as well as optoelectronic devices (light - emitting diodes and lasers).

As is well - known the diodes are simplest electronic devices, for which the current is controlled by the diode bias and vice versa. A useful function can be performed mainly due to nonlinearity of current - voltage dependences. In contrast, in three - terminal devices known as transistors there exist the possibility of controlling the current through two electrodes by varying the voltage or the current through third electrode. Below we briefly describe the field effect transistors (FETs) on the base of the nanowires. Nanowire FETs can be configurated by depositing the nanomaterial onto an insulating substrate surface, and making source and drain on the ends nanowire. Fig. 4 illustrates this approach. There , we show a schematic diagram of a Si - nanowire FET with the nanowire, the metal source and drain electrodes on the surface of the SiO₂/Si substrate (see, also [22]).

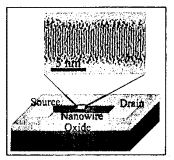
Fig. 4. A schematic diagram of a Si - FET with nanowire, the metal source, and drain electrodes on the surface of a SiO₂/ Si substrate (after [25]).

This approach may serve as the basis for hybrid electronic systems consisting of nanoscale building blocks integrated with more complex planar silicon circuitry [6]. We should note that an extremely small FET may be built on the basis of carbon nanotube. In conclusion of this part we have noted that the nanowire devices discussed here have great potential for applications in nano - and optoelectronics.

The so - called single electronics [22 - 26] appeared in the late 1980s, is at present time a tremendously expanded research field covering future digital and analog circuits, metrological standards, sensors, and quantum information processing and transfer [6]. The basic device, called a single electron device (SED), literally enables the control of electrons on the level of an elementary charge. There are rich varieties SEDs (see, e.g. [22] and references therein), but the operation principle of all SED is basically the same (see, Fig. 5).

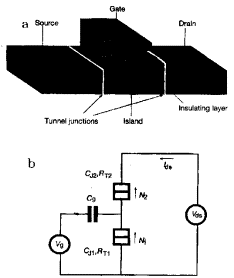Fig. 5. The single electron tunneling transistor (SET). a - Simplified three - dimensional structure of the SET. The channel of the FET is replaced here by a sandwich consisting of a nanoscal metal electrode (island), which is connected to the drain and the source by tunnel junctions. AS in FET, a gate electrode influences the island electrostatically. b - Circuit diagram of the SET. The square box symbol represents a tunnel junction, and integers N₁ and N₂ denote the numbers of electrons having through the two junctions Each junctions is characterized by its capacitance and its tunnel resistance (after [24]).

SEDs rely on a phenomenon that occurs when electrons are to enter a tiny conducting material. When the tiny conducting material, or metallic "island", is extremely small, the electrostatic potential of the island significantly increases even when only one electron enters it. For example, for a nanometer scale island having a capacitance C of, say, 1 aF (10⁻¹⁸F), the increase in the voltage, which is e/C with e = 1.6 ⋅ 10⁻¹⁹ C, reaches 16 mV. This is much larger than the thermal noise voltage at room temperature, 25.9 mV. Coulomb repulsion prevents additional electrons from entering the island unless the island potential is intentional lowered by an external bias. If the island potential is lowered gradually, the other electrons can enter the island one by one with negligibly small power dissipation .

Fig. 6. Single - electron transistor on the base of the MOP with double block (after [22]).

The single - electron transistor works as follows (Figs. 6 - 7). The electron transfer is determined by two factors: the Coulomb charging of the dot and the quantized energy levels in the dot (see above).

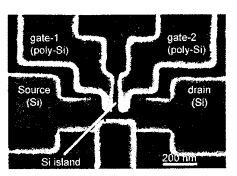
Fig. 7. A scanning electron microscope image of a single electron transistor (after [25]).

If the drain is biased with respect to the source, an electric current occurs in the regime of single - electron transfer. By applying the voltage to the gate and changing the QD parameters, one can change the conditions of electron tunneling and affect the source - drain current. Examples of modulation of the conductance in single - electron transistors by the gate voltage are presented in Fig. 8.

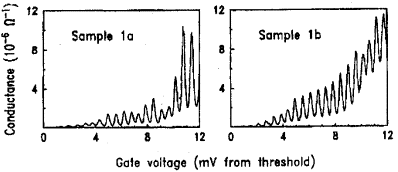
Fig. 8. Conductance as a function of V_g for two samples with the same geometry (after [26]).

The devices have almost the same geometry. Their dimensions are large enough to have a number of quantized levels. In Fig. 8 each peak in the conductance corresponds to transfer of one electron, when an energy level enters into resonance with the electron states in the contacts. Though the conductance versus gate - voltage dependences are different, i.e. not reproducible, the peak spacing is the same for both devices. It is determined by the change in the gate voltage required to change the charging energy of the QDs by one electron. The Fig. 8 shows clearly that the electric current is modulated significantly by the gate voltage. Thus, for transistors with single - electron transport, strong control of very small electric current may be possible.

So far we have studied electronic nanoscale devices, i.e., a class of devices that exploits electrical properties of nanostructures and operates with electric input and output signals. another class is composed of optoelectronic devices, which are based on both electrical and optical properties of materials and work with optical and electric signals. In this paragraph we will analyze two very important classes of optoelectronic devices: light - emitting diodes and lasers (diodes as well as photodetectors. As will be shown below, the energy of the electric current flowing through these diodes is transformed into light energy. These optoelectronic devices have a huge number of applications and deserve consideration in details (see, also [22 - 31]).

Although stimulated emission [14] from the injection laser diode is very important (see, below), practically, sub - threshold operation of the diode - when only spontaneous light is emitted - is in many cases advantageous and has a number of applications. Diodes operating with spontaneous light emission are called light - emitting diodes [31]. The important characteristic of the light - emitting diode is the spectral distribution of emission The spectrum of emission is determined, primarily, by the electron/hole distributions. Thus, the ambient temperature T, defines both spectral maximum and the spectral width of emission. The peak value of the spectral distribution can be estimated as [3]

ℏω = E_g + ((k_BT)/2). (7)

The full width at half maximum of the distribution is Δω ≈ 2k_BT/ℏ and is independent of ω. In terms of the wavelength, λ, we obtain

Δλ = [λ_m²/(2πc)Δω

or

Δλ = 1.45λ²k_BT, (8)

where λ_{m} corresponds to the maximum of the spectral distribution, Δλ and λ_{m} are expressed in micrometers, and k_BT is expressed in eV. Fig. 41 in [22] shows the spectral density as a function of the wavelength for light - emitting diodes based on various materials. For these different materials, the spectral linewidth increase in proportion to λ², in accordance with Eq. (8). From indicated figure, one can see that light - emitting diodes cover a wide spectral region from the infrared - about 8 μm for InGaAsP alloys - to the near ultraviolet - 0.4 μm for GaN. Light - emitting diodes are, indeed very universal light sources [9].

Semiconductor lasers incorporating low - dimensional hetero-structures., QWs and QDs, are attracting considerable interest of their potential for improved performance over QW lasers (see, e.g. [31]). This prediction is based, in the single - particle picture, on the sharper density of states resulting from the confinement of the charge carriers in two or three directions. Among other advantages, the ideal QD and QWr lasers would exhibit higher and narrower gain spectrum, low threshold currents, better stability with temperature, lower diffusion of carriers to the device surfaces, and a narrower emission line than double heterostructure or QW lasers (see, also [22]). The observation of lasing from excitons in optically excited V - groove GaAs/AlGaAs QWr laser structures was detail describe in paper [27]. The observable emission is attributed to the recombinations of excitons associated with the lowest energy electron - and hole - subbbands of the QWr. Moreover these authors show that the emission energy remains nearly constant within the inhomogeneously broadened photoluminescence line of the QWrs for both continuous wave and pulsed optical excitation over a wide range of power densities. These results corroborate the important role played by electron - hole Coulomb correlations in the optical emission from quasi - 1D QWrs in the density regime of the Mott transition.

Optical emission of the QWr laser structure are displayed in Fig. 9 for different values of the optical power density below, at and above the threshold for lasing in the QWr.

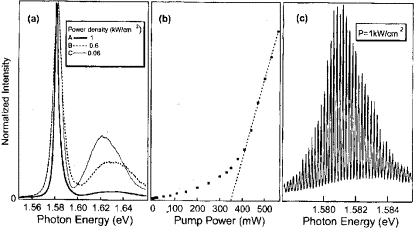
Fig. 9. (a) Photoluminescence spectra at 10 K of the QWr laser sample above, below and near the lasing threshold in TE - polarization. (b) Dependence on input excitation power of the PL output power;arrows indicate the excitation powers used for the optical spectra depicted in (a). (c) High resolution emission spectrum above the lasing threshold showing the Fabri - Perrot modes of the optical cavity (after [27]).

Upon increasing the pump power, these authors observe a nearly constant energy of the peak at 1.581 eV that corresponds to the optical transition e₁ - h₁ associated with the ground electron - hole - subband of the QWrs. A significant spectral narrowing is also found as the power density is increased and crosses the lasing threshold. This evidences the existence of amplified spontaneous emission within this inhomogeneously broadened PL line in this density regime. The observable emission intensity varies linearly at low excitation power over three orders of magnitude (from 0.1 to 100 mW) [27]). Above the lasing threshold (at 350 mW) the intensity variation is again linear (see, Fig.9^{b}), indicating that the modal gain is saturated. In Fig. 9^{c}, a high - resolution emission spectrum obtained above threshold features well - resolved Fabry - Perot modes that correspond to different longitudinal optical modes within the inhomogeneuous line of the QWr - PL (see also Fig. 10). Detailed investigations of PL and PLE spectra (see, Fig. 43 in [22]) of the QWr allowed the indicated authors to conclude that the lasing emission originates from the recombination of excitons as it is case for the QWr - peak of the cw - PL spectrum (details see [27]).

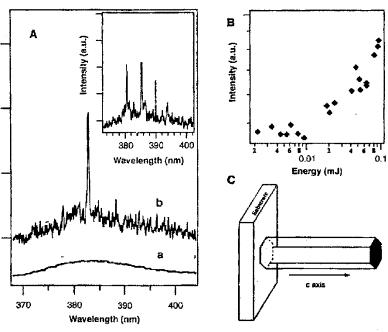
Fig. 10. (A) Emission spectra from nanowire arrays below (line a) and above (line b and inset) the lasing threshold. The pump power for these spectra are 20, 100 and 150 kW/cm², respectively. The spectra are offset for easy comparison. (B) Integrated emission intensity from nanowires as a function of optical pumping intensity. (C) Schematic illustration of a nanowire as a resonance cavity with two naturally faceted hexagonalend faces acting as reflecting mirror. Stimulated emission from the nanowires was collected in the direction along the nanowire's end - plane normal (the symmetric axis) with a monochromator combined with a Peltier - cooled charge - coupled device. The 226 - nm pump beam was focused to the nanowire array at an angle 10⁰ to the end - plane normal.All experiments were carried at room temperature (after [30]).

In QDs, as indicated above, carriers are confined in the three directions in a very small region of space, producing quantum effects in the electronic properties. As we can see from Fig. 3, the electronic joint density of states for QD shows sharp peaks corresponding to transitions between discrete energy levels of electrons and holes. Outside these levels the DOS vanishes. In many ways, the electronic structure of a QD resembles that a single atom. Lasers based on QDs could have properties similar to those of conventional ion gas lasers, with the advantage that the electronic structure of a QD can be engineered by changing the base material, size and shape. In the next we assume that the QDs are small enough so that the separation between the first two electron energy levels for both electrons and holes is much larger than the thermal energy kT. Then for an undoped system, injected electrons and holes will occupy only the lowest level. Therefore, all injected electrons will contribute to the lasing transitions from the E_1e to the E_1hh levels, reducing the threshold current with respect to other systems with lower confinement. The evolution of the threshold current density obtained along the years for various laser structures is shown in Fig.11.

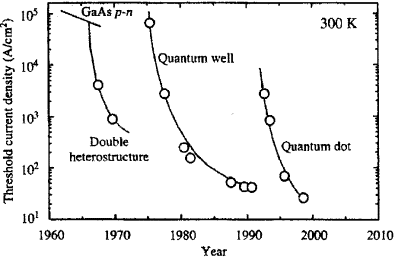
Fig.11. Evolution of threshold current density for lasers based on different confinement structures (after [29]).

The lowest threshold currents have already been reached for QD lasers [22]. As long as the thermal energy is lower than the separation between the fist and second levels, the emission band in an ideal QD laser is very sharp and does not depend on temperature (see, also [31]. Therefore, QD lasers should have a better stability with temperature without the need for cooling. We should add that QDs have the narrowest spectrum and the highest gain.

References.

1. K. Goser, P. Glösekötter, J. Dienstuhl, Nanoelectronics and Nanosystems (Berlin, Springer, 2004).

2. L. Esaki and R. Tsu, Supelattice and negative differential conductivity in semiconductors, IBM J. Res. and Develop. 14, 61 (1970).

3. M.J. Kelly, Low - dimensional Semiconductors (Oxford, Clarendon Press, 1995).

4. J.H. Davis, The Physics of Low - dimensional Semiconductors (Cambridge, Cambridge University Press, 1998).

5. P. Harrison, Qquantum Wells, Wires and Dots (New York, Wiley, 2001).

6. L. Esaki, in Molecular Beam Epitaxy and Heterostructures, ed. by L.L. Chang, K. Ploog (Dordrecht, Kluwer Academic, 1985).

7. V.G. Plekhanov, Applications of the Isotopic Effect in Solids (Berlin - Heidelberg, Springer, 2004).

8. V.G. Plekhanov, Isotope - based quantum information, ArXiv: quant - ph/ 0909.0820 (2009).

9. Single Semiconductor Quantum Dots, P. Michler (ed.) (Berlin - Heidelberg, Springer - Verlag, 2009).

10. M. Cardona and M.L.W. Thewalt, Isotope effect on optical spectra of semiconductor, Rev. Mod. Phys. 77, p. 1173 - 1224, October 2005.

11. V.F. Agekyan, A.M. Asnin, V.M. Kryukov et al., Isotope effect in germanium, Fiz. Tverd. Tela 31, (No 12) p. 101 -104 (1989) (in Russian).

12. M. Lax, E. Burstein, Infrared lattice absorption in ionic and homopolar crystals, Phys. Rev. 97 (No 1) p. 39 - 52 (1955).

13. H.D. Fuchs, P. Etchegoin, M. Cardona et al., Vibrational band modes in germanium: Isotopic disorder - induced Raman scattering, Phys. Rev. Lett 70, p. 1715 - 1718 (1993).

14. V.G. Plekhanov, Isotope Effect in Solid State Physics, in Semiconductors and Semimetals, Vol. 68 (R.K. Willardson and E. Weber (eds.)) (San Diego, CA, Academic Press, 2001).

15. H.Hanzawa, N. Umemura, Y. Nishida and H. Kanda, Disorder effect of nitrogen impurities, irradiation - induced defects and ¹³C composition on the Raman spectrum in syntethic I^{b} diamond, Phys. Rev. B54 (No 6) p. 3793 - 3799 (1996).

16. V.G. Plekhanov, Elementary excitations in isotope - mixed crystals, Phys. Rep. 410 (No 1 - 3) p. 1 - 235 (2005).

17. V.G. Plekhanov, Isotope effects in lattice dynamics, Physics - Uspekhi 46 (No 7) p. 689 - 715 (2003).

18. V.G. Plekhanov, Experimental evidence of strong phonon scattering in isotopical disordered systems: the case LiH_xD _1-x, Phys. Rev. B51 (No ) p. 8874 - 8878 (1995); ArXiv: cond - mat/ 0907.3817.

19. V.G. Plekhanov, Manifestation and Origin of the Isotope Effect, ArXiv:phys/ 0907.2024 (2009).

20. A.F. Kapustinsky, L.M. Shamovsky, K.S. Bayushkina, Thermochemistry of isotopes, Acta physicochem (USSR) 7 (No 6) p. 799 - 810 (1937).

21. F.I. Kreingol'd, K.F. Lider, M.B. Shabaeva, Influence of isotope substitution sulfur on the exciton spectrum in CdS crystal, Fiz. Tverd. Tela 26 (No 11) p. 3940 - 3941 (1984) (in Russian).

22. V.G. Plekhanov, Isotopetronics - new direction of nanoscience, ArXiv:phys/1007.5386 (2010).

23. L.M. Zhuravleva, V.G. Plekhanov, Nuclear technology in creation of low - dimensional isotope - mixed structures, Nanoindustry 4, (N 16) 32 - 35 (2009); Isotopical nanotechnology low - dimensional structures, Nano - and Microsystematic Technique N9 (122) 8 - 12 (2010) (in Russian).

24. M.H. Devoret and R.J. Schoelkopf, Amplifying quantum signals with the single - electron transistors, Nature 406, 1039 - 1046 (2000); Y. Ono, A. Fujiwara, K. Nishiguch, et al., Manipulation and detection of single electrons for future information processing, J. Appl. Phys. 97 (N 3) p. 031101 - 19 (2005).

25. Y. Ono and Y. Takahashi, Electron pump by a combined single - electron field - effect transistor, Appl. Phys. Lett. 82, 1221 1223 (2003).

26. M.A. Kastner, The single electron transistor, Rev. Mod. Phys. 64, 849 - 858 (1992).

27. L. Sirigu, D.Y. Oberli, L. Deriorgi et al., Excitonic lasing in semiconductor quantum wires, Phys. Rev. B61 (N 10) p. R10575 - 4 (2000).

28. L.A. Colderen and S.W. Corzine, Diode Lasers and Photonic Integrated Cicuits (New York, Wiley, 1995).

29. L.M. Zhuravleva and V.G. Plekhanov (in press).

30. M.H. Huang, S. Mao, H. Feick et al., Room - temperature ultraviolet nanowire nanolasers, Science 292, 1897 - 1899 (200).

31. V.M. Ustinov, A.E. Zukov, A.Yu. Egorov ans N.A. Maleen, Quantum Dot Lasers (Oxford, Oxford University Press, 2003).