Омарова Б.А.

Математическая модель для расчетов перемещений рельсовых плетей численными методами

Известно несколько математических моделей бесстыкового пути, применяемых для решения ряда задач[1,2].

Имитационная динамическая модель, принятая М.Ф.Вериго[1], предназначалась для расчета перемещений рельсов бесстыкового пути после начала выброса.

Для исследования динамического процесса потери устойчивости участка пути при движении по нему экипажа профессор М.Ф.Вериго использовал уравнение:

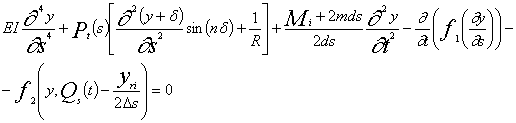
где - отнесенная к -ой колесной паре необресоренная масса при ее горизонтальных перемещениях, - рамная сила на той же колесной паре.

В Японии S.Miura и H.Yanagava [3] в 1992г. для рассмотрения количественных характеристик распределения продольных сил в рельсах провели теоретический анализ с использованием модели, представленной на рис.1.

Рис.1. Аналитическая модель бесстыкового пути, рассмотренная Miura

В этой модели учтены продольная и поперечная жесткость пути. Вертикальная жесткость не учтена и рассматривается только боковое смещение решетки. Для оценки уровня безопасности в отношении выброса пути Miura применил энергетический метод, основанный на изменении количества энергии при переходе рельса из прямолинейного в криволинейное состояние. В диапазоне низких температур рельсов ввиду небольших поперечных деформаций имеется только один минимум величины энергии, но при более высоких температурах из-за больших деформаций к нему добавляется еще несколько точек минимальных величин. Тогда выброс представляет собой переходный процесс от устойчивого состояния с небольшой деформацией в другое устойчивое состояние с большой деформацией. Чтобы такой переход произошел, необходима дополнительная энергия, величина которой представляет собой количественную характеристику устойчивости пути против выброса. В Японии считают, что бесстыковой путь применим и в крутых кривых, только там следует увеличить плечо балластной призмы, подсыпать дополнительный балласт в сочетании с использованием антивыбросных упоров.

Для оценки линейно-упругих перемещений рельсовых нитей нами предложена линейно-упругая модель бесстыкового пути. В моделях бесстыкового пути (рис.2) учитывается вертикальная, поперечная и продольная упругость пути и возможность поворота рельса в узле скрепления без отрыва от подкладки. Эта модель для прямых и кривых может учитывать прижатие рельса клеммой скрепления, отступления от норм содержания пути (просадки пути и углы по направлению), ослабления пути при производстве работ (количество освобожденных от балласта торцов шпал), многие другие факторы и заметно реагирует на изменение исходных данных в соответствующих областях значений.

Рис.2. Вариант конечно-элементной схемы бесстыкового пути: 1-рельс, 2‑вертикальная жесткость сжатия, 3-боковая жесткость, 4-связь рельса со шпалой, 5-продольная жесткость, 6-шпала, 7-вертикальная жесткость на отрыв пути от балласта, 8-жесткость относительно вращения

Рис.3. Представление узла промежуточного скрепления в конечно-элементной модели стрелочного перевода и примыкающих путей: 1-рельс, 2,3,4 – жесткость связи шпал или переводных брусьев с балластом, 5,6,7 – жесткость промежуточного скрепления, 8-шпалы или переводные брусья

Рис.4. Участок конечно-элементной модели стрелочного перевода

Для исследования эффектов воздействия температурных напряжений на элементы стрелочного перевода после сварки стыков внутри перевода и оценки усилий, действующих на перевод от примыкающих к стрелочному переводу бесстыковых плетей после сварки перевода с ними, была разработана конечно-элементная модель одиночного несимметричного стрелочного перевода типа Р65 марки 1/11 на железобетонных брусьях (например, проекта 2750). Геометрия и конечно-элементная сетка модели полностью повторяют реальную геометрию существующего перевода. В модели представлен сам стрелочный перевод и участки примыкающих путей. Модель состоит из более чем 8 тысяч узлов, 11 тысяч конечных элементов и описывается более чем 30 тысячами уравнений. Она адекватно описывает физические свойства элементов пути.

В предложенной модели рельсы и железобетонные брусья представлены в виде балок (Beam3D) с несимметричным сечением и соответствующими геометрическими характеристиками и свойствами материалов.

Взаимодействие шпал и брусьев стрелочного перевода с балластной призмой моделируется в виде системы упругих элементов, которая имеет суммарную приведенную упругость, характеризующуюся 6 величинами – 3 упругостями относительно сдвигов (трансляций) и 3 упругостями относительно вращений. Брусья имеют различную длину вдоль стрелочного перевода, соответствующим образом задаются и параметры упругих элементов сопротивления сдвигу вбок, которые приняты пропорциональными длине бруса. Так как в современных конструкциях стрелочных переводов длина брусьев меняется вдоль перевода "ступеньками", то и параметры упругих элементов задаются таким же образом. В использованной для массовых расчетов модели взаимодействие брусьев и шпал с балластом было представлено в виде отдельных комплектов из 5 упругих элементов (Spring), для каждого из которых задавались упругость относительно осевых деформаций и вращений .

Различные типы промежуточных рельсовых скреплений, которые применяются в составе стрелочного перевода, представлены в модели в виде системы упругих элементов, создающих между рельсом (по уровню его головки) и брусьями упругость, характеризующуюся 6 величинами. В использованной для массовых расчетов модели на каждый узел промежуточного скрепления была применена система из 4 абсолютно жестких элементов (RBar) и 5 упругих элементов (Spring) с соответствующими упругостями относительно сдвигов (трансляций) и вращений. Свойства упругих элементов, представляющих промежуточные скрепления, задаются вдоль стрелочного перевода и примыкающих путей в соответствии с типами скреплений, применяемыми на стрелочном переводе и примыкающих путях.

Литература.

1	Вериго М.Ф. Динамические модели устойчивости бесстыкового пути // Железные дороги мира, 1994, №10, стр.3-9.
2	Вериго М.Ф., Коган А.Я. Взаимодействие пути и подвижного состава. Москва, Транспорт, 1986. 559с.
3	Miura S., Vanagava H. Japanese Railway Engineering, №120, 1992. р.21-24.