Панченко Р.М.

Національний технічний університет України «КПІ»

АКУСТИЧНЕ ВИПРОМІНЮВАННЯ ТА ОСОБЛИВОСТІ ПОБУДОВИ РОЗРАХУНКОВИХ МОДЕЛЕЙ ЙОГО ДІЇ

Аналізуючи вплив акустичного навантаження на елементи апаратури та обладнання, потрібно передусім розглядати окремо вплив низького (до 130 дБ) та високого (понад 150 дБ) рівнів звукового тиску. Якщо вплив низьких рівнів досить ґрунтовно вивчений і систематизований, то дію акустичного випромінювання високої інтенсивності вивчено і висвітлено в літературі значно менше. Особливо важливою постає проблема впливу проникного акустичного випромінювання на електронну та навігаційну апаратуру рухомих об’єктів.

Відомо, що зі збільшенням потужності двигунів літальних апаратів зростає створюваний ними шум. Причому близько 0,7 % потужності двигунів витрачається на акустичне випромінювання, загальний рівень якого, наприклад, біля реактивного струменя може досягати 180 дБ і більше. Зокрема, це стосується стартів носіїв із малих об’ємів або з пускових установок мобільного базування. Звичайно, звуковий тиск такого рівня чинить неабиякий вплив на елементи радіоелектронного та навігаційного обладнання. Шум реактивного струменя, маючи широкий спектр частот (40…10 000 Гц) та випадковий характер зміни звукового тиску, зумовлює в конструкції безліч форм коливань, у тому числі й резонансних. Інколи акустичний вплив призводить до втоми матеріалу та появи незворотних деформацій або тріщин.

Виникнення хвильових процесів в елементах апаратури породжує зміну режиму їх паспортного функціонування, а в сукупності – погіршує їхні технічні характеристики.

Виявлено, що акустичне випромінювання від шуму реактивного струменя досягає найбільшого значення під час старту з поверхні землі. З підвищенням швидкості польоту його рівень знижується, але зростають прояви інших причин випромінювання, наприклад, від пульсацій тиску в турбулентному примежовому шарі. На літаках з турбогвинтовими двигунами змінний тиск утворюється на панелі фюзеляжу, переважно в зоні обертання гвинта.

Особливістю випромінювання звуку аеродинамічним потоком є наявність сферичних звукових хвиль і гостронапрямлених інтенсивних хвиль Маха, які є основним джерелом шуму. Середній квадрат акустичного тиску, наприклад, високошвидкісних ракет, можна обчислити за формулою

де – безрозмірний коефіцієнт рівня турбулентності; – довжина звукової хвилі; – густина середовища; – швидкість струменя витікання; – число Маха; – кут між напрямками руху вихорів і випромінювання.

За невеликих швидкостей це рівняння узагальнює закон «восьмого ступеня» Лайтхілла. Найбільший інтерес становить випадок, коли , що відповідає максимуму шуму, який випромінюється струменем ракетного двигуна.

Шум ракетних двигунів поширюється як через середовище, так і через елементи конструкції корпусу рухомого об’єкта (аналогічно звуковому містку) внаслідок виникнення в матеріалі горизонтально й вертикально поляризованих хвиль, а також їх суперпозиції (еліптична поляризація). Крім того, утворюються хвилі Стоунлі, які локалізуються поблизу межі поверхні корпусу і є наслідком виникнення явищ резонансного типу.

Дослідження показали, що частина звукової енергії поглинається ребрами шпангоутів, а частина – погонною масою оболонки носія. Причому повний опір, наприклад, для космічних апаратів, визначається сумою внутрішнього механічного опору конструкції та опору випромінюванню у вигляді енергії з конструкції в середовище.

Будь-які порушення стаціонарності стану суцільної рідини, твердого чи газоподібного середовища в будь-якій точці простору призводять до появи поширюваних від цієї точки збурень, які називаються хвилями.

У твердому середовищі можуть поширюватися поздовжні хвилі, в яких частки коливаються вздовж напрямку поширення, та поперечні хвилі, в яких частки коливаються в площинах, перпендикулярних до напрямку поширення. З рівнянь руху твердого середовища (рівнянь теорії пружності) доведено, що будь-який хвильовий рух твердого тіла складається з суми поздовжніх і поперечних хвиль.

У рідині й газі поширюються лише поздовжні хвилі і будь-який хвильовий рух у цих середовищах складений лише з поздовжніх хвиль, що поширюються в різних напрямках. У діапазоні частот від 16 Гц до 20 кГц, в якому коливання сприймаються вухом людини як звук (звуковий діапазон) хвилі називаються звуковими. Коливання з частотами нижче 16 Гц є інфразвуковими, а понад 20 кГц – ультразвуковими.

Зміна стану середовища, в якому поширюються звукові хвилі, характеризується тиском (в Па) – перевищенням над тиском у незбуреному середовищі, густиною середовища (в Н·м^-3) та вектором швидкості коливань часток середовища (в м·с^-1). Область середовища, в якій поширюються звукові хвилі, називається звуковим полем.

Поширення хвиль у рідині й газі підпорядковується нелінійним рівнянням аерогідродинаміки – рівнянням руху, нерозривності та стану, точне розв’язання яких становить значні математичні труднощі. Тому в акустиці для опису звукового поля використовують наближені рівняння, які будуються після лінеаризації рівнянь аерогідродинаміки, що можливе для більшості реальних звукових процесів. Якщо частота звуку не досить велика і поширення хвиль (звуку) розглядається на невеликій відстані, то, як правило, можна нехтувати впливом в’язкості й теплопровідності, а акустичні рівняння поля в нерухомому однорідному середовищі записати у вигляді

(1)

де перше рівняння є рівнянням руху в проекції на вісь (рівняння Ейлера), друге – рівнянням нерозривності, третє – рівнянням стану; проекції швидкості часток середовища на осі прямокутної (декартової) системи координат; проекція на вісь зовнішньої сили, що прикладається до одиничного об’єму середовища; продуктивність джерел – додаткова маса, яка надходить за одиницю часу в одиничний об’єм; зміна густини середовища; швидкість звуку; об’ємний модуль пружності (всебічного стиснення).

Рівняння Ейлера в проекціях на осі та дістають заміною відповідних індексів у наведених рівняннях.

Розв’яжемо систему рівнянь (1.103) відносно звукового тиску:

За відсутності джерел звуку в середовищі, тобто при і , права частина цього рівняння перетворюється на нуль, і поширення звуку буде підпорядковане хвильовому рівнянню

(2)

Рівняння (2) лінійне, тому та , а також їх сума будуть його розв’язками. Це означає, що хвилі мають поширюватися незалежно одна від одної.

У більшості випадків, на практиці, звукові поля є безвихровими, потенціальними, тобто існує потенціал швидкостей (функція координат і часу), пов’язаний зі швидкістю часток середовища співвідношеннями

Потенціал швидкостей та густина середовища також задовольняють хвильове рівняння в тій частині простору, де немає джерел звуку. Потенціал швидкостей є зручним поняттям у розв’язанні багатьох задач акустики, оскільки замість трьох невідомих функцій потребує лише одну – .

Звуковий тиск пов’язаний з потенціалом швидкостей співвідношенням

.

У сферичній системі координат (рис. 1.) хвильове рівняння (2) в області, вільній від джерел звуку, має вигляд

(3)

Використовуючи променеву теорію, проходження звуку крізь плоску перешкоду можна пояснити механічною моделлю (рис. 2).

Найпростішими є плоскі звукові хвилі (рис. 3), які залежать лише від однієї декартової координати, наприклад, . Джерелом плоскої хвилі можна вважати пульсуючу в напрямку нормалі нескінченну за розміром площину.

Будь-яку плоску хвилю можна зобразити розв’язком хвильового рівняння:

де і – довільні функції однієї змінної.

Величина зображує плоску хвилю, яка поширюється в додатному напрямку осі зі швидкістю (пряма хвиля), а – плоску хвилю у від’ємному напрямку осі з тією самою швидкістю (зворотна хвиля). Швидкість звуку у повітрі при температурі 20ºС та атмосферному тиску 10⁵ Па (нормальні атмосферні умови) дорівнює 344 м·с^-1.

Швидкість руху часток середовища в прямій хвилі пов’язана зі звуковим тиском співвідношенням

а у зворотній –

Із цих формул випливає, що в точках з додатним тиском частки рухаються в напрямку поширення хвилі, а в точках з від’ємним тиском – у протилежному напрямку. Відношення звукового тиску до швидкості часток у плоскій біжучій хвилі

однакове в усіх точках півпростору. Воно називається хвильовим опором середовища. Для повітря за нормальних атмосферних умов Н·с·м^–3.

Іншими, досить поширеними видами хвиль є циліндричні та сферичні. Циліндричні розглядаються як наслідок осьових пульсацій поверхні нескінченного за довжиною циліндра в напрямку твірної з нульовою кривизною (у напрямку осі , рис. 4), а сферичні – як наслідок пульсацій сфери в радіальному напрямку (рис. 5).

Для опису динаміки циліндричних оболонок доцільно використовувати циліндричні координати (рис. 6), а для сферичних поверхонь – сферичні (рис. 1.48). Тут – азимут; – радіус; – апліката; – полярний радіус; – полюсний кут.

До найпростіших належать також сферично-симетричні хвилі, які залежать, крім часу, лише від відстані до центра. Звуковий тиск у будь-якій сферично-симетричній хвилі задовольняє рівняння (3) і може бути наведений у вигляді

Перший доданок описує розбіжну хвилю, другий – збіжну. На відміну від плоских, звуковий тиск у сферичних хвилях зменшується зі збільшенням відстані від центра.

Перенесення енергії звуковою хвилею характеризується вектором миттєвої інтенсивності звуку (густини потоку звукової потужності), Вт·м^–2,

Його середнє за певний час значення обчислюється за виразом

і називається вектором інтенсивності звуку. Проекція вектора на нормаль до будь-якої площини дорівнює миттєвому (середньому за час) значенню густини потоку звукової потужності крізь одиницю площі:

.

В акустичних розрахунках часто розглядають проекцію вектора інтенсивності звуку на визначений напрямок , опускаючи індекс і позначаючи його .

У разі гармонічних звукових хвиль швидкість часток можна розділити на дві складові:

Перша складова синфазна зі звуковим тиском , а друга – зсунута за фазою на . Величину називають вектором активної інтенсивності, а вектором реактивної інтенсивності. Середнє за час значення першого вектора дорівнює , а другого – нулю.

Другою енергетичною характеристикою звукового поля є густина звукової енергії (в Дж·м^–3), яка дорівнює усередненій у часі сумі потенціальної та кінетичної енергій хвилі в обраній точці простору.

Інтенсивність звуку і густина звукової енергії тісно пов’язані з величинами, які визначають вплив звуку на людину.

Джерело звуку (випромінювач) характеризується звуковою акустичною потужністю, частотним спектром випромінювання та характеристикою напрямленості.

Звуковою потужністю (у Вт) джерела звуку є загальна звукова енергія, яка випромінюється ним за одиницю часу. Вона визначається потоком інтенсивності звуку крізь замкнену поверхню площею , яка оточує джерело звуку:

де – зовнішня нормаль до поверхні.

Більшість реальних джерел випромінюють звук неоднаково в різних напрямках. Нерівномірність випромінювання звуку джерелом характеризується фактором напрямленості , який визначається відношенням інтенсивності звуку, що створюється джерелом у вільному полі в заданій точці сфери, в центрі якої він перебуває, до середньої інтенсивності звуку на поверхні сфери:

де – радіус сфери.

Величина нормована й підпорядкована співвідношенню

де – елемент тілесного кута , в який випромінюється звук.

Напрямленість випромінювання характеризується також відношенням інтенсивності звуку (чи звукового тиску) в заданій точці простору до інтенсивності (чи звукового тиску) на осі випромінювача на тій самій відстані від нього.

На практиці користуються такими рівняннями:

інтенсивності звуку (в дБ)

звукового тиску (в дБ)

швидкості часток (в м/с)

де Вт·м^–2; Па; м·с^–1 – початкові інтенсивність звуку, середньоквадратичний звуковий тиск і швидкість часток. За нормальних атмосферних умов для плоскої хвилі .

Рівень звукової потужності (в дБ) джерела шуму визначається співвідношенням

де Вт – початкова потужність, яка дорівнює потужності звукової хвилі інтенсивністю , що переноситься крізь одиничну поверхню площею м².

Гармонічні коливання та хвилі займають особливе становище в акустиці. Пояснюється це тим, що в більшості випадків детерміновані чи випадкові коливання частки в кожній точці середовища можуть бути зображені у вигляді суми чи інтеграла гармонічних коливань різних частот. Тому замість вивчення поширення хвиль з будь-якою залежністю від часу можна вивчати лише гармонічні хвилі, закони випромінювання, поширення, відбивання та поглинання яких простіші, ніж у хвиль з іншою залежністю в часі.

Звуковий тиск у гармонічній хвилі:

(4)

де кутова частота коливань, с^–1; і – відповідно амплітуда й початкова фаза коливань, які залежать лише від координат.

У цьому разі звук називається чистим тоном і його частота

а фаза коливань

Аналогічний вигляд має швидкість переміщення точок середовища.

Гармонічні хвилі підпорядковані рівнянню Гельмгольца

де – хвильове число, м^–1.

Інтенсивність звуку в гармонічній хвилі

де і – амплітуди звукового тиску та швидкості часток середовища в певній точці; – зсув фаз між ними.

В акустичних розрахунках вираз (4) використовують рідко. Частіше застосовують комплексну форму

де – комплексна амплітуда, яка залежить від місцезнаходження точки; – уявна одиниця.

Плоска гармонічна хвиля, що переміщується в додатному напрямку осі , у комплексній формі має вигляд

де – амплітуда плоскої хвилі.

З цієї формули випливає, що плоска гармонічна хвиля періодична не лише в часі, але й у просторі в напрямку координати . Період зміни хвилі в просторі, зокрема відстань між двома максимумами (чи мінімумами) звукового тиску

,

називається довжиною хвилі. У звуковому діапазоні частот довжина хвилі в повітрі становить від декількох десятків метрів до декількох сантиметрів.

Для кожної точки середовища середній у часі квадрат звукового тиску в плоскій хвилі

інтенсивність звуку в напрямку поширення плоскої хвилі

густина звукової енергії

Швидкість перенесення звукової енергії плоскої хвилі дорівнює швидкості звуку.

Для опису гармонічних процесів у комплексній формі в акустиці широко використовується поняття імпедансу. Він визначається відношенням комплексного тиску до комплексної швидкості

і не залежить від часу. За допомогою імпедансів характеризують випромінювальні властивості джерел звуку, звукоізоляційні властивості перешкод, властивості звукопоглинальних поверхонь тощо. У більшості випадків імпеданс – частотно залежна комплексна величина, яка може бути також функцією місця його визначення.

Інтенсивність звуку в певній точці простору можна обчислити за допомогою імпедансу для цієї точки, використовуючи формулу

Якщо плоска хвиля падає на межу розділу двох середовищ з хвильовими числами та ( і – швидкості звуку в першому й другому середовищах), то її тиск і потенціал швидкості можна подати залежностями

де – амплітуда тиску у звуковій хвилі; – хвильовий вектор; – одиничний вектор у напрямку поширення хвилі; – радіус-вектор точки, потенціал швидкості якої визначається.

У цьому разі скалярний добуток для падаючої, відбитої та прохідної хвиль відповідно описується виразами

Тут використано закон відбиття, згідно з яким кут падіння хвилі дорівнює куту її відбиття. Кут заломлення пов’язаний з кутом падіння співвідношенням

яке відображає закон Снелліуса. Отже, для падаючої хвилі маємо:

Під час розв’язання багатьох прикладних задач акустичний тиск зручно розглядати як сукупність симетричної та антисиметричної складових (рис. 8):

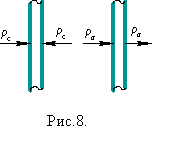де – відповідно амплітуди тиску в падаючій, відбитій та прохідній хвилях.

Зрозуміло, що симетрична складова стискує або розтягує пластину в напрямку товщини, а антисиметрична – розгойдує її (вправо, вліво) аналогічно маятнику.