Карачун В.В., Мельник В.М., Лозовик Т.М., Заброда А.О., Саверченко В.Г.

Національний технічний університет України «КПІ»

ЦИРКУЛЯЦІЯ РУХОМОГО ОБ‘ЄКТУ В ПРОСТОРІ. СИНТЕЗ РУХІВ

Припустимо, що рухомий апарат і зв’язана з ним система координат виконує переносний рух в абсолютній системі координат . В свою чергу, із цього апарату стартує об’єкт , з яким пов’язана система координат . Його рух в системі координат являється відносним, в системі координат – абсолютним.

Задання положення стартуючого об’єкту в просторі. Положення координатної системи визначається трьома координатами полюса , , та дев’ятьма напрямними косинусами між осями , , та , , (рис. 1).

Аналогічно, положення стартуючого об’єкту в системі координат задається трьома „відносними” координатами полюса – , , , та дев’ятьма напрямними косинусами між осями , , та , , . Природно, що абсолютному його рухові будуть відповідати три координати полюса , , і дев’ять напрямних косинусів між осями , , та , , .

В табл. 1 наведені основні кінематичні характеристики.

Таблиця 1

Характер руху

Переносний

Відносний

Абсолютний

Координати полюса

, ,

, ,

, ,

Напрямні

косинуси

В прикладних задачах часто виникає необхідність визначення положення об’єкта в одному із рухів – в абсолютному, переносному чи відносному за умови, що інших два відомі.

Так, якщо треба виявити положення об’єкта в абсолютному русі, при заданих відносному і переносному, хід логічних міркувань наступний.

Координати полюса стартуючого об’єкта в абсолютному русі обчислюються з рис. 1:

(1)

.

Абсолютні напрямні косинуси можна виявити через переносні та відносні за допомогою відомої формули аналітичної геометрії для косинуса кута між двома просторовими прямими:

.

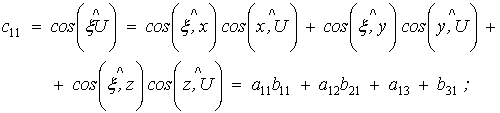
Має місце чергування подвійних індексів:

(2)

Аналогічно визначається положення стартуючого об’єкта у відносному русі (відносно носія), якщо, навпаки, відомі абсолютний і переносний рухи:

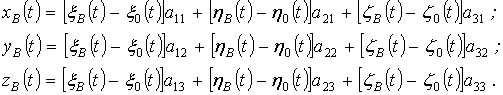(3)

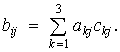
Для визначення координат полюса О рухомого апарату (носія) в переносному русі можуть бути враховані співвідношення (1), а напрямні косинуси обчисляться за формулою:

(4)

Синтез рухів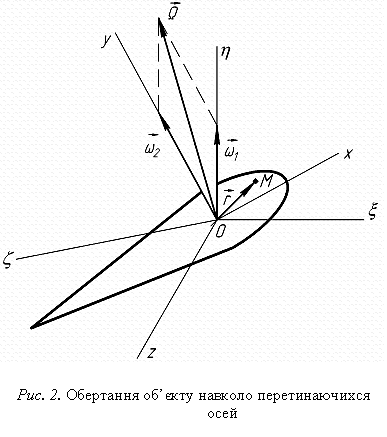. Обертання об’єкту навколо перетинаючихся осей.

Припустимо, що технічне завдання рухомого об’єкту передбачає в якийсь проміжок часу здійснення ним двох обертальних рухів. Навколо осі з кутовою швидкістю і навколо осі з кутовою швидкістю (рис. 2). Для спрощення вважаємо полюс нерухомим.

Відносним є рух навколо осі , переносним – навколо осі . Шукаємо абсолютну кутову швидкість . Оберемо на об’єкті довільну точку , положення якої задане вектором

, (5)

де , , – орти рухомої системи.

Абсолютна швидкість т. дорівнює геометричній сумі відносної швидкості та переносної , тобто

. (6)

З наведеної формули походить, що сукупність двох обертальних рухів навколо осей, що перетинаються еквівалентна одному обертальному руху навколо миттєвої осі з кутовою швидкістю, яка дорівнює геометричній сумі складових. Тобто,

.

Сукупність n обертальних рухів еквівалентна одному, з кутовою швидкістю

.

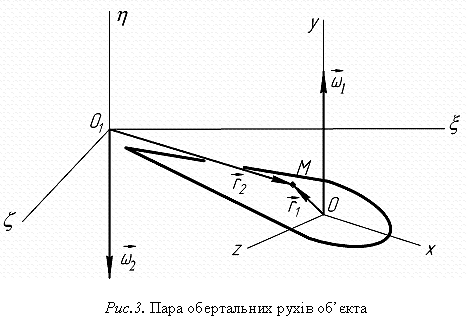
Пара обертань. Припустимо, що об’єкт обертається навколо паралельних осей та з рівними за величиною і протилежними за знаком кутовими швидкостями відповідно та (рис. 3). Причому

.

Обчислимо абсолютну швидкість довільної точки об’єкту:

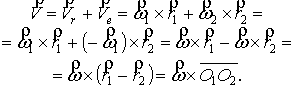
Тобто абсолютна швидкість не залежить від місцезнаходження точки, а це буває тільки за миттєво поступального руху.

Обертання навколо паралельних осей. Нехай об’єкт обертається у відносному русі навколо осі з кутовою швидкістю , а у переносному русі навколо осі з кутовою швидкістю (рис. 4), причому

; .

Абсолютна швидкість т. обчислюється за формулою:

Вираз в круглих дужках обертається на нуль, бо відносна швидкість дорівнює за величиною і протилежна за напрямом переносній швидкості . Точка ділить пряму у співвідношенні

.

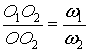Таким чином два обертальні рухи об’єкта еквівалентні одному обертальному рухові навколо миттєвої осі, що проходить через т. , з кутовою швидкістю .