УДК 519.6

Беляева В.В., Гунько Е. Ю., Машихина П. Б., Чорная А. Ю.

Днепропетровский национальный университет

математическое моделирование переноса токсичных веществ в ПОМЕЩЕНИЯХ

В настоящее время особую актуальность приобретает вопрос проектирования систем аварийной вентиляции, задачей которой является максимально быстрое снижение концентрации токсичного вещества в производственном помещении после аварии. При проектировании систем аварийной вентиляции используются положения СНиПа [5], согласно которым назначается величина аварийного воздухообмена в производственном помещении. Величина этого воздухообмена получена, как правило, на базе решения задач вентиляции помещения с помощью балансовых соотношений или на основе аналитического решения одномерного уравнения конвективно-диффузионного переноса примеси. [5] Эти расчётные методы не позволяют учитывать такие факторы:

· форма помещения;

· расположение в помещении оборудования;

· место аварийного выброса токсичного вещества;

· характер выброса (залповый, полунепрерывный и т.д.);

· положение приточных и вытяжных отверстий.

В настоящей работе рассматривается разработка специализированного метода расчёта процесса вентиляции помещений при аварийном выбросе токсичных веществ, который позволил бы в процессе расчета учесть перечисленные факторы. Предложенный метод расчёта базируется на создании численной модели процесса миграции примеси в помещении на базе трёхмерного уравнения конвективно–диффузионного переноса загрязнителя в воздушной среде. Поле скорости воздушного потока в помещении рассчитывается на базе модели течения невязкой несжимаемой жидкости.

Математическая модель. Для моделирования процесса переноса загрязняющего вещества в помещении будем использовать трехмерное уравнение миграции примеси [2, 3]

(1)

где С - концентрация загрязняющего вещества в помещении; u, v, w – компоненты вектора скорости воздушной среды; - скорость оседания примеси; μ= (μ_х, μ_y, μ_z) – коэффициент турбулентной диффузии; Q – интенсивность выброса токсичного вещества в помещении; - дельта-функция Дирака; r_i= (x_i,, y_i, ,z_i) – координаты источника выброса.

Для расчета поля скорости воздушного потока в помещении, индуцированного работой вентиляции делается допущение, что движение воздушной среды в помещении – потенциальное, тогда компоненты скорости воздушной среды определяются соотношениями

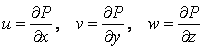, где - потенциал.

Уравнение для определения потенциала имеет вид

. (2)

Постановка краевых условий для уравнения (1) рассмотрена в работе [3]. Для уравнения (2) ставятся следующие граничные условия:

· на твердых стенках , где - единичный вектор внешней нормали;

· на входной границе (границы втекания воздушного потока в помещение) , где - известное значение скорости;

на выходной границе (условия Дирихле).

Метод решения. Численное интегрирование уравнений модели осуществляется на прямоугольной разностной сетке. Величина потенциала скорости определяется в центре разностных ячеек, а компоненты вектора скорости – на гранях разностных ячеек. Для численного интегрирования уравнения (2) используется идея установления решения по времени с последующим применением попеременно-треугольного метода А. А.Самарского [4], а также неявная схема условной аппроксимации.

Для численного интегрирования уравнения (1) применяется неявная попеременно – треугольная разностная схема [2].

На базе построенной математической модели разработан пакет прикладных программ, который был применен для численного моделирования процессов загрязнения воздушной среды при аварийной утечке аммиака, а также для моделирования процесса дезинфекции помещения от бактериологического загрязнителя (при решении этой задачи моделировался также процесс проникновения специально газа в щели).

Список литературы

1. Аварии и катастрофы. Предупреждение и ликвидация последствий. Учебное пособие в 5-ти книгах (Под редакцией В. А. Котляревского и А. В. Забегаева). М.: Из-во АСВ, 2001-200с.

2. Згуровский М. З., Скопецкий В. В., Хрущ В. К., Беляев Н. Н. Численное моделирование распространения загрязнения в окружающей среде. -Киев: Наукова думка.-1997.-368с.

3. Марчук Г. И. Математическое моделирование в проблеме окружающей среды. - М.: Наука. - 1982. - 320с.

4. Самарский А. А. Теория разностных схем / 2-е изд., испр. - М.: Наука. - 1983. - 616с.

5. Эльтерман В. М. Вентиляция химических производств / 3-е изд., перераб. - М.: Химия. - 1980. - 288с.