Математика/1                                                                                                 Диференціальні та

                                                                                            інтегральні рівняння

Шевчук Н. М.

Чернівецький національний університет імені Юрія Федьковича

Про одне узагальнення операцій диференціювання у просторах типу                                                                                  

 

У теорії аналітичних у крузі функцій досліджуються лінійні неперервні відображення у вигляді диференціальних або інтегральних операторів скінченного або нескінченного порядків, операторів узагальненого диференціювання або інтегрування, операторів Пом’є та обернених до них операторів.

Важливий клас операторів узагальненого диференціювання та інтегрування утворюють оператори Гельфонда-Леонтьєва, які позначаються символами Dn(F, ×),  n Î N. Якщо F(z) = ez, n = 1, то D1(ez, ×) збігається із звичайним оператором диференціювання, а -із оператором інтегрування. При дослідженні проблеми про класи єдиності та класи коректності задачі Коші для рівнянь з частинними похідними зі сталими (або залежними лише від часу) коефіцієнтами використовуються простори типу S, введені І.М.Гельфандом і Г.Є.Шиловим [1], та простори типу W, введені Б.Л.Гуревичем. Простори типу  складаються з нескінченно диференційованих на дійсній вісі функцій, поведінка яких та їхніх похідних на  характеризується величинами  , де подвійна послідовність  задовольняє певні умови (особливо повно досліджено випадок    ).

Простори типу W є узагальненнями просторів типу S внаслідок заміни степеневих довільними опуклими, що дозволяє точніше охарактеризувати особливості зростання або спадання функцій на нескінченності.

Простори W. Розглянемо функцію w: [0; +¥) ® [0; +¥), яка є неперервною і зростаючою, причому w(0) = 0,  = +¥. Для x ³ 0 покладемо W(x) = . Функція W володіє такими властивостями:

1)                W є диференційовною, зростаючою на  [0; +¥) функцією, причому W(0)=0,  =  +¥;   2) W – опукла функція, тобто: [0; +¥); W(x1) + W(x2) £ W(x1 + x2);

         Довизначимо функцію W на (–¥; 0] парним чином. Оскільки похідна функції W (функція w) при  x ® +¥ необмежено зростає, то сама функція W при |x| ® ¥ зростає швидше за довільну лінійну функцію. Поруч розглянемо функцію m : [0; +¥) ® [0; +¥) і покладемо M(x) = ,  M(–x) = M(x). Функція M за своїми властивостями аналогічна функції W. За допомогою функцій M і  Б.Л.Гуревич ввів серію просторів, названих ним просторами типу W.  Простір  будується за двома функціями W та M і визначається як сукупність цілих функцій j : C ® C, для яких

$c > 0  $a > 0 $b > 0 " z = x + iy Î C : |j(z)| £ c exp{–M(ax) + W(by)}.

 також можна подати як об’єднання зліченно-нормованих просторів , де  складається з тих функцій j Î , для яких правильні нерівності

|j(x + iy)| £ c exp{–M(x) + W(y)}, z = x + iy Î C,

де  – довільна додатна стала, менша за a,  –  довільна стала, більша за b.

  Якщо для  покласти

          

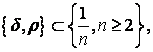
то з цими нормами  стає повним досконалим зліченно-нормованим простором. Збіжність в  еквівалентна збіжності: послідовність

 {j n, n ³ 1} Ì  збігається в  до нуля коли вона: 1) рівномірно збігається до нуля на кожній обмеженій замкненій множині Q Ì C,

 2) і із одними і тими ж сталими  a, b, c > 0, не залежними від .

Оператори узагальненого диференціювання Гельфонда-Леонтьєва у просторах типу W. Властивості операторів Гельфонда-Леонтьєва досліджували багато математиків у просторі  аналітичних у крузі радіуса , 0 < R £ ¥, функцій з топологією компактної збіжності. Оператори Гельфонда – Леонтьєва складають важливий клас операторів узагальненого диференціювання.

Оператором Гельфонда-Леонтьєва називається оператор, побудований за допомогою послідовності {ak, k Î Z+}, для якої

                     = (der)1/r, 0 <  d, r < +¥,                         (1)

тобто ak, k Î , – коефіцієнти Тейлора деякої спеціальної цілої функції F порядку r і типу d. Такий оператор позначається символом Dn(F, ×), n Î N, і визначається так. Нехай j(z) =  – довільна функція з простору AR; тоді

                             Dn(F, j)(z) := .                                  (2)

Внаслідок умови (1) існує границя  = 1, тому ряд (2) збігається в крузі |z| < R, тобто функція Dn(F, j) регулярна в тому ж крузі, що і функція j. Відзначимо відомі властивості оператора Dn(F, ×):

1) Dn(F, j 1 + j 2) = Dn(F, j 1) + Dn(F, j 2);

2) якщо c – стала, то Dn(F, cj ) = c Dn(F, j );

3) D m(F, Dn(F, j )) = D m + n(F, j ); 4) Dn(F, F(lz)) = l nF(lz), l – стала;

5) якщо F(z) = e z, то Dn(ez, j) = j.

 Ці властивості показують, що вираз  справді можна розуміти як узагальнену похідну порядку від функції , яка породжена функцією  (замість функції ). Оператор  звичайного диференціювання в  є частковим випадком оператора , який будується за послідовністю  , .

Теорема 1. Оператор узагальненого диференціювання Гельфонда-Леонтьєва Dn(F, ×) визначений коректно на W для довільного фіксованого n Î N і неперервно відображає цей  простір у (функція задовольняє умови нетривіальності з [2] ).

Оператори Гельфонда-Леонтьєва нескінченного порядку. Нехай g(z) =  – деяка ціла функція. Говоритимемо, що в просторі W задано оператор узагальненого диференціювання  Гельфонда-Леонтьєва нескінченного порядку g(D(F,×))º, якщо для довільної основної функції j ÎW ряд g(D(F,j))(z): =  зображає деяку основну функцію з простору .  

Теорема 2. Якщо ціла функція g задовольняє умову

"e > 0  $ce > 0 " z = x + iy Î C : |g(z)| £ ce ,

то в просторі W визначений оператор Ag:= g(D(F, ×)); при цьому Ag відображає W неперервно в .

1. Гельфанд И.М., Шилов Г.Е. Пространства основных и обобщенных  функций. – М.: Физматгиз, 1958. – 307с.

2. Готинчан Т.І. Про нетривіальність та вкладення просторів типу// Науковий вісник Чернівецького університету: Зб. наук. пр. Вип.160. математика. – Чернівці: Рута, 2003. – С. 39 – 44.