История/3. История науки и техники

Захарова О.А.,Соболев М.Е.

Павлодарский государственный университет им. С.Торайгырова, Казахстан

История изучения некоторых кривых высших порядков

При обучении аналитической геометрии на плоскости изучаются чаще кривые второго порядка, такие как эллипс, гипербола и парабола. Все эти кривые связаны с теорией конических сечений, открытой в древности Аполлонием, но задолго до того, как возникла общая теория конических сечений, был изучен ряд отдельных кривых для решения античных задач. [1]. Такие кривые открывались, изучались многими выдающимися учеными и в дальнейшем. Приведем в данной статье примеры некоторых специальных кривых и историю их изучения.

Первая из рассматриваемых кривых будет Архимедова спираль, которая была открыта Архимедом в третьем веке до нашей эры, когда он экспериментировал с компасом. Ученый тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние. Спираль Архимеда представляет собой одну из трансцендентных кривых и является квадратиссой. [2] В семнадцатом веке она привлекала внимание ученых изучением ее спрямления, отсутствующего в работах Архимеда. Так, Кавальери, Ферма, Паскаль доказали, что спрямление данной спирали может быть приведено к спрямлению параболы. Спираль Архимеда – плоская кривая, задаваемая уравнением r=aφ, где a– некоторое фиксированное число. Геометрическим свойством, характеризующим спираль Архимеда, является постоянство расстояний между соседними витками. Каждое из них равно 2πa. Действительно, если угол φ увеличивается на 2π, т.е. точка делает один оборот против часовой стрелки, то радиус увеличивается на 2πa, что и составляет расстояние между соседними витками. График в полярной системе координат на рисунке 1.рис.1

рис.1

Уравнение спирали Архимеда в декартовых координатах будет иметь вид

Рассмотрим как найти площадь, ограниченную спиралью Архимеда, заданной аналитически как r=aφ и двумя радиусами–векторами, которые соответствуют полярным углам φ₁ и φ₂ (φ₁<φ₂). Для решения, площадь, ограниченная кривой r = f(φ) вычислим по формуле , где α и β – пределы изменения полярного угла, тогда получим

(*)

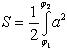
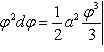
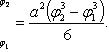Из формулы (*) следует, что площадь, ограниченная полярной осью и первым витком спирали Архимеда (φ₁ = 0; φ₂ = 2π): .Аналогичным образом, находим площадь, ограниченную полярной осью и вторым витком спирали Архимеда ,когда φ₁= 2π;φ₂= 4π.

Получаем ответ, соответствующий разности вычисленных площадей.

Следующая из рассматриваемых в статье кривых будет Лемниската Бернулли, название которой происходит от древнегреческого слова λημνίσκος – лента, повязка. В Древней Греции «лемнискатой» называли бантик, с помощью которого прикрепляли венок к голове победителя на спортивных играх. Данный вид лемнискаты назван в честь швейцарского математика Якоба Бернулли, положившего начало её изучению. [2]Лемниската давала, по мнению Я. Бернулли, решение одной механической задачи. Уравнение лемнискаты впервые опубликовано в статье Я. Бернулли «Curvatura Laminae Elasticae» в журнале «Acta eruditorum» в 1694 году. Здесь Бернулли и назвал эту кривую lemniscus. Он не знал, что четырнадцатью годами ранее, Дж. Кассини уже исследовал более общий случай такой кривой, а квадратуру лемнискаты впервые исследовал Д.К.Фаньяно, опубликовав в 1718 году статью «Metodo per misurare la lemniscata», положив тем самым начало изучению эллиптических интегралов, продолженное впоследствии Л. Эйлером. Некоторые свойства кривой были также исследованы Штейнером в 1835 году. [3]. Лемниската Бернулли представляет геометрическое множество точек на плоскости, произведение расстояний от которых до двух заданных точек фокусов постоянно и равно квадрату половины расстояния между фокусами. Уравнение лемнискаты в прямоугольной системе координат имеет следующий вид: (x² + y² )² = 2a² (x² - y² ) , а в полярной: r² = a²cos 2φ . График, напоминающий знак «бесконечности» в математике, изображен на рисунке 2.

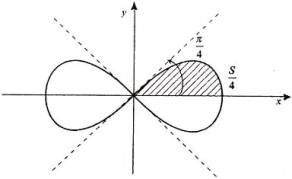рис.2

Вычислим площадь, заключенную внутри лемнискаты Бернулли . В полярной системе координат площадь фигуры, ограниченной дугой кривой r = f(φ) и двумя полярными радиусами φ₁ = α и φ₂ = β , выразится интегралом

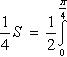
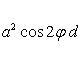
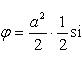
В силу симметрии кривой определяем сначала одну четвертую искомой площади 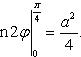, тогда вся площадь равна S = a²..

«Улитка Паскаля» или лимакона – кривая, которая относится к кривым четвертого порядка – конхоидам. Эта кривая была названа Робервалем «улиткой Паскаля», в честь Этьена Паскаля, отца Блеза Паскаля. [3]. Улитка Паскаля – геометрическое место точек М и М1, расположенных на прямых пучка с центром в точке О, лежащей на данной окружности радиуса R, и находящихся на равном расстоянии по обе стороны от точки пересечения Р прямых пучка с окружностью, где расстояние а < 2R.Линия задаётся уравнениям в прямоугольных координатах (

(x² + y² + 2ax)² = 4а² (x² + y² ) , или в полярных координатах r = 2a(1-cos φ) , графиком имеет следующую фигуру, изображенную на рисунке 3.

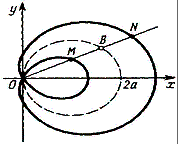рис.3

Другая кривая – астроида относится к циклоидам. Циклоидами занимались многие выдающиеся математики. Название «циклоида» принадлежит Галилео Галилею, он его дал линии в 1598 году. Точно вычислил площадь циклоиды Роберваль в 1634 году, результат которого подтвердили Декарт и Ферма 1638году. Название кривой «астроида» предложил австрийский астроном Карл Людвиг фон Литров в1838году. [4]. Астроида – плоская кривая, описываемая точкой окружности радиуса r, катящейся по внутренней стороне окружности радиуса R = 4r ,показана на рисунке 4.Кривая задается уравнениями в декартовых координатах:в параметрическом виде Вычислим длину дуги астроиды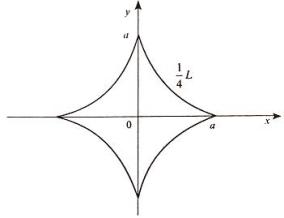рис.4

В уравнении (x^1/3)²+ (y^1/3)²= (a^1/3)²положим x^1/3 = a^1/3cos t, y^1/3 =a^1/3sint, получаем параметрические уравнения астроиды x=acos³t, y=asin³t,(**), где 0 ≤t≤ 2π. Ввиду симметрии кривой (**) достаточно найти одну четвертую часть длины дуги L, при изменении параметра t от 0 до π/2. Получим dx=-3acos²tsintdt, dy=3asin²tcostdt, находим Интегрируя полученное выражение в пределах от 0 до π/2, вычислим

,отсюда L= 6a.

Рассмотрим далее плоскую кривую, название которой – «Декартов лист». Впервые уравнение этой кривой исследовал Р. Декарт в 1638 году, однако он построил только петлю в первом координатном квадранте, где координаты принимают положительные значения. Декарт полагал, что петля симметрично повторяется во всех четырёх координатных четвертях, в виде четырёх лепестков цветка. Форма кривой была впервые определена Робервалем, который находит узловую точку кривой, однако в его представлении кривая состоит лишь из петли. Повторяя эту петлю в четырех квадрантах, он получает фигуру, напоминающую цветок с четырьмя лепестками. В то время эта кривая называлась цветком жасмина (англ. jasmine flower, фр. fleur de jasmin), который Декарт "подарил" своему другу П. Ферма. Полная форма кривой с наличием асимптоты, проходящей через точки (–а, 0) и (0, –а), была определена позднее в 1692 году Гюйгенсом и И. Бернулли. [5]. установилось только с начала 18 века. Название «Декартов лист» прочно установилось только с начала 18 века. 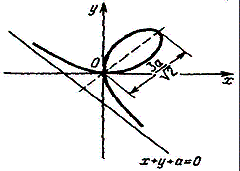рис.5

Декартов лист - плоская кривая, удовлетворяющая уравнению в прямоугольной системе x³ + y³ = 3axy,график выглядит как на рисунке 5. В современной математике кривые высших порядков делятся на алгебраические и трансцендентные, их изучение сыграло и имеет важную роль в аналитической геометрии, дифференциальном, интегральном исчислении, механике, оптике, астрономии.

Литература

1. Рыбников К. А. История математики: Учебник.–М.: Изд-во МГУ, 1994.–496 с.

2. Юшкевич А.П. История математики в средние века. М.: Физматгиз. 1981. 3 3.Вилейтнер Г. История математики от Декарта до середины XIX столетия. М.: Физматгиз. 1960.467 с.

4. http://matematikaiskusstvo.ru/ 5.ru.wikipedia.org