ANALIZA ZMIENNEJ LOSOWEJ SKOKOWEJ NA PRZYKŁADZIE LICZBOWYM

ANALYSIS OF RANDOM VARIABLE DISPLACEMENT WITH
A NUMERCIAL EXAMPLE

Katarzyna Brożek

STRESZCZENIE: Prezentowany artykuł stanowi swoistego rodzaju powtórzenie
i ugruntowanie wiedzy z pewnego wycinka statystyki opisowej, mianowicie dotyczy zmiennej losowej skokowej. Wyznaczono dwa generalne cele pracy, pierwszym była analiza rozkładu zmiennej losowej skokowej (wykorzystując przy tym wybrany przykład liczbowy). Natomiast drugim celem opracowania było zbadanie oraz interpretacja podstawowych parametrów na podstawie uzyskanych wyników z obliczeń własnych. Rozważania kierowane są szczególnie do studentów ekonomii nie zaś statystyki, gdyż analiza nie jest wyczerpująca, a przy tym zakres tematyczny jest zawężony.

Słowa kluczowe: parametry, statystyka opisowa, zmienne losowe skokowe

SUMMARY: The article is a kind of repetition and consolidating the knowledge of a certain segment of descriptive statistics, namely it concerns the random variable displacement. Two general objectives of the work were set, the first was to analyze the distribution of the random variable displacement (by taking advantage of the chosen numerical example). While the second objective of the study was to investigate and interpret the basic parameters on the basis of the results of own calculations. The considerations are addressed especially to students of economics rather than statistics, since the analysis is not exhaustive, and at the same thematic scope is narrowed.

Key words: parameters, descriptive statistics, random variables displacement

WPROWADZENIE

Prezentowany artykuł traktuje o zmiennych losowych, niemniej jednak główna uwaga jest skupiona na zmiennych losowych skokowych, zaś na temat zmiennych losowych ciągłych tylko krótko wspomniano. Tak też w pierwszej części opracowania zaprezentowano najważniejsze informacje o tych dwóch rodzajach zmiennych, natomiast pozostałą część rozważań poświęcono na omówienie rozkładu zmiennej losowej skokowej oraz podstawowych jej parametrów. Wobec tego obliczono dystrybuantę, wartość przeciętną, wariancję i odchylenie standardowe. Jednakże
w ostatniej części analizy zaprezentowano oraz zinterpretowano wyniki dotyczące współczynnika zmienności, dominanty, mediany, asymetrii oraz kwartyli.

ZMIENNE LOSOWE SKOKOWE A ZMIENNE LOSOWE CIĄGŁE

Zmienne losowe charakteryzują się tym, iż z góry nie można przewidzieć ich realizacji. Wartości jakie przyjmują zależą od przypadku. Zmienna losowa jest funkcją, ponieważ każdej jej możliwej wartości przypisane jest w sposób jednoznaczny określone prawdopodobieństwo jej realizacji. Zmienna losowa skokowa (rys. 1) określana jest na zbiorach skończonych lub przeliczalnych (najczęściej jest to zbiór liczba naturalnych), charakteryzuje się tym, że w danym obszarze jej realizacji może przyjąć tylko niektóre wartości [Krysicki, Bartos i in., 1997, s. 50,55].

Punkt skokowy

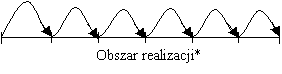
* pomiędzy punktami skokowymi zmienna nie przyjmuje wartości; nie realizuje się

Rysunek 1 Interpretacja graficzna - zmienna losowa skokowa (dyskretna)

Źródło: opracowanie własne

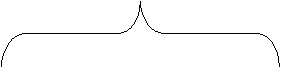Natomiast zmienna losowa ciągła (rys. 2) jest określona na zbiorach nieskończonych (najczęściej jest to zbiór liczb rzeczywistych) i charakteryzuje się tym, że na danym obszarze jej realizacji może przyjąć wszystkie możliwe wartości [szerzej Koronacki, Mielniczuk, 2001].

Obszar realizacji*

* każda wartość może być przyjęta

Rysunek 2 Interpretacja graficzna - zmienna losowa ciągła

Źródło: opracowanie własne

Zmienna losowa skokowa definiowana jest poprzez podanie rozkładu jej prawdopodobieństwa - (tab. 1) oraz dystrybuantę. Prawdopodobieństwo P(x) jest miarą zdarzenia losowego, a ponadto jest liczbą rzeczywistą z przedziału <0,1> [Jakubowski, Sztencel, 2004, 59].

Tabela 1 Rozkład prawdopodobieństwa zmiennej losowej skokowej

xi	x1	x2	…	xk	∑
p(xi)	p(x1)	p(x2)	…	p(xk)	1,0

Źródło: opracowanie własne na podstawie [Piontek, s. 6]

gdzie:

xi – możliwe realizacje zmiennej

p(x_i) – prawdopodobieństwo realizacji danej wartości zmiennej

Dystrybuanta zmiennej losowej skokowej jest definiowana jako prawdopodobieństwo tego, że zmienna losowa przyjmuje wartość nie większą niż argument tej dystrybuanty [Makowiecki, 2016].

F (x) = P (X < x) =

Własności dystrybuanty [zob. Ostasiewicz, Rusnak, Siedlecka, 1998]:

· Jest ona funkcją;

· Zawsze przyjmuje wartości F(x_i) ≤ 1;

· Jest funkcją przynajmniej lewostronnie ciągłą;

· F (–∞) = 0; F (+∞) = 1;

F (–∞) = P (X < –∞) = 0 zdarzenie niemożliwe (więc prawdopodobieństwo równe 0);

F (+∞) = P (X < +∞) = 1 zdarzenie pewne.

Wartość oczekiwana, przeciętna - (nadzieja matematyczna) – jest sumą iloczynów wartości zmiennej i ich prawdopodobieństw [Patan, s. 7].

Wariancja informuje o tym jak duże jest zróżnicowanie wyników w danym zbiorze.
W uproszczeniu można przyjąć, iż odchylenie standardowe jest pierwiastkiem z wariancji.

Dominanta jest to ta wartość zmiennej, która realizuje się z największym prawdopodobieństwem:

Max p(x_i) D = x_i

Mediana jest wartością środkową bądź kwartylem drugim [Tarasiuk, 2013, s.13].

Współczynnik zmienności określa stopień zróżnicowania.

Asymetria rozkładu zmiennej skokowej może być:

a) lewa A < 0, gdy bardziej prawdopodobne są te wartości zmiennej, które są większe od jej wartości oczekiwanej, E(x) < D;

b) prawa A > 0, gdy bardziej prawdopodobne są te wartości zmiennej, które są mniejsze od wartości oczekiwanej, E(x) > D;

c) symetria / rozkład symetryczny A = 0, E(x) = D.

Poniżej umieszczono treść przykładowego zadania poddanego analizie.

W przedsiębiorstwie handlowym X wylosowano 1000 pracowników, zatrudnionych w dziale sprzedaży. Kierownictwo w ciągu roku kontrolowało liczbę ich nieobecności. Wyniki przeprowadzonej analizy zawiera tabela nr 2. Zakładając, że liczba nieobecności jest zmienną losową, podano jej rozkład, dystrybuantę oraz obliczono wybrane parametry.

Tabela 2 Rozkład zmiennej losowej skokowej oraz wybranych parametrów

liczba nieobecności xi	0	1	2	3	4	5	6	7	8	9	10
liczba pracowników	248	202	165	137	96	74	42	19	11	5	1	∑ 1000
P (xi) rozkład prawdopod.	0,248	0,202	0,165	0,137	0,096	0,074	0,042	0,019	0,011	0,005	0,001	∑ 1
F (x) dystrybuanta	0	0,248	0,45	0,615	0,752	0,848	0,922	0,964	0,983	0,994	0,999
wartość przeciętna xi*p(xi)	0	0,202	0,33	0,411	0,384	0,37	0,252	0,133	0,088	0,045	0,01	m= 2,225
(xi-m)^2	4,95	1,5	0,05	0,6	3,15	7,7	14,25	22,8	33,35	45,9	60,45
(xi-m)^2*pi	1,228	0,303	0,008	0,082	0,302	0,570	0,599	0,433	0,367	0,230	0,060	∑= 4,182

Źródło: Obliczenia własne

ANALIZA PARAMETRÓW ZMIENNEJ LOSOWEJ SKOKOWEJ

1. WARTOŚĆ OCZEKIWANA, przeciętna – (nadzieja matematyczna)

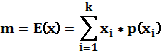2,225 4,950625

2. WARIANCJA I ODCHYLENIE STANDARDOWE

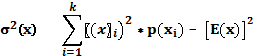
∑ = 4,182

Odchylenie standardowe

√4,182 2,045

3. WSPÓŁCZYNNIK ZMIENNOŚCI

0,9191 92% tyle wynosi stopień zróżnicowania

4. DOMINANTA

D = M₀ = 0 największe prawdopodobieństwo wystąpienia

5. MEDIANA

Me = M = 2 Me = P = (x ≤ 1/2) Me = P = (x ≥ 1/2)

6. ASYMETRIA

1,088

A > 0 asymetria prawa: bardziej prawdopodobne są te wartości zmiennej, które są mniejsze od
wartości oczekiwanej.

7. KWARTYLE

kwartyl pierwszy Q₁ = 1 P (X ≤ Q₁) ≥ 1/4 i P (X ≥ Q₁) ≥3/4

kwartyl drugi – mediana Q₂ = 2 P (X ≤ Q₂) ≥ 1/2 i P (X ≥ Q₂) ≥1/2

kwartyl trzeci Q₃ = 3 P (X ≤ Q₃) ≥ 3/4 i P (X ≥ Q₃) ≥1/4

Na koniec analizy postanowiono wymienić własności zmiennej losowej skokowej:

· P (a ≤ X < b) = F(b) – F(a)

· P (a < X ≤ b) = F(b) – F(a) + P (X = b)

· P (X < a) = F(a)

· P (X ≤ a) = F(a) +P (X = a)

· P (X ≥ a) = 1 – P (X < a) = 1 – F(a)

· P (X > a) = 1 – P (X ≤ a) = 1 – F(a) +P (X = a)

WYNIKI PŁYNĄCE Z PRZEPROWADZONEJ ANALIZY:

· wartość przeciętna wynosi 2,225;

· wariancja stanowi 4,182; zaś odchylenie standardowe 2,045;

· współczynnik zmienności to 92%;

· dominanta wynosi 0, natomiast mediana 2;

· współczynnik asymetrii 1,088.

BIBLIOGRAFIA

[1] JAKUBOWSKI J., SZTENCEL R., Wstęp do teorii prawdopodobieństwa, SCRIPT, Warszawa 2004

[2] KORONACKI J., MIELNICZUK J., Statystyka dla studentów kierunków technicznych
i przyrodniczych, Wydawnictwo Naukowo-Techniczne, Warszawa 2001

[3] KRYSICKI W., BARTOS J., DYCZKA W., KRÓLIKOWSKA K., WASILEWSKA M., Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, Wydawnictwo Naukowe PWN, Warszawa 1997

[4] MAKOWIECKI M., Statystyka matematyczna. Wprowadzenie do rozkładów zmiennych losowych, artykuł dostępny na stronie internetowej https://pl.m.wikibooks.org, [dostęp 10.01.2016]

[5] OSTASIEWICZ S., RUSNAK Z., SIEDLECKA U., Statystyka – elementy teorii
i zadania, Wydawnictwo Akademii Ekonomicznej im. Oskara Langego, Wrocław 1998

[6] PATAN M., Zmienne losowe dyskretne, Instytut Sterowania i Systemów Informatycznych, Uniwersytet Zielonogórski, Zielona Góra

[7] PIONTEK K., Zmienne losowe. Rozkłady ciągłe. Rozkłady dyskretne. Studium podyplomowe Analityk Finansowy, Uniwersytet Ekonomiczny we Wrocławiu, Wrocław

[8] TARASIUK J., Statystyka Inżynierska. Dyskretne i ciągłe rozkłady jednowymiarowe, AGH, WFiIS, Kraków 2013

Katarzyna Brożek, doktorantka Wydziału Ekonomicznego

Uniwersytet Technologiczno-Humanistyczny im. K. Pułaskiego w Radomiu

adres: Polska, Radom, ul. Chrobrego 42/10

tel. kom.: 504 174 290

e-mail: kania6669@wp.pl