Сизоненко В.Л., Масленников Д.И.
Харьковский национальный аграрный университет
имени В.В. Докучаева
К ТЕОРИИ БУНЕМАНОВСКОЙ НЕУСТОЙЧИВОСТИ
ПЛАЗМЫ В МАГНИТНОМ ПОЛЕ
При наложению на плазму сильного
внешнего электрического поля Е,
удовлетворяющего неравенству ![]() , электроны плазмы уходят «в просвист», так что их
направленная скорость
, электроны плазмы уходят «в просвист», так что их
направленная скорость ![]() становится больше тепловой скорости электронов
становится больше тепловой скорости электронов ![]() (здесь
(здесь ![]() и
и ![]() - электрический заряд и масса электрона,
- электрический заряд и масса электрона, ![]() -
плазменная частота ионов). В этом случае в плазме возможно развитие
неустойчивости, открытой Пирсом [1] - [3] и развитой затем в многочисленных
работах (см. [4] - [7] и др.). Она получила название бунемановской
неустойчивости. Именно при таких напряженностях электрических полей в
экспериментах наблюдалось появление второго «плато» на проводимости плазмы,
интерпретируемое как проявление бунемановской неустойчивости [8] , [9]. В замагниченной
плазме эта неустойчивость исследовалась в работах [6], [10]. Моделирование на ЭВМ показало, что для
неустойчивости электроны плазмы остаются холодными даже в режиме сильной
нелинейности колебаний, когда возникают эффекты самопересечения траекторий [3].
Но при этом с самого начала был исключен механизм стохастического нагрева
частиц, рассмотренный в работе [11]. Этот механизм в случае бунемановской
неустойчивости и плазмы без магнитного поля был исследован в работе [12], в
которой обнаружено сильное торможение потока электронов с переходом почти
половины их кинетической энергии в температуру этих частиц.
-
плазменная частота ионов). В этом случае в плазме возможно развитие
неустойчивости, открытой Пирсом [1] - [3] и развитой затем в многочисленных
работах (см. [4] - [7] и др.). Она получила название бунемановской
неустойчивости. Именно при таких напряженностях электрических полей в
экспериментах наблюдалось появление второго «плато» на проводимости плазмы,
интерпретируемое как проявление бунемановской неустойчивости [8] , [9]. В замагниченной
плазме эта неустойчивость исследовалась в работах [6], [10]. Моделирование на ЭВМ показало, что для
неустойчивости электроны плазмы остаются холодными даже в режиме сильной
нелинейности колебаний, когда возникают эффекты самопересечения траекторий [3].
Но при этом с самого начала был исключен механизм стохастического нагрева
частиц, рассмотренный в работе [11]. Этот механизм в случае бунемановской
неустойчивости и плазмы без магнитного поля был исследован в работе [12], в
которой обнаружено сильное торможение потока электронов с переходом почти
половины их кинетической энергии в температуру этих частиц.
В настоящей работе исследована нелинейная стадия возбуждения бунемановской
неустойчивости в замагниченной плазме в предположении, что электрические поля ![]() колебаний создаются
разделенными в пространстве волновыми пакетами, проходя которые частицы плазмы
получают случайные приращения скоростей
колебаний создаются
разделенными в пространстве волновыми пакетами, проходя которые частицы плазмы
получают случайные приращения скоростей ![]() («толчки») (см. [11]
- [13]). В работе [14] показано, что в магнитоактивной плазме система
нелинейных уравнений для средних скоростей электронов
(«толчки») (см. [11]
- [13]). В работе [14] показано, что в магнитоактивной плазме система
нелинейных уравнений для средних скоростей электронов ![]() и ионов
и ионов ![]() вдоль внешнего
магнитного поля
вдоль внешнего
магнитного поля ![]() и для среднеквадратических флуктуаций скоростей
и для среднеквадратических флуктуаций скоростей ![]() и
и ![]() в отличие от [12]
имеет следующий вид:
в отличие от [12]
имеет следующий вид:
 , (1)
, (1)
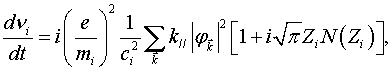 (2)
(2)
 (3)
(3)
 (4)
(4)
где ![]() массы электронов, ионов,
массы электронов, ионов, ![]() Фурье-компонента потенциала
Фурье-компонента потенциала ![]() с волновым вектором
с волновым вектором ![]() и
и ![]() продольная и
поперечная составляющая вектора
продольная и
поперечная составляющая вектора ![]() относительно магнитного поля
относительно магнитного поля ![]() комплексная частота, состоящая из реальной
комплексная частота, состоящая из реальной ![]() и мнимой
и мнимой ![]() частей,
частей, ![]() функция Крампа:
функция Крампа:
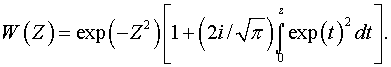
При выводе уравнений (1) - (4)
предполагалось, что ионы незамагничены ![]() , а электроны достаточно холодные
, а электроны достаточно холодные ![]() . Их поперечная энергия
. Их поперечная энергия ![]() предполагалась малой
предполагалась малой ![]() так что для
так что для ![]() справедливо уравнение
справедливо уравнение
 (5)
(5)
Напоминаем, что  где
где ![]() и
и ![]() приращения скоростей ионов и
электронов (вдоль магнитного поля) при их многократных рассеяниях на волновых
пакетах со случайными фазами, а символ
приращения скоростей ионов и
электронов (вдоль магнитного поля) при их многократных рассеяниях на волновых
пакетах со случайными фазами, а символ ![]() означает усреднение
по всему объему плазмы или по нормальным распределениям этих величин [12] -
[14]. Фактически
означает усреднение
по всему объему плазмы или по нормальным распределениям этих величин [12] -
[14]. Фактически ![]() температура ионов плазмы, а
температура ионов плазмы, а ![]() продольная температура электронов.
продольная температура электронов.
Кроме (1) – (5) имеет место
дисперсионное уравнение для волн
![]() (6)
(6)
где


![]() плотность частиц
плазмы,
плотность частиц
плазмы, ![]() угол между
угол между ![]() и
и ![]()
В случае ![]() уравнение (6)
переходит в известное дисперсионное уравнение линейной теории [6], [10]
уравнение (6)
переходит в известное дисперсионное уравнение линейной теории [6], [10]
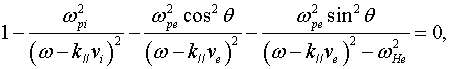 (7)
(7)
в котором скорости ![]() и
и ![]() изменяются согласно уравнениям (1), (2).
изменяются согласно уравнениям (1), (2).
Отбрасывая в (7) второе слагаемое и полагая ![]() в третьем и
четвертом, найдем те значения
в третьем и
четвертом, найдем те значения ![]() , при которых волны нарастают наиболее быстро:
, при которых волны нарастают наиболее быстро:
 (8)
(8)
где ![]() . Удерживая теперь отброшенные члены, получим частоту
. Удерживая теперь отброшенные члены, получим частоту ![]() и инкремент
и инкремент ![]() колебаний:
колебаний:
![]() (9)
(9)
где ![]()
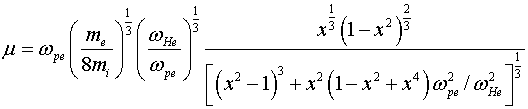 .
.
Из (8), (9) следует, что при ![]() возбуждаются волны с
возбуждаются волны с
![]() (10)
(10)
для которых по порядку величины
справедливы оценки [6]:
 (11)
(11)
При этом из (1) – (5) нетрудно
получить, что ![]()
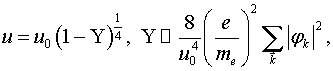 (12)
(12)
 , (13)
, (13)
![]() (14)
(14)
где ![]() и
и ![]() - начальные (при
- начальные (при ![]() ) скорость электронов и их поперечная тепловая скорость
соответственно. Аналогично, для величин
) скорость электронов и их поперечная тепловая скорость
соответственно. Аналогично, для величин ![]() и
и ![]() при выполнении
условий (11) – (14) справедливы оценки
при выполнении
условий (11) – (14) справедливы оценки
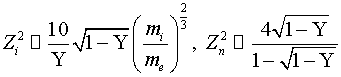 . (15)
. (15)
Из (15) следует, что при ![]() соотношения (10) –
(14) справедливы, и наблюдается сильное торможение электронного потока вплоть
до значений
соотношения (10) –
(14) справедливы, и наблюдается сильное торможение электронного потока вплоть
до значений
![]() (16)
(16)
При этом поперечная энергия
электронов остается малой.
В случае ![]() взаимодействие
электронов с колебаниями приобретает кинетический характер
взаимодействие
электронов с колебаниями приобретает кинетический характер ![]() , когда соотношения (1), (4), (5), (7) становятся
непригодными. Можно, однако, надеяться, что при
, когда соотношения (1), (4), (5), (7) становятся
непригодными. Можно, однако, надеяться, что при ![]() произойдет полная
стабилизация неустойчивости с неизбежным торможением потока электронов. В этом
случае следует ожидать, что около 50% начальной кинетической энергии электронов
уйдет в их тепло, а остальная часть – в колебания плазмы.
произойдет полная
стабилизация неустойчивости с неизбежным торможением потока электронов. В этом
случае следует ожидать, что около 50% начальной кинетической энергии электронов
уйдет в их тепло, а остальная часть – в колебания плазмы.
Литература
1. Pierce T.R. // Journ. Appl. Phys. 1948. v. 19. p. 231.
2. Buneman O. // Phys. Rev. Lett. 1958. v. 1. p. 104.
3. Buneman O. // Phys. Rev. Lett. 1959. v. 115. p. 503.
4.
Будкер Г.И. // Атомная Энергия. 1956. № 5. с. 9.
5.
Коврижных
Л.М., Рухадзе А.А. // ЖЭТФ. 1960. т. 38. с. 850.
6.
Степанов
К.Н. Сб. «Физика плазмы и проблема управляемого термоядерного синтеза» - Киев:
Изд. АН УССР, 1963.
7.
Ловецкий
Е.Е., Рухадзе А.А. Сб. «Физика плазмы». Труды ФИАН СССР. – М.: Наука, 1966.
8.
Бурченко
П.Я., Василенко Б.Т., Волков Е.Д. и др. // Письма в ЖЭТФ. 1966. т. 3. с. 243.
9.
Hamberger S.M., Friedman M. //Phys. Rev. Lett. 1968. v. 21. p.674.
10.
Buneman O. // J. Nucl. Energy Pt. 1962. v. 4. p. 111.
11.
Сизоненко В.Л. // Вопросы Атомной Науки и
Техники. Харьков. 2008. № 4. с. 250.
12.
Сизоненко
В.Л. Торможение и нагрев потоков плазмы в стохастических электрических полях //
Физика Плазмы. 2009 (в печати).
13.
Сизоненко
В.Л. // Мат. Ш Международной научно-практической конференции «Науковий потенціал світу - 2006». Днепропетровск. 2006. т. 9. с.
73.
14.
Сизоненко
В.Л. Теория взаимодействия плазмы со стохастическими электромагнитными полями.
// Физика Плазмы. 2009 (в печати).
Сизоненко Владимир Леонидович
Заведующий кафедрой высшей
математики
Харьковского национального
аграрного университета им. В.В. Докучаева
Доктор физ.-мат. наук, профессор
Телефон: 99-75-80
E-mail: lyuba-sizonenko@mail.ru.
Масленников Дмитрий Игоревич
Доцент кафедры высшей математики
Харьковского национального
агарного университета им. В.В. Докучаева
Кандидат физ.-мат. наук, доцент
Телефон: 99-75-80