Технические науки, отраслевое машиностроение

Вайтехович П.Е., Францкевич В.С.

Белорусский государственный технологический университет

Определение оптимальной частоты вращения размольной тарелки среднеходной мельницы

В последнее время в зарубежной практике четко обозначилась тенденция применения в крупнотоннажных производствах валково-тарельчатых (среднеходных) мельниц. Размол материала в них происходит преимущественно за счет раздавливания и дополнительно за счет истирания между столом и валками или шарами.

Анализ движения материала по вращающейся тарелке показывает, что при его подаче в центр тарелки образуется слой определенной толщины, закономерности движения которого описываются с помощью механики сыпучей среды или механики грунтов.

Уравнение для расчета формы образующей слоя предлагается в виде [1]:

, (1)

где f₀ - коэффициент внутреннего трения среды; w, – угловая скорость размольной тарелки; r, r₀ − соответственно текущий радиус и предельный радиус равновесия; z − осевая координата.

С использованием уравнения (1) мы привели расчет высоты слоя материала и его распределения по радиусу вращающейся тарелки при различных угловых скоростях. В результате расчета (рис. 1) получены профили распределения сыпучего материала по вращающейся тарелке. Анализ этих профилей показывает, что с увеличением угловой скорости размеры условного конуса сыпучего материала (высота и диаметр) уменьшаются, что обусловлено ускоряющимся распределением материала в виде тонкого монослоя по вращающейся тарелке под воздействием инерционных центробежных сил. Графические зависимости z = f(r) имеют практическую значимость для дальнейшего анализа движения частиц. Проведя горизонтальную прямую, соответствующую диаметру подаваемых на измельчение частиц, по точкам ее пересечения с кривыми конкретного профиля распределения можно определить начальный радиус, при котором образуется монослой этих частиц. Причем каждую частицу в монослое можно рассматривать как одиночную, а началом отсчета ее движения и будет определенный таким образом радиус.

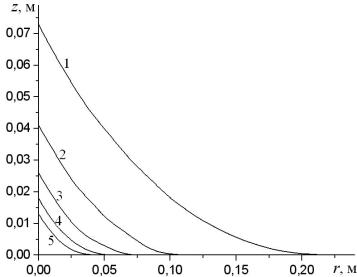
1 − 6 рад/с; 2 − 8 рад/с; 3 − 10 рад/с; 4 − 12 рад/с; 5 − 14 рад/с

Рис. 1. Профиль распределения сыпучего материала по тарелке

при различных угловых скоростях

Далее при движении от центра к периферии высота слоя постепенно уменьшается до значения, равного диаметру наибольшей частицы. В идеале частицы должны попадать под валок в один слой без контакта между собой. На этом участке можно рассматривать движение одиночной частицы, уравнение движения которой имеет вид:

, (2)

где F_Т − сила трения частиц по тарелке; F_1т – сила трения частиц между собой; F_с – кориолисова сила инерции; F_e – переносная (центробежная) сила инерции.

Силу трения частиц между собой можно определить через нормальную реакцию, возникающую от давления одной частицы на другую, обусловленного инерционными силами. Исходя из расчетной схемы (рис. 2), эта сила:

F_1т = f₁N = f₁(F_esiny − F_c). (3)

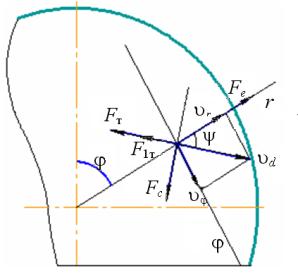
Рис. 2. Расчетная схема движения частиц по тарелке

Уравнение (2) в проекциях на подвижные полярные оси примет вид [2]:

(4)

Для гарантированного измельчения материала необходимо, чтобы за время поворота тарелки от одного валка к другому, частица обязательно попала под один из них. В радиальном направлении этот путь перемещения не должен превышать ширину валка. Условие гарантированного попадания частиц материала под валок можно определить из решения общих уравнений движения. Для этого необходимо зафиксировать время пересечения частицы с окружностью, проходящей через внутренние кромки валков, а затем проконтролировать ее перемещение в радиальном направлении Δr за время t = 1/2n, где n - частота вращения тарелки. Тогда условие гарантированного попадания частиц материала под валки будет Δr £ B, где B = 0,2D - ширина валка, принимаемая в зависимости от диаметра тарелки. На рис. 3 представлена зависимость радиального перемещения частицы Δr от частоты вращения, которая определялась как величина, обратная времени: n = 1/2t.

Если провести горизонтальную прямую, соответствующую ширине валка B, то участок кривой, расположенный под ней, включает диапазон частот с гарантированным попаданием частиц материала под размольный валок.

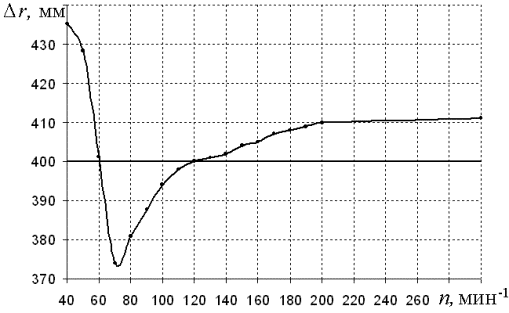
Рис. 3. Зависимость радиального перемещения частицы

от частоты вращения тарелки

Таким образом, модель движения твердых частиц по размольной тарелке и ее решение дали возможность установить условие гарантированного попадания материала под валок, определить траекторию движения частиц и все ее параметры (скорость, угол) на выходе с тарелки и установить оптимальный диапазон частот вращения рабочего органа.

Список литературы

1. Маркман, Я.Б. К расчету движения материала на размольной тарелке вертикальной роликовой мельницы. Сб. науч. тр. / ВНИИцеммаш. / Я.Б. Маркман, В.И. Силкина. –Тольятти, 1985. – С. 58–67.

2. Францкевич, В.С. Определение траектории движения материала по размольной тарелке валково-тарельчатой мельницы / В.С. Францкевич, П.Е. Вайтехович // Труды БГТУ. Сер. III, Химия и технология неорган. в-в / Бел. гос. технол. у-т. − Минск – 2007. − Вып. XV.– С. 149–152.