MATHEMATICAL MODELING OF SPREAD OF CONCENTRATION IN STRATOSPHERE FROM
EXPLOITATION OF CARRIER ROCKETS
ISAKHOV A., ZHAKEBAEV D., ZHUBAT K.
In
this paper the modeling of distribution of rocket fuel components in the atmosphere
is studied. On the basis of the Navier-Stokes equations a mathematical model of
impurity migration process in the stratified medium was developed. The
numerical algorithm was worked out using a scheme of splitting on physical
parameters. Modeling of rocket fuel components distribution in surface layer of
the atmosphere and in stratosphere was carried out. Results of modeling are
presented in the form of three dimensional graphs.
Components
of modern rocket-and-space equipment, especially carrier rockets, constitute a
serious danger for environment due to considerable reserves of high-energy
chemical fuel. For example, in the process of launch of “Proton-M” carrier
rocket the projected scope of emission to the atmosphere of remnants of crude heptyl
from stage 1 and 2 amounts to 1,7 tons, and in case of the carrier rocket
breakdown the emissions of such highly toxic fuel to the atmosphere total tens
of tons. In the surface atmosphere layer up to 1 km from the ground the
emissions resulting from launching of spaceships can lead to acid rains and
weather changes within the area of launching covering up to 200km2. In
the stratosphere at the elevation of 40-60km the processes of mixing are less
intensive what causes contaminations generating at such levels to last longer.
So, aerosol particles emitted by stage 1 of carrier rockets can retain in the
stratosphere for the period of up to one year or longer possibly affecting
thermal balance of the atmosphere.
The
subject of the research work is modeling of distribution of rocket fuel
components in the surface layer of the atmosphere and modeling of the dynamics
of movement and transformation of aerosol cloud in the stratosphere formed in
the process of draining of the first stage of the carrier rocket.
For
description of processes of migration, diffusion and transformation of impurities
they should be considered on the basis of a physically rich model accounting
for daily course of changes of dispersion depending on meteorological fields,
orographic, thermal heterogeneities of underlying surface, turbulent features
of the atmosphere [1] and so on. In mathematical modeling impurities dispersion
processes a very important stage is development and choice of the corresponding
computational algorithm and approximation of equation of migration.
Mathematical model.
Large-scale movements in the surface layer of the atmosphere are approximately
described by a system of equations including motion equations, equations of
continuity and equations of concentration. This model ensures computation of
fields of velocities and concentration. An advanced turbulent spatial flow is
considered [2,3]. The equations are the following:
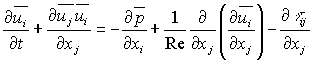 (1)
(1)
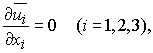 (2)
(2)
where - ![]() (3)
(3)
For modeling of
distribution of rocket fuel components in the surface layer of the atmosphere
the following equation was used:
 (4)
where ui are velocity
components; D diffusions factor; αT
= vt/Pr
(4)
where ui are velocity
components; D diffusions factor; αT
= vt/Pr
Smagorinsky dynamic
model was used as a model of turbulence [4]. For application of the dynamic
model double averaging was conducted with the filter length ∆ = 2∆
then
 (5)
(5)
Equation averaged for
two times with two filters having length [∆ and] has correspondingly the following design:
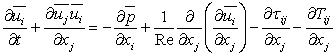 (6)
(6)
where![]() . From (4) and (5) it follows that
. From (4) and (5) it follows that ![]() then
then ![]() has the following:
has the following: ![]() and tensions
and tensions
![]()
From formula (6) using least-squares
method when value C in the form
of 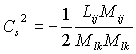 where
where ![]()
Boundary conditions. For the task of
distribution of rocket fuel components in the surface layer of the atmosphere
the following boundary conditions were set:
at the upper boundary of
the air mass:
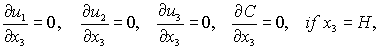
on the ground surface:
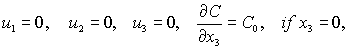
at lateral boundaries:
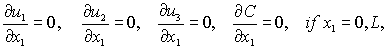

For the task of dynamics
and migration of aerosol cloud resulting from draining of the stage 1 of the carrier
rocket in the stratosphere the boundary conditions are the following:
at the upper boundary of
the air mass:

at the lower boundary:
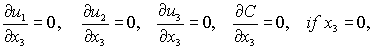
at lateral boundaries:
![]()

Numerical algorithm. For solution of the task
with the account of the proposed model a scheme of splitting on physical
parameters is used [5]. At the first stage it is supposed that carrying over of
movement amount takes place only due to convection and diffusion. Intermediate
field of velocity is determined by rhythmic steps using double-sweep method. At
the second stage the determined intermediate field of velocity is used for
determination of the field of pressure. Poisson equation for the field of
pressure is solved using Fourier method in combination with matrix double-sweep
method used for determination of Fourier factors. At the third stage it is
supposed that migration takes place only due to pressure gradient. Task
algorithm is paralleled on a high-performance system [6,7]:
I) ![]()
II) ![]()
III) ![]()
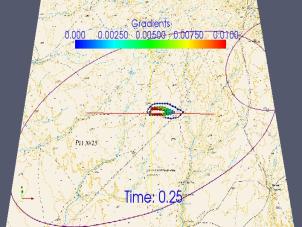
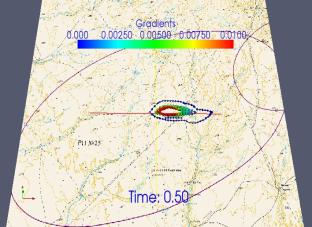
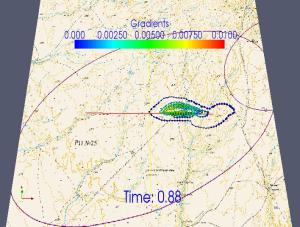
Results of modeling. In Fig.1 contour lines
are depicted denoting concentrations of toxic rocket fuel components (RFC) in
the western wind after regular falling of stage 1 of “Proton-M” carrier rocket
at different time moments.
|
|
|
|
|
|
Fig.1 contour lines are
depicted denoting concentrations of toxic rocket fuel components (RFC) in the
western wind after regular falling of stage 1 of “Proton-M” carrier rocket at
different time moments
As is seen in the
figures, the excitation caused by diffusion-convection flows, extends to the
boundary of the computed area and reaches it in 12-15 hours. Results of
modeling of migration of RFC in the surface layer of the atmosphere show that migration
of heptyl and its spreading rate depend on the direction and force of the wind.
The main contamination site is the area of falling of the carrier rocket’s
stage and the adjacent 100-120 m wide and 150-180 m long ellipse-shaped
territory with integral concentration of 0,25mg/m2. Carrying of
heptyl by winds out of the territory does not exceed maximum permitted
concentrations. Highly concentrated heptyl is found at the site of falling of
the carrier rocket having integral concentration of 1,2 – 1,5mg/m2.
In
the second task a launch of carrier rocket is modeled in the presence of tail
wind with the velocity of 2 m/s. Calculations were executed within rectangular
area with dimensions along both horizontal directions being 20km, and the altitude
totaling 40-60 km. The results of the calculations are shown in fig.2 and 3. On
fig.2 contour lines are depicted showing concentrations of RFC (view from
above) after draining of stage 1 of “Proton-M” carrier rocket.
|
|
|
Fig.2 Contour lines
showing concentrations of RFC (view from above) 1 hour (a) and 6 hours (á) after draining of stage 1 of “Proton-M” carrier rocket. Altitude - 50km,
tail wind, wind velocity amounting to 2m/s.
On
Fig.3 equiscalar surfaces are depicted showing concentrations of RFC after
draining of stage 1 of “Proton-M” carrier rocket at the altitude of 50 km at
different time periods. The results obtained in the course of solving task two
make it noticeable that the concentration of combustion products is spread over
a territory bigger than the dynamic excitation field. As the time passes, the
dynamic field fades away, and concentration field changes its state to the
state of passive impurity and keeps migrating in the stratosphere for a long
period of time. It is also problematic to trace further migration of
concentrations in the stratosphere after their carrying over from the computed
area since it necessitates modeling in larger scales.
|
|
|
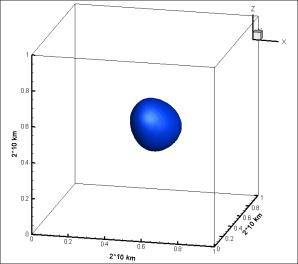
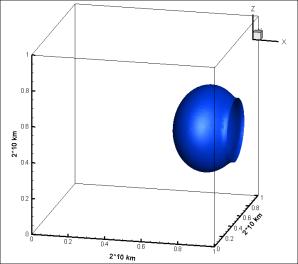
Fig.3 Equiscalar
surfaces showing concentrations of RFC (view from above) 1 hour (a) and 6 hours
(á) after draining of stage 1 of “Proton-M” carrier rocket. Altitude - 50km,
tail wind, wind velocity amounting to 2m/s
Thus, basing on
Navier-Stokes equations a mathematical model of RFC distribution was designed
allowing for modeling the processes of migration either within the surface
layer of the atmosphere or within stratosphere. The obtained results can be
used for monitoring of ecological situations within the areas where carrier
rockets’ falling occur, as well as for prediction of scopes of atmosphere
contamination and assessment of ecological damage caused in relation to the
environment.
References
1.
Penenko
V.V., Aloyan A.E. Models and methods for
solution of problems of environmental protection. Novosibirsk: Nauka (Science),
1985. 256 p.
2.
Fletcher
K. Computation methods in fluid dynamics. 2 editions.
M.: Mir, 1991, Ed.2. 552 p.
3.
Rouch
P. Computational fluid dynamics. M.: Mir, 1972. 612 p.
4.
Lesieur M. Metais O., Comte P. Large
eddy simulation of turbulence. New York: Cambridge University Press, 2005. 219
p.
5.
Yanenko N.N.
Methods of rhythmic steps in solution of multivariate problems mathematical
physics. Novosibirsk: Nauka (Science), 1967. 197 p.
6.
Antonov
A.S. Parallel programming using MPI technologies. M.: MSU,
2004. 71 p.
7.
Shpakovsky
G.I., Serikova N.V. Programming for
multi-processor systems in MPI standards. Minsk: BSU, 2002. 323 p.