УДК
517.977.1
Куракбаев Джумагали Салбекович,
Ибрагимов Бахыт Усманалиевич
Южно-Казахстанский государственный университет, г.Шымкент
Качественные
вопросы Задачи живучести в управляемых системах
Введение. Задача живучести является задачей теории
управления, в определенном смысле противоположная задаче быстродействия. Цель
управления в задаче живучести сводится к тому, чтобы как можно дольше удержать
фазовую точку в пределах заданного множества.
В задаче быстродействия терминальное множество
предполагается, как правило, замкнутым и задача имеет смысл только для
начальных точек, принадлежащих области управляемости. В случае же задачи
живучести окажется естественной замкнутость области выживания, являющейся
дополнением терминального множества, и задачу следует исследовать для любой
начальной точки из области выживания.
При исследовании задачи живучести следует ответить на
следующие вопросы качественного характера, которые рассматривались в данной
статье:
·
существует ли оптимальное управление;
·
является ли множество слабо инвариантным, т.е. для любой начальной точки
существует ли хотя бы одна траектория рассматриваемой управляемой системы,
выходящая из данной точки, определенная на бесконечном интервале времени и
целиком лежащая в данном множестве;
·
существует ли непустое подмножество заданного множества, слабо инвариантное
относительно рассматриваемой управляемой системы.
Отметим, что каждое из перечисленных вопросов
представляет интерес, поскольку они возникают и в других задачах теории
оптимального управления.
Постановка задачи. Пуст дана управляемая
система
(1)
где
–фазовый вектор, 
–вектор управления, принимающий свои значения из области
управления 
, являющаяся
компактным подмножеством 
.
Относительно
функции 
предполагаются, что [1]:
·
–непрерывное отображение 
;
·
для любого компакта 
существует константа 
такая, что для произвольных 
и 
имеет неравенство Липшица
·
существует такая константа 
, что для всех 
, 
справедливо неравенство 
, где 
–знак скалярного произведения;
·
для любого 
вектограмма 
выпукла.
Формулировка задачи. Определение 1. Решением системы
(1) называется функция 
, которая абсолютно непрерывна и удовлетворяет систему 
во всех 
.
Определение 2. Допустимым
управлением системы (1) называется множество всех измеряемых функции вида 
.
Как известно из [2], что при
выше сделанных предположениях для любых 
и 
задача Коши
(2)
имеет единственное решение 
, определенное на 
В дальнейшем обозначаем через 
–непустое подмножество 
, а через 
–терминальное множество, где 
. Для любых 
и 
через 
обозначим максимальную длину
интервала времени 
, на котором траектория 
находится в пределах множества 
, т.е.
для всех 
(3)
Задача живучести в области 
ставится следующим
образом: для начальной точки 
найти такое управление 
, при котором функционал (3) принимает наибольшее значение, т.е. достигает
величины
(4)
Итак, задачу живучести для системы (1) можно
формализовать следующим образом [3]:
(5)
Определение 3. Множество 
называется слабо
инвариантным относительно системы (5), если для любой начальной точки 
существует управление
такое,
что 
для всех 
.
Определение 4. Множество 
называется
сильно инвариантным относительно системы (5), если для любых 
и 
, существует 
при всех 
.
Определение 5. Максимальное подмножества 
, слабо инвариантное относительно системы (5), называется ядром живучести множества 
относительно системы
(5) и обозначается 
.
Установление существования
оптимального управления. В задаче быстродействия,
как правило, терминальное множество 
считается замкнутым. Например, теоремы существования
оптимальных управлений доказываются в предположении замкнутости терминального
множества [4].
В работе [5] было выявлено, что
условия открытости 
является
естественным. Таким образом, в задаче избежания столкновений с замкнутым
терминальным множеством оптимальное управления не существует. Вышеуказанные
теоремы справедливы и в задаче живучести. Следующая теорема [6] также подверждает это.
Теорема [6]. Пусть в задаче (5) терминальное множество 
открыто. Тогда для
любого 
существует оптимальное управление.
Выяснение
слабой инвариантности области выживания. Предполагаем, что 
, где 
- фазовый вектор, 
–постоянная 
–матрица, 
- вектор управления, который принимает свои значения из
компактной выпуклой области управления 
.
Пусть 
означает максимальное подмножество множества 
, сильно инвариантное относительно системы (1), т.е.
.
Через 
обозначим множество
точек покоя системы (1), т.е. 
. Здесь 
–прообраз множества 
при отображении 
. Далее, для линейного подпространства 
пространства 
через 
обозначим максимальное подпространства 
, инвариантное
относительно A, т.е.
.
Теорема 1. Пусть 
–линейное подпространства 
. Тогда справедлива формула
(6)
Доказательство. Возьмем произвольную точку. Тогда по определению
сильно инвариантного множества, в частности, для любого постоянного управления 
имеем
при
всех 
Далее,
воспользовавшись формулой Коши для 
получим
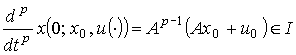
при
всех 
.
Следовательно, 
. Отсюда в силу произвольности 
имеем 
.
Таким
образом,
.
Пусть
теперь 
–произвольная точка, принадлежащей правой части равенства (6). Тогда для произвольного управления 
имеем
поскольку все значения
подынтегральной функции в последнем интеграле принадлежат 
. Теорема доказана.
Следствие.
Пусть 
- линейное подпространство 
. Тогда 
в том и только том
случае, если 
и 
.
Теорема 2. Пусть G –
выпуклый компакт и 
. Тогда 
.
Доказательство.
Возьмем произвольную точку 
. Поскольку выпуклый компакт 
является слабо инвариантным относительно системы
,
то согласно теореме [6]
.
Отсюда в силу
произвольности 
заключаем, что 
.
Теорема доказана.
Выводы. В статье рассматривается инвариантные множества в
управляемых системах. После установление существования оптимального управления,
определяется непустое множества, слабо инвариантное относительно
рассматриваемой управляемой системы.
Из доказанной теоремы, вытекает
необходимое и достаточное условия сильной инвариантности линейного
подпространства.
Литература
1.
Ибрагимов У.М. К теории задачи живучести // Материалы XVI межд. конф. по вычисл. механике и современным
прикладным программным системам (ВМСППС’2009). –Алушта, Крым,
2009. с.332-334.
2.
Филиппов А.Ф. О некоторых вопросах теории оптимального регулирования //
Вестник МГУ. Сер. мат., мех., аст. 1959. №2.
с. 25-32.
3.
Ibragmov U.M. Survival task in controllable systems // Reports of the
third congress of the world mathematical society of turkic countries. Al-Farabi
kazakh national university. Vol 2. –Almaty, «Қазақ университеті», 2009. p. 112-115.
4.
Понтрягин Л.С., Болтянский В.Г., Гамкрелидзе Р.В., Мищенко Е.Ф.
Математическая теория оптимальных процессов. –М.: Наука, 1969. -384 с.
5.
Сатимов Н., Азамов А. К задаче избежания столкновений в нелинейных системах
// ДАН УзССР. 1974. №6, с.3-5.
6.
Фазылов А.З. К задаче избежания столкновений // Изв. АН Уз ССР. Серия физ.-мат.наук. 1987. №3. с. 30-36.