Ленюк М. П.

Чернівецький факультет НТУ „ХПІ”

ГІБРИДНЕ ІНТЕГРАЛЬНЕ ПЕРЕТВОРЕННЯ

ФУР’Є – БЕССЕЛЯ – (КОНТОРОВИЧА - ЛЄБЄДЄВА)

НА ПОЛЯРНІЙ ОСІ

Запровадимо методом дельта-подібної послідовності інтегральне перетворення, породжене на множині

гібридним диференціальним оператором (ГДО)

(1)

Тут - одинична функція Гевісайда [1]; - диференціальний оператор Фур’є [2]; - диференціальний оператор Бесселя [3], - диференціальний оператор (Конторовича - Лєбєдєва)[4], .

Означення. Областю визначення ГДО назвемо множину вектор-функцій з такими властивостями: 1) вектор-функція неперервна на множині ; 2)існують числа та такі, що

(2)

3) функції задовільняють умови спряження

. (3)

Оскільки ГДО самоспряжений і має одну особливу точку , то його спектр дійсний та неперервний. Можна вважати, що спектральний параметр . Спектральна вектор-функція, яка відповідає спектральному параметру , дійсна:

(4)

При цьому функції повинні задовільняти відповідно диференціальні рівняння

(5)

та умови спряження (3);

Фундаментальну систему розв’язків для диференціального рівняння Фур’є утворюють функції та [2]; фундаментальну систему розв’язків для диференціального рівняння Бесселя складають функції Бесселя першого роду та другого роду [3], фундаментальну систему розв’язків для диференціального рівняння (Конторовича - Лєбєдєва) складають функції та [4].

Наявність фундаментальної системи розв’язків дозволяє будувати функції за правилами [2]

(6)

Умови спряження (3) для визначення п’яти невідомих та дають алгебраїчну систему із чотирьох рівнянь:

(7)

Алгебраїчна система (7) завжди сумісна [5].

При довільному розглянемо алгебраїчну систему стосовно та :

(8)

Визначник алгебраїчної системи (8)

Алгебраїчна система (8) має єдиний розв’язок:

(9)

При відомих вже розглянемо алгебраїчну систему стосовно :

(10)

Визначник алгебраїчної системи (10)

Алгебраїчна система (10) має єдиний розв’язок [5]:

(11)

У рівностях (11) беруть участь функції

,

.

Підставивши визначені величини та згідно формул (9) та (11) у рівності (6), маємо функції:

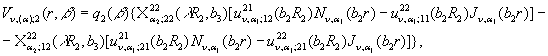
Отже, спектральна функція визначена.

Визначимо спектральну щільність

(13)

та вагову функцію

(14)

,

Наявність спектральної функції, вагової функції та спектральної щільності дає можливість визначити пряме та обернене гібридне інтегральне перетворення (ГІП), породжене на множині ГДО [6]:

, (15)

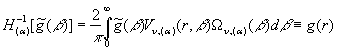(16)

Математичним обґрунтуванням правил (15), (16) є твердження

Теорема 1 (про інтегральне зображення). Якщо функція

обмежена, неперервна, абсолютно сумовна й має обмежену варіацію на множині , то для будь-якого має місце інтегральне зображення

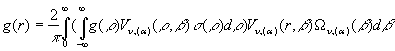(17)

Доведення. В основі доведення лежить подвійний невласний інтеграл

(18)

Припустимо тепер, що функція

(19)

Помножимо рівність (19) на вираз та проінтегруємо по

від до . В силу рівності (18) знаходимо:

Підставивши в (19) функцію ,

одержуємо інтегральне зображення (17).

Зауваження. Якщо кусково-неперервна, то зліва в (17) треба писати

.

Застосування запровадженого формулами (15), (16) ГІП до розв’язання відповідних задач базується на основній тотожності ГІП ГДО .

Теорема 2 (про основну тотожність). Якщо вектор-функція

неперервна на множині , а функції задовільняють умови обмеження

(20)

та умови спряження

(21)

то справджуються основна тотожність ГІП ГДО :

(22)

У рівності (22) прийняті позначення:

,

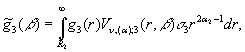
Доведення тотожності (22) проводиться стандартним методом [6].

Логічну схему застосування запровадженого формулами (15), (16) ГІП покажемо на одній з типових задач математичної фізики неоднорідних структур.

Задача квазістатистики. Знайти інтегральне зображення обмеженого в області розв’язку сепаратної системи диференціальних рівнянь параболічного типу [7]

(23)

за початковими умовами

(24)

та умовами спряження

(25)

Розв’язання. Запишемо систему (23) та початкові умови (24) в матричній формі:

(26)

Інтегральний оператор згідно правила (15) зобразимо у вигляді операторної матриці-рядка:

(27)

Застосуємо операторну матрицю-рядок (27) до системи (26) за правилом множення матриць. Внаслідок основної тотожності (22) отримуємо задачу Коші [2]:

(28)

Нехай . Покладемо ,, , .

Задача Коші (28) набуває вигляду:

,

(29)

Безпосередньо перевіряється, що розв’язом задачі Коші (29) є функція

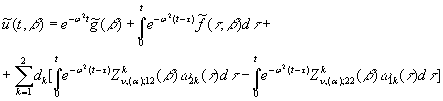(30)

Інтегральний оператор згідно правила (16) як обернений до (27) зобразимо у вигляді операторної матриці-стовпця:

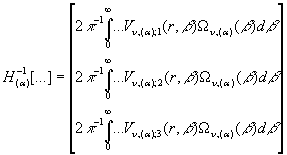(31)

Застосувавши за правилом множення матриць операторну матрицю-стовпець (31) до матриці-елементу , де функція визначена формулою (30), одержуємо інтегральне зображення єдиного розв’язку задачі квазістатистики (23) – (25):

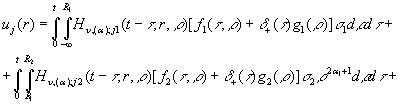
(32)

У рівності (32) беруть участь головні розв’язки параболічної задачі на спряження (23) - (25):

1) породжені неоднорідністю системи (23) функції впливу

, (33)

2) породжені неоднорідністю умов спряження функції Гріна

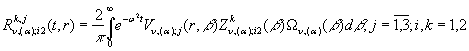, (34)

Зауважимо, що інтегральне зображення (32) аналітичного розв’язку даної задачі квазістатистики має алгоритмічний характер. Це дає можливість застосувати його як в теоретичних дослідженнях, так і в числових розрахунках. Більше того, структура головних розв’язків дозволяє вибором параметрів виділити будь-який практично потрібний випадок (в рамках даної моделі).

Література:

1. Шилов Г.Е. Математический анализ. Второй специальный курс.- М.: Наука, 1965.-328с.

2. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468с.

3. Ленюк М.П. Исследование основных краевых задач для диссипативного волнового уравнения Бесселя. – Киев, 1983. – 62с. – (Препринт / АН УССР. Ин-т математики; 83.3).

4. Ленюк М.П. Міхалевська Г.І. Інтегральні перетворення типу Конторовича – Лєбєдєва. – Чернівці: Прут, 2002. –280 с.

5. Курош А.Г. Курс высшей алгебры.- М.: Наука, 1971.-432с.

6. Ленюк М.П. Гібридні інтегральні перетворення типу Ейлера – (Фур’є, Бесселя).- Чернівці: Прут, 2009.-76с.

7. Тихонов А.Н., Самарський А.А. Уравнения математической физики. – М.: Наука, 1972. – 735с.

Ленюк Михайло Павлович вул. Головна 191, кв.15

м. Чернівці

Україна

58018

Тел. 0958589952