Ленюк М. П., Лусте І. П.
Чернівецький національний університет ім. Ю. Федьковича
ОБЧИСЛЕННЯ НЕВЛАСНИХ ІНТЕГРАЛІВ ЗА ВЛАСНИМИ ЕЛЕМЕНТАМИ ГІБРИДНОГО
ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА ЛЕЖАНДРА – (КОНТОРОВИЧА – ЛЄБЄДЄВА) – БЕССЕЛЯ
НА ПОЛЯРНІЙ ОСІ
Побудуємо на множині ![]() обмежений розв’язок сепаратної системи диференціальних рівнянь Лежандра
[1], (Конторовича - Лєбєдєва) [2] та Бесселя [3] для
модифікованих функцій
обмежений розв’язок сепаратної системи диференціальних рівнянь Лежандра
[1], (Конторовича - Лєбєдєва) [2] та Бесселя [3] для
модифікованих функцій
![]()
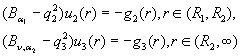 (1)
(1)
за умовами спряження
![]()
![]() (2)
(2)
Наявність фундаментальної
системи розв’язків дає можливість будувати розв’язок даної крайової задачі
методом функцій Коші [4,5]:
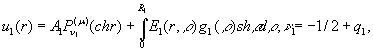

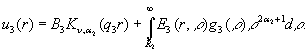 (3)
(3)
Тут ![]() - функції Коші
[4,5]:
- функції Коші
[4,5]:
 (4)
(4)
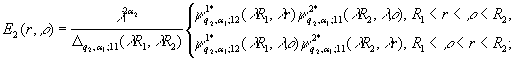 (5)
(5)
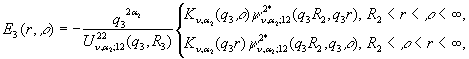 (6)
(6)
Нагадаємо, що ![]() ‑ узагальнений
диференціальний оператор Лежандра з особливою точкою
‑ узагальнений
диференціальний оператор Лежандра з особливою точкою ![]() ;
; ![]() ‑ диференціальний оператор Конторовича‑Лєбєдєва з
особливою точкою
‑ диференціальний оператор Конторовича‑Лєбєдєва з
особливою точкою ![]() [2];
[2]; ![]() ‑ диференціальний оператор
Бесселя з особливою точкою
‑ диференціальний оператор
Бесселя з особливою точкою ![]() [3].
[3].
Умови спряження (2) для
визначення величин ![]() дають неоднорідну
алгебраїчну систему з чотирьох рівнянь:
дають неоднорідну
алгебраїчну систему з чотирьох рівнянь:
![]()
![]() (7)
(7)
У системі (7) беруть участь функції
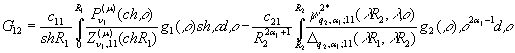
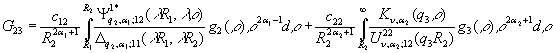
та символ Кронекера ![]() [6].
[6].
Введемо до розгляду
функції:
![]()
![]()
![]()
![]()
Припустимо, що виконана умова однозначної розв’язності крайової
задачі (1), (2): для будь-якого вектора ![]()
![]() визначник алгебраїчної
системи (7)
визначник алгебраїчної
системи (7)
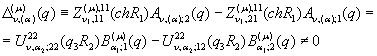 (8)
(8)
Визначимо головні розв‘язки крайової задачі (1) – (2):
1)
породжені неоднорідністю умов спряження функції Гріна
 ,
, 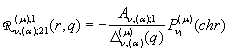 ,
,
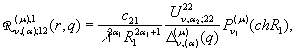
 ;
;
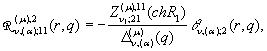
![]()
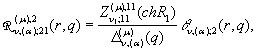 (9)
(9)
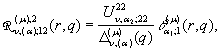
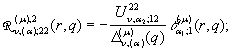
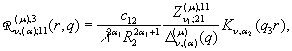


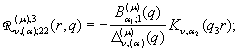
2)
породжені неоднорідністю
системи (1) функції впливу

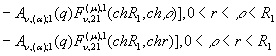
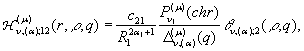
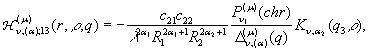
![]() (10)
(10)

![]()
![]()
![]()


У результаті однозначної
розв’язності алгебраїчної системи (7) та підстановки одержаних значень ![]() та
та ![]() у формули (3) маємо
єдиний розв’язок крайової задачі (1), (2):
у формули (3) маємо
єдиний розв’язок крайової задачі (1), (2):
 (11)
(11)
Побудуємо
розв’язок крайової задачі (1), (2) методом гібридного
інтегрального перетворення (ГІП), породженого на множині ![]() гібридним диференціальним оператором (ГДО)
гібридним диференціальним оператором (ГДО)
![]() (12)
(12)
Гібридний диференціальний оператор ![]() самоспряжений і має
одну особливу точку
самоспряжений і має
одну особливу точку ![]() . Тому його спектр дійсний та неперервний. Можна вважати, що
спектральний параметр
. Тому його спектр дійсний та неперервний. Можна вважати, що
спектральний параметр ![]() .Йому відповідає спектральна функція
.Йому відповідає спектральна функція
![]()
![]() ‑ одинична
функція Гевісайда [5].
‑ одинична
функція Гевісайда [5].
Функції ![]() задовільняють відповідно
диференціальні рівняння
задовільняють відповідно
диференціальні рівняння
![]()
![]() (13)
(13)
![]()
та умови спряження
![]() (14)
(14)
Якщо покласти [4]
![]()
![]() (15)
(15)
![]()
то умови спряження (14)
для визначення п’яти величин дають однорідну алгебраїчну систему із чотирьох
рівнянь:
 (16)
(16)
У результаті розв’язання
алгебраїчної системи (16), підстановки обчислених величин ![]() та
та ![]() у рівності (15) маємо
структуру функцій
у рівності (15) маємо
структуру функцій ![]() :
:
![]()
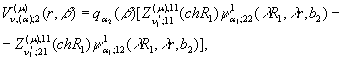 (17)
(17)
![]()
У рівності (17) прийняті
позначення:
![]()
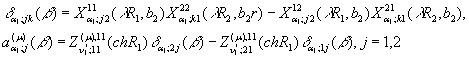
![]()
Визначимо числа
![]() ,
,
вагову
функцію
![]()
та спектральну щільність
![]() .
.
Наявність вогової функції ![]() , спектральної вектор-функції
, спектральної вектор-функції ![]() й спектральної щільності
й спектральної щільності ![]() дає можливість запровадити пряме
дає можливість запровадити пряме ![]() та обернене
та обернене ![]() ГІП типу Лежандра – (Конторовича -
Лєбєдєва) – Бесселя на полярній осі, породжене на множині
ГІП типу Лежандра – (Конторовича -
Лєбєдєва) – Бесселя на полярній осі, породжене на множині ![]() ГДО
ГДО ![]() [7]:
[7]:
 (18)
(18)
 , (19)
, (19)
вектор-функція ![]() з області визначення
ГДО
з області визначення
ГДО ![]() .
.
Введемо до розгляду величини та функції
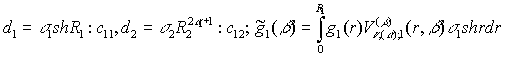 ,
,


![]()
В основі застосування ГІП ![]() до розв’язання відповідних задач знаходиться основна
тотожність ГІП ГДО
до розв’язання відповідних задач знаходиться основна
тотожність ГІП ГДО ![]() :
:
 (20)
(20)
Запишемо систему (1) в матричній формі:
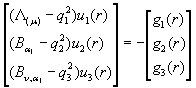 (21)
(21)
Інтегральний оператор ![]() згідно правила (18) зобразимо у
вигляді операторної матриці-рядка:
згідно правила (18) зобразимо у
вигляді операторної матриці-рядка:
 (22)
(22)
Нехай ![]() . Покладемо всюди
. Покладемо всюди ![]() . Застосуємо за правилом множення матриць операторну
матрицю-рядок (22) до системи (21).
Внаслідок тотожності (20) маємо алгебраїчне рівняння:
. Застосуємо за правилом множення матриць операторну
матрицю-рядок (22) до системи (21).
Внаслідок тотожності (20) маємо алгебраїчне рівняння:
![]()
Звідси знаходимо, що функція
![]() (23)
(23)
Інтегральний оператор ![]() згідно правила (19)
як обернений до (22) зобразимо у вигляді операторної матриці-стовпця:
згідно правила (19)
як обернений до (22) зобразимо у вигляді операторної матриці-стовпця:
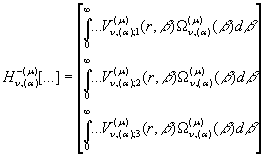 (24)
(24)
Застосуємо операторну матрицю-стовбець (24) за правилом
множення матриць до матриці-елементу ![]() , де функція
, де функція ![]() визначається формулою (23). Після
низки елементарних перетворень маємо єдиний розв’язок крайової задачі (1), (2):
визначається формулою (23). Після
низки елементарних перетворень маємо єдиний розв’язок крайової задачі (1), (2):
 (25)
(25)
![]()
Порівнюючи розв’язки (11) та (25) в силу єдиності, маємо
формули обчислення наступних невласних інтегралів:
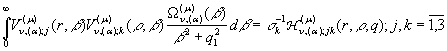 (26)
(26)
 (27)
(27)
 (28)
(28)
Функції впливу ![]() визначені за
формулами (10), а функції Гріна
визначені за
формулами (10), а функції Гріна ![]() умов спряження
визначені за формулами (9).
умов спряження
визначені за формулами (9).
Оскільки праві частини у формулах (26) – (28) не залежать від
нерівностей ![]() , то при необхідності можна покласти
, то при необхідності можна покласти ![]() .
.
Результатом дослідження є твердження.
Основна теорема. Якщо вектор-функція ![]()
неперервна на множині ![]() , функції
, функції ![]() задовільняють умови
обмеження
задовільняють умови
обмеження
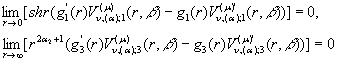
та умови спряження (2) й
виконується умова (8) однозначної розв’язності крайової задачі (1), (2), то є
вірними формулами (26) – (28) обчислення поліпараметричних невласних інтегралів
за власними елементами ГДО ![]() , визначеного рівністю (12)
, визначеного рівністю (12)
Література:
1.
Конет І.М., Ленюк М.П. Інтегральні перетворення типу Мелера – Фока. –
Чернівці: Прут, 2002. – 248с.
2.
Ленюк М.П. Міхалевська Г.І. Інтегральні перетворення типу Конторовича –
Лєбєдєва. – Чернівці: Прут, 2002. –280 с.
3.
Ленюк М.П. Исследование основных краевых
задач для диссипативного волнового уравнения Бесселя. – Киев, 1983. – 62с. –
(Препринт / АН УССР. Ин-т математики; 83.3).
4.
Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. –
468с.
5.
Шилов Г.Е. Математический анализ.
Второй специальный курс.- М.: Наука, 1965.-328с.
6.
Курош А.Г. Курс высшей алгебры.- М.: Наука, 1971.-432с.
Ленюк М.П., Янчишин М.Л. Гібридні інтегральні
перетворення типу (Фур’є – Конторовича - Лєбєдєва) – Лежандра. – Львів, 2002. –
76с. – (Препринт/НАН України.Ін-т прикладних проблем механіки і математики ім.
Я.С. Підстригача; 01.02). – Чернівці: Прут, 2002. – 76с.