Веренич І.І., Ленюк М.П.
Національний
технічний університет „ХПІ”
ОБЧИСЛЕННЯ НЕВЛАСНИХ ІНТЕГРАЛІВ ЗА ВЛАСНИМИ ЕЛЕМЕНТАМИ ГІБРИДНОГО
ДИФЕРЕНЦІАЛЬНОГО ОПЕРАТОРА БЕССЕЛЯ – (КОНТОРОВИЧА - ЛЄБЄДЄВА) – ЛЕЖАНДРА НА
ПОЛЯРНІЙ ОСІ ![]()
Побудуємо обмежений на множині
![]()
розв’язок сепаратної системи диференціальних рівнянь Бесселя [1], Конторовича – Лєбєдєва [2] та Лежандра [3] для модифікованих
функцій
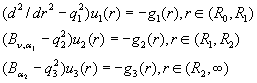 (1)
(1)
за крайовими мовами
![]() ,
, ![]() (2)
(2)
та умовами спряження
![]() (3)
(3)
У рівностях (1) бере участь диференціальні
оператори Фур’є ![]() [1], Бесселя
[1], Бесселя ![]() , [2] та диференціальний оператор (Конторовича - Лєбєдєва)
, [2] та диференціальний оператор (Конторовича - Лєбєдєва) ![]() [3];
[3]; ![]() ,
, ![]() .
.
Вважаємо,
що виконані умови на коефіцієнти:

Фундаментальну систему розв’язків
для диференціального рівняння Фур’є ![]() складають функції
складають функції ![]() та
та ![]() [1]; фундаментальну систему розв’язків для
диференціального рівняння Бесселя
[1]; фундаментальну систему розв’язків для
диференціального рівняння Бесселя ![]() склаутворюють функції Це дозволяє розв’язок крайової
задачі (1) - (3) будувати методом функцій Коші [1]:
склаутворюють функції Це дозволяє розв’язок крайової
задачі (1) - (3) будувати методом функцій Коші [1]:
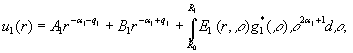
 (4)
(4)
У рівностях (4) ![]() ,
,![]() функція Коші [1]:
функція Коші [1]:
![]()
 (5) Припустимо, що
функція Коші
(5) Припустимо, що
функція Коші

Властивості (5) функції Коші
дають алгебраїчну систему з двох рівнянь:
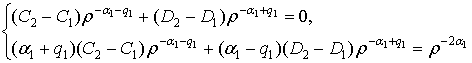
Звідси знаходимо співвідношення:
![]() (6)
(6)
Доповнимо рівності (6) алгебраїчними рівнянням:
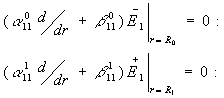
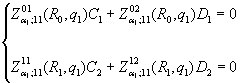
![]() (7)
(7)
Алгебраїчна система (7) внаслідок співвідношень
(6) набуває вигляду:
 (8)
(8)
Із алгебраїчної системи (8)знаходимо, що
![]()
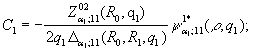
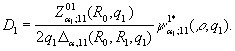
Цим функція Коші ![]() визначена й в силу
симетрії відносно діагоналі
визначена й в силу
симетрії відносно діагоналі ![]() має структуру:
має структуру:
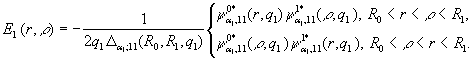 (9)
(9)
В рівностях (7) - (9) прийняті позначення:
![]() ,
,
![]() ,
,
![]()
![]()
Припустимо, що функція Коші

Властивості (5) функції Коші дають співвідношення:
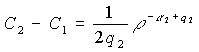 ,
, ![]()
![]() (10)
(10)
Доповнимо алгебраїчними рівняннями:
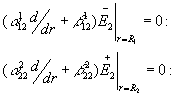
 (11)
(11)
Система (11) внаслідок
рівностей (10) набуває вигляду:
![]()
![]()
Звідси
знаходимо, що


Цим
функція Коші ![]() визначена й внаслідок
симетрії відносно діагоналі
визначена й внаслідок
симетрії відносно діагоналі ![]() має структуру:
має структуру:
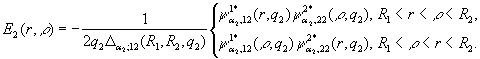 (12)
(12)
Тут беруть участь функції:
![]()
![]() .
.
Крайові умови (2) та умови спряження (3) для визначення
чотирьох величин ![]() дають алгебраїчну
систему з чотирьох рівнянь:
дають алгебраїчну
систему з чотирьох рівнянь:
![]() ,
,
![]() ,
,
![]() (13)
(13)
.
У системі (13) бере участь
функція
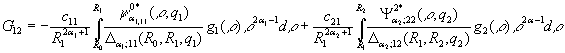 .
.
та символ Кронекера ![]() [2].
[2].
Припустимо, що виконана умова однозначної розв’язності крайової
задачі (1) - (3): для будь-якого ненульового вектора ![]() ={q1;
={q1; ![]() } визначник алгебраїчної системи (13) відмінний від нуля [2]:
} визначник алгебраїчної системи (13) відмінний від нуля [2]:
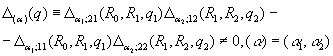 (14)
(14)
Визначимо головні розв‘язки крайової задачі (1) – (3):
1) породжені крайовою
умовою в точці ![]() функції Гріна
функції Гріна
![]() ,
, ![]() ;
; ![]() (15)
(15)
2) породжені крайовою умовою в точці ![]() функції Гріна
функції Гріна
![]() (16)
(16)
![]()
3) породжені неоднорідністю умов спряження функції Гріна
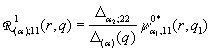 ,
,  ,
,
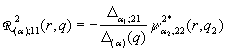 ,
,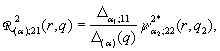 (17)
(17)
4) породжені неоднорідністю системи функції впливу

![]() (18)
(18)
![]() ,
,
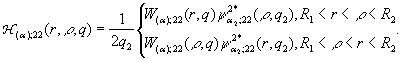
У результаті
однозначної розв’язності алгебраїчної системи (13) та
підстановки обчислених значень величин ![]() у формули (4) маємо
єдиний розв’язок крайової задачі (1) – (3):
у формули (4) маємо
єдиний розв’язок крайової задачі (1) – (3):
![]()
 . (19)
. (19)
Побудуємо
тепер розв’язок крайової задачі методом інтегрального перетворення, породженого на
множині ![]() диференціальним оператором
диференціальним оператором
![]() ,
, ![]() . (20)
. (20)
Диференціальний оператор ![]() самоспряжений і на
множині
самоспряжений і на
множині ![]() не має особливих
точок. Отже, його спектр дійсний та дискретний [3].
Йому відповідає дійсна спектральна функція
не має особливих
точок. Отже, його спектр дійсний та дискретний [3].
Йому відповідає дійсна спектральна функція
![]() , (21)
, (21)
де ![]() –спектральний параметр.
–спектральний параметр.
Для знаходження власних
елементів (спектра й спектральної функції) оператора ![]() розглянемо
спектральну задачу Штурма - Ліувілля: знайти ненульовий розв’язок однорідної
системи
розглянемо
спектральну задачу Штурма - Ліувілля: знайти ненульовий розв’язок однорідної
системи
![]()
![]()
![]()
![]() (21)
(21)
за однорідними крайовими умовами
(2) та однорідними умовами спряження (3): (![]() );
); ![]() ,
, ![]() ,
, ![]()
Фундаментальну систему розв’язків для диференціального
рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1].
[1].
Якщо покласти
![]() ,
,
![]() , (22)
, (22)
то однорідні крайові умови та однорідні умови спряження
для визначення величин ![]() дають однорідну алгебраїчну систему з чотирьох рівнянь:
дають однорідну алгебраїчну систему з чотирьох рівнянь:
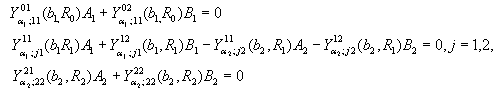 (23)
(23)
У системі (23) прийняті
позначення:
![]() ,
,
![]() .
.
Введемо до розгляду функції:
![]() ;
;
![]() .
.
Алгебраїчна система має ненульові розв’язки
тоді й тільки тоді, коли її визначник рівний нулю [2]:
![]() (24)
(24)
Ми одержали трансцендентне рівняння для обчислення
власних чисел диференціального оператора ![]() .
.
Підставимо корінь ![]() рівняння (24) в
систему (23) й відкинемо останнє рівняння в силу лінійної залежності. Покладемо
рівняння (24) в
систему (23) й відкинемо останнє рівняння в силу лінійної залежності. Покладемо
![]()
![]() ,
, ![]()
Відносно ![]() отримуємо алгебраїчну
систему
отримуємо алгебраїчну
систему
![]() . (25)
. (25)
Визначник алгебраїчної системи (25)
![]()
Алгебраїчна система (25)
має єдиний розв’язок [2]:
![]() ,
, ![]() ,
, ![]() ;
;
![]() ,
, ![]()
Підставивши визначені
величини ![]() у рівності (22),
маємо функції:
у рівності (22),
маємо функції:
![]() ,
,
![]() . (26)
. (26)
Спектральна вектор-функція ![]() визначена.
визначена.
Визначимо числа
![]() ,
, ![]() ,
,
вагову
функцію
![]() , та квадрат норми власної (спектральної) функції
, та квадрат норми власної (спектральної) функції
 .
.
Наявність спектральної функції з її
квадратом норми та вагової функції дозволяє визначити скінченне інтегральне
перетворення, породжене на множині ![]() оператором
оператором ![]() [3]:
[3]:
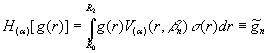 , (27)
, (27)
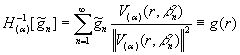 (28)
(28)
Введемо
до розгляду величини та функції:
![]() ,
, 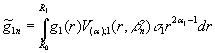 ,
, 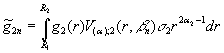 ;
;
![]()
Має місце основна
тотожність [3]:
![]()
![]() (29)
(29)
Єдиний розв’язок крайової
задачі (1)-(3) одержаний за відомою логічною схемою методом запровадженого
формулами (27)-(29) скінченного інтегрального перетворення [3], має структуру:
 +
+
+  +
+
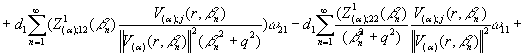
 j=1,2 (30)
j=1,2 (30)
Порівнюючи розв‘язки (19) та (30) в силу
єдиності, приходимо до таких формул підсумовування функціональних рядів:
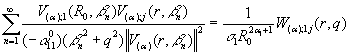 , j = 1, 2 (31)
, j = 1, 2 (31)
 , j = 1, 2 (32)
, j = 1, 2 (32)
 , j = 1, 2 (33)
, j = 1, 2 (33)
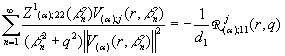 , j = 1, 2 (34)
, j = 1, 2 (34)
 , j,к = 1, 2 (35)
, j,к = 1, 2 (35)
Тут ![]() .
.
Підсумком наведеного в даній роботі дослідження є
твердження.
Основна теорема: Якщо вектор-функція ![]() неперервна на множині
неперервна на множині
![]() , функції
, функції ![]() задовольняють крайові
умови (2) та умови спряження (3) і виконується умова (14) однозначної
розв’язності крайової задачі (1) - (3), то справджуються формули (31) - (35)
підсумовування функціональних рядів за власними елементами диференціального
оператора Ейлера
задовольняють крайові
умови (2) та умови спряження (3) і виконується умова (14) однозначної
розв’язності крайової задачі (1) - (3), то справджуються формули (31) - (35)
підсумовування функціональних рядів за власними елементами диференціального
оператора Ейлера ![]() , визначеного рівністю (20).
, визначеного рівністю (20).
Література:
1.Степанов В.В. Курс дифференциальных уравнений. - М.:Физматгиз,
1959.-468с.
2. Курош А.Г. Курс высшей алгебры.- М.: Наука, 1971.-432с.
3. Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні
інтегральні перетворення, породжені
диференціальними рівняннями друго порядку. – Чернівці: Прут, 2001.-
228с.