Сизоненко
В.Л., Масленников Д.И.
Харьковский национальный аграрный университет
имени
В.В.Докучаева
Токовая бунемановская неустойчивость
в замагниченной плазме
В 70-80-тые годы прошлого века неустойчивости плазмы с
током,
текущим вдоль внешнего
магнитного поля ![]() , исследовались чрезвычайно
, исследовались чрезвычайно
интенсивно [1] – [10], потому
что казалось: стоит только ввести в плазму
извне большую энергию и
осуществление управляемого термоядерного
синтеза будет обеспечено. И
только значительно позже стало ясно, что нужно
еще и удержать в плазме эту
энергию вместе с удержанием частиц, что
представляет задачу намного
более сложную. Тем не менее, способ
предварительного нагрева
плазмы с помощью токовой бунемановской
неустойчивости до сих пор
применяется в Токаманах и других пламенных
ловушках как один из весьма
надежных.
В ХХ1 веке интерес к этой проблеме возродился в связи с
появлением
новой теории описания
возбуждения микронеустойчивостей плазмы [11] –
[13], которая оказалась
намного проще существующих теорий и приводила к
конечному результату раньше, чем в плазме разовьются так
называемые
модуляционные неустойчивости [14].
В работе [15] исследовалась первая
стадия бунемановской
неустойчивости и было показано, что поток
электронной плазмы теряет
примерно половину своей начальной токовой
скорости ![]()
Для описания дальнейшего
процесса торможение потока электронов
требуется учитывать не только
Черенковское взаимодействия волн и частиц ![]() , но и электронные циклотронные резонансы
, но и электронные циклотронные резонансы ![]() где
где![]() - электронная циклотронная частота,
- электронная циклотронная частота, ![]() и
и ![]() - заряд и масса
электрона.
- заряд и масса
электрона.
Механизм стохастического нагрева частиц в случае
бунемановской
неустойчивости плазмы без
магнитного поля был исследован в работе [12], в
которой обнаружено сильное
торможение потока электронов с переходом
почти половины их
кинетической энергии в температуру этих частиц.
В данной работе мы продолжим исследование нелинейной
стадии
возбуждения бунемановской
неустойчивости в замагниченной плазме
-
1 -
начатое в работе[15]. Будем
предполагать что электрические поля колебаний![]() создаются разделенными в пространстве волновыми
создаются разделенными в пространстве волновыми
пакетами, проходя которые частицы плазмы получают случайные
приращения скоростей ![]() ( «толчки») ( см.[11]
– [16]).
( «толчки») ( см.[11]
– [16]).
В работе [14] показано, что в магнитоактивной плазме
система нелинейных уравнений для средних скоростей электронов ![]() и ионов
и ионов ![]() вдоль внешнего
магнитного поля
вдоль внешнего
магнитного поля ![]() и для среднеквадратических флуктуаций скоростей
и для среднеквадратических флуктуаций скоростей ![]() и
и ![]() в отличие от [12]
имеет следующий вид:
в отличие от [12]
имеет следующий вид:
 , (1)
, (1)
 (2)
(2)
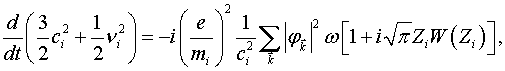 (3)
(3)
 (4)
(4)
где ![]() массы электронов,
ионов,
массы электронов,
ионов, ![]() Фурье-компонента потенциала
Фурье-компонента потенциала ![]() с волновым вектором
с волновым вектором ![]() и
и  продольная и
поперечная составляющая вектора
продольная и
поперечная составляющая вектора ![]() относительно магнитного поля
относительно магнитного поля ![]() комплексная частота, состоящая из реальной
комплексная частота, состоящая из реальной ![]() и мнимой
и мнимой ![]() частей,
частей,
- 2
-
![]() функция Крампа:
функция Крампа:
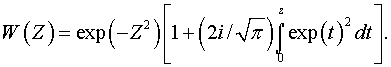
При выводе уравнений (1) - (4) предполагалось, что
ионы незамагничены ![]() , а электроны достаточно холодные
, а электроны достаточно холодные ![]() . Их поперечная энергия
. Их поперечная энергия ![]() предполагалась малой
предполагалась малой
так![]() что для
что для ![]() справедливо уравнение
справедливо уравнение
 (5)
(5)
Напоминаем, что 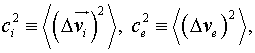 где
где ![]() и
и ![]() приращения скоростей
ионов и электронов (вдоль магнитного поля) при их многократных рассеяниях на волновых
пакетах со случайными фазами, а символ
приращения скоростей
ионов и электронов (вдоль магнитного поля) при их многократных рассеяниях на волновых
пакетах со случайными фазами, а символ ![]() означает усреднение
по всему объему плазмы или по нормальным распределениям этих величин [12] -
[14]. Фактически
означает усреднение
по всему объему плазмы или по нормальным распределениям этих величин [12] -
[14]. Фактически ![]() температура ионов плазмы, а
температура ионов плазмы, а ![]() продольная температура электронов.
продольная температура электронов.
Кроме (1) – (5) имеет место дисперсионное уравнение
для волн
![]() (6)
(6)
-
3 -
где

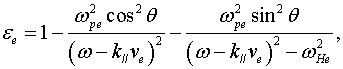
![]() плотность частиц
плазмы,
плотность частиц
плазмы, ![]() угол между
угол между ![]() и
и ![]()
В случае ![]() уравнение (6)
переходит в известное дисперсионное уравнение линейной теории [6], [10]
уравнение (6)
переходит в известное дисперсионное уравнение линейной теории [6], [10]
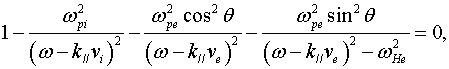 (7)
(7)
в котором скорости ![]() и
и ![]() изменяются согласно уравнениям (1), (2).
изменяются согласно уравнениям (1), (2).
Отбрасывая в (7) второе слагаемое и полагая ![]() в третьем и
четвертом, найдем те значения
в третьем и
четвертом, найдем те значения ![]() , при которых волны нарастают наиболее быстро:
, при которых волны нарастают наиболее быстро:
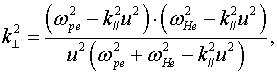 (8)
(8)
где ![]() . Удерживая теперь отброшенные члены, получим частоту
. Удерживая теперь отброшенные члены, получим частоту ![]() и инкремент
и инкремент ![]() колебаний:
колебаний:
![]() (9)
(9)
где ![]()
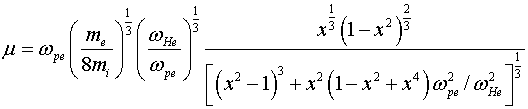 .
.
- 4 -
Из (8), (9) следует, что при ![]() возбуждаются волны с
возбуждаются волны с
![]() (10)
(10)
для которых по порядку величины справедливы оценки
[6]:
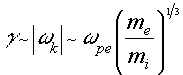 (11)
(11)
При этом из (1) – (5) нетрудно получить, что ![]()
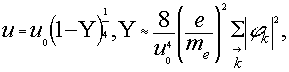 (12)
(12)
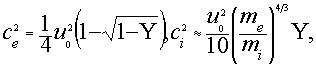 (13)
(13)
![]() (14)
(14)
где ![]() и
и ![]() - начальные (при
- начальные (при ![]() ) скорость электронов и их поперечная тепловая скорость
соответственно. Аналогично, для величин
) скорость электронов и их поперечная тепловая скорость
соответственно. Аналогично, для величин ![]() и
и ![]() при выполнении
условий (11) – (14) справедливы оценки
при выполнении
условий (11) – (14) справедливы оценки
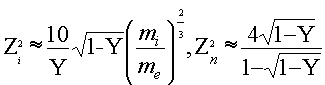 (15)
(15)
Из (15) следует, что при ![]() соотношения (10) –
(14) справедливы, и наблюдается сильное торможение электронного потока вплоть
до значений
соотношения (10) –
(14) справедливы, и наблюдается сильное торможение электронного потока вплоть
до значений
![]() (16)
(16)
При этом поперечная энергия электронов остается малой.
- 5
-
В случае