Новый метод аналитической аппроксимации функции Хевисайда

Д.т.н. Алюков С.В., асп. Алюков А.С.

Южно-Уральский государственный университет,

Челябинск, Россия

Функция Хевисайда (функция единичного скачка) является одной из основополагающих функций в математике и широко применяется, например, в теории автоматического управления, передачи сигналов при описании переходных процессов из одного состояния исследуемой системы в другое [1,2] и во многих других областях фундаментальных и прикладных исследований. Эта функция является кусочно-постоянной, в нуле она, вообще говоря, не определена, но, как правило, ее доопределяют в нуле некоторым числом, обычно равным 0,5 [3]:

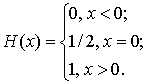
Однако, разрыв функции в нуле часто препятствует применению аналитических методов в проводимых исследованиях, так как приходится рассматривать системы переменной структуры, разбивать исследуемые процессы на участки с дальнейшим "сшиванием" полученных по участкам решений. При этом возникают трудности с изучением процессов в течение цикла, построением периодических решений, определением их устойчивости. Кроме того, кусочно-линейные разрывные функции, включая функцию Хевисайда, недостаточно точно соответствуют реальным процессам, так как на практике мгновенный скачок значений параметров реальных процессов невозможен. Так, например, мгновенное изменение значение скорости материальной точки или механической системы требует бесконечной энергии.

На практике для преодоления отмеченных трудностей прибегают к аппроксимации функции Хевисайда аналитическими функциями. В качестве таких аппроксимаций могут выступать, например, такие функции, как:

при достаточно больших значениях параметра .

Возможны и другие методы аппроксимации функции Хевисайда [4].

В данной статье предлагается новый метод аппроксимации функции Хевисайда аналитической зависимостью. В качестве аппроксимирующей функции предлагается взять функцию вида:

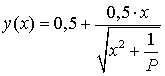
при достаточно большом значении параметра .

На рис. 1 изображены графики аппроксимаций функции Хевисайда аналитическими функциями при одном и том же значении параметра . Сплошной линией изображен график предложенной аппроксимации, пунктирной линией – аппроксимирующей функции, включающей экспоненту, точечной линией – аппроксимации, выраженной через обратную тригонометрическую функцию .

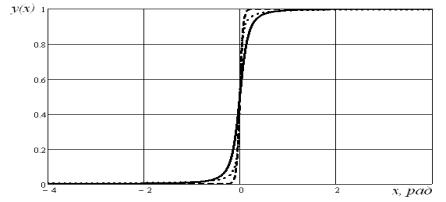
Рис.1. Графики аналитических аппроксимаций функции Хевисайда

Сравнительный анализ графиков (рис.1) показывает, что функция с экспонентой наилучшим образом приближает функцию Хевисайда. Что же касается остальных двух рассматриваемых аппроксимаций, то можно отметить, что аппроксимация с обратной тригонометрической функцией лучше приближает функцию Хевисайда в окрестности точки разрыва, но хуже, чем предложенная функция, приближает функцию Хевисайда внутри промежутков ее постоянства. Так на рис. 2 изображены графики рассмотренных аппроксимирующих функций на промежутке [1; 2,5]. Здесь опять, сплошной линией изображен график предложенной аппроксимации, пунктирной линией – аппроксимирующей функции, включающей экспоненту, точечной линией – аппроксимации, выраженной через обратную тригонометрическую функцию . Данные графики наглядно подтверждают сделанные утверждения.

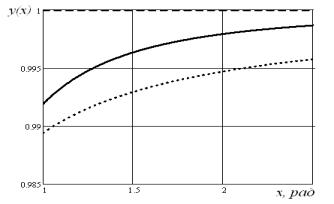
Рис.2. Графики аналитических приближений функции Хевисайда

внутри промежутков ее постоянства

Возвращаясь к рис. 1, заметим, что предложенный метод аппроксимации может оказаться наиболее приемлемым для аппроксимации функции Хевисайда в исследованиях реальных процессов, так как в наилучшей степени сглаживает угловые участки протекания этих процессов.

Литература

1. Ким Д.П. Теория автоматического управления (в 2-х томах), М.: ФИЗМАТЛИТ, 2003, 2004, 288 +464 с.

2. Игнатов В.А. Теория информации и передачи сигналов: Учебник для ВУЗов, М.: Советское радио, 1979, 280 с.

3. Корн Г., Корн Т. Справочник по математике (для научных работников и инженеров), М.: 1977, 831 с.

4. Алюков С.В. Аппроксимации кусочно-линейных и обобщенных функций, Германия: LAP LAMBERT Academic Publishing GmbH&Co. KG., ISBN: 978-3-8484-9048-6, 2012, 120 с.