Сизоненко
В.Л., Коваленко Н.И.
Харьковский национальный аграрный университет имени В.В. Докучаева
К плазменной модели распространения нервного импульса
После выхода в свет работ Ходжкина и
Хаксли [1], [2] прошла буквально лавина исследований механизма распространения
нервного импульса в биологически активной мембране (см. [3] – [6] и
цитированную там литературу). В частности, существенное развитие теории этого
явления принадлежит работам Маркина, Чизмаджева и др. авторов, выполненных в
1969–1974 гг. [4, с.373], [5]. Они, по-существу, стали классическими в области
нейробиологии.
В основу теоретических работ было положено
уравнение распространения возбуждения по немиелизированному однородному волокну
мембраны [4, с.373]:
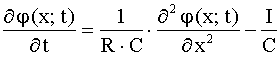, (1)
где 
– потенциал мембраны,
отсчитываемый от потенциала покоя, 
– сумма внешнего и
внутреннего сопротивлений, 
– емкость единицы
длины волокна, 
– ионный ток, текущий
через мембрану (отнесенный к единице длины волокна); 
> 0, если ток
течет наружу.
Если импульс бежит по волокну с постоянной
скоростью 
, то уравнение (1), переписанное в терминах переменной 
, принимает вид [4]:
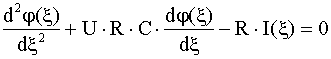, (2)
где выполнены условия: 
и 
. Оказалось, что прямая 
= 18,5 мВ пересекает
кривую 
в двух точках,
соответствующих большей (
) и меньшей (
) скорости 
, но одно из решений (
) неустойчиво. Эта теория показала, что скорость
распространения импульса определяется электрическими и геометрическими
параметрами аксона, практические независимо от формы исходного импульса [4].
Вместе с тем, уравнение (1) является
феноменологическим, выведенным на основании некой электрической схемы мембраны,
и поэтому может не отражать всех тонкостей протекания тока по аксоплазме. В настоящей работе мы развили теорию
протекания токов в цитоплазме аксона и вне го, рассматривая жидкости с обеих
сторон мембраны как электролиты, содержащие плазму ионов разных сортов. В итоге
нами получены уравнения типа (1), (2), но отличающиеся от них в некоторых
деталях.
Будем считать условно, что биологическая
мембрана лежит параллельно оси 
в области 
и бесконечна вдоль 
. С наружной стороны мембраны (
) присутствует электролит, в котором имеются однозарядные
ионы 
, 
и 
, коэффициенты диффузии которых 
одинаковы (в действительности они одного порядка):
(
) ~ 
(
) ~ 
(
) ~ 
см2/с, но
для расчетов это не имеет принципиального значения). В цитоплазме аксона (
) находится такой же электролит с ионами 
, 
и 
, но здесь еще содержится и значительная часть анионов 
органического происхождения (изэтионовая кислота) [4, с.365],
которые сквозь тело липидного бислоя мембраны проникать не могут. Наличием
двухзарядных ионов 
, 
и др. пренебрегаем.
Для определения распределения потенциала 
электрического поля 
в электролите необходимо решить систему уравнений для плотностей
частиц 
ионы 
; 
; 
; 
).
, (3)
, (4)
где
и 
– электрический заряд иона 
, 
– температура, 
– диэлектрическая проницаемость среды (
≈ 80, как и для воды). Плотности потоков зарядов 
определяются
соотношениями
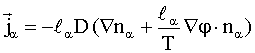, (5)
При этом задаются следующие граничные
условия:
|
|
(6) |
Если учесть, что перенос частиц из-за
диффузии в электролите происходит за характерные времена
~ 
~ 
~ 
, (7)
которые значительно меньше времени
прохождения нервного импульса (~
), то левые части в (3) малы, и для 
справедливы выражения
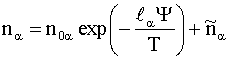, (8)
где
, 
при 
, 
при 
. В области, где 
, из (3) находим, что
, (9)
где
– плотность тока (5)
вдоль оси 
на поверхности
мембраны 
; 
при 
, 
при 
. При выводе соотношений (8), (9) предполагалось, что 
, 
.
Уравнение
(4) с учетом (8) в области 
следующее:
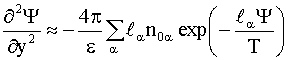. (10)
В случае 
решения уравнения
(10) имеют вид:
; 
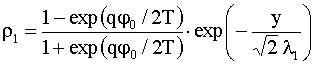, (11)
а при 
они заданы
соотношением:
; 
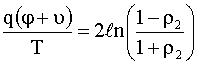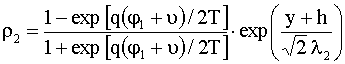, (12)
где
и 
– значения потенциала
на границах мембраны 
и 
соответственно:
, 
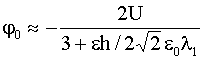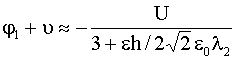, (13)
– радиус Дебая-Гюхкеля в области 
, 
– его значение при 
, 
– диэлектрическая
проницаемость липидного бислоя. При получении соотношений (13) предполагалось,
что 
, но ими можно пользоваться и в случае 
~ 
.
На начальной стадии нервного импульса,
когда открываются натриевые каналы, и ионы 
начинают входить
внутрь аксона, можно считать, что в наружной среде 
, 
, а ионы калия и анионы 
отсутствуют 
. Тогда из уравнения (9) с учетом (11) получим, что 
, 
,
|
|
(14) |
Если выполнено условие
, (15)
то из (14) следует, что в области 
плотность 
становится исчезающее
малой 
, и ток ионов натрия отсутствует.
Поскольку ионы хлора (
) не могут проходить через мембрану, то они с уходом ионов
натрия начинают перемещаться в область больших положительных значений 
. При этом в интервале 
из (9) получаем, что
|
|
(16) |
.В области 
плотность 
возрастает с ростом 
, достигая при 
~ 
максимальной величины, которая остается значительно меньшей 
. Здесь же, согласно (4), появляется и маленькое
электрическое поле, которое для наших расчетов не имеет значения. Иными
словами, излишние ионы хлора уходят от поверхности мембраны во внешнюю область,
так что максимум их плотности находится в точке 
~ 
.
При поступлении ионов натрия во внутреннюю
область аксона уравнения (8), (9) для 
здесь неприменимы,
поскольку на какое-то время (порядка 
~ 
) плотность этих ионов может
стать больше исходной равновесной 
. Однако, при больших временах 
излишние ионы 
уходят от поверхности
мембраны во внутреннюю часть аксона, так что их плотность 
вблизи липидного
бислоя опять становится малой, и на распределение потенциала вдоль 
не влияет.
Рассмотрим теперь поведение ионов во
внутренней аксоплазме на второй стадии процесса, когда натриевые каналы
мембраны закрываются, но открываются каналы для ионов 
. Тогда 
, 
, 
, 
, и для 
становятся
справедливыми соотношения типа (8), (9):
= 
, 
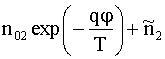, (17)
(18)
Подставляя в (18) выражение (12) для 
, получим аналогично (14), (15) следующие формулы:
,
|
|
(19) |
.Если выполнено условие
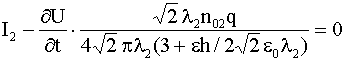, (20)
то из (19) следует, что в области 
плотность 
становится исчезающее
малой 
, и ток ионов калия отсутствует.
Поскольку анионы 
не могут проходить
через мембрану, то они с уходом ионов калия начинают перемещаться в область
больших отрицательных значений 
. При этом в интервале 
из (9) получаем, что
|
|
(21) |
.В области 
плотность 
возрастает с
уменьшением 
, достигая при 
~ 
максимальной
величины, которая остается значительно меньшей 
. Здесь же, согласно
(4), возникает и маленькое электрическое поле, которое для наших расчетов не
имеет значения. Иными словами, излишние анионы 
уходят от поверхности
мембраны внутрь аксона, так что максимум их плотности находится в точке 
~ 
(
– момент времени,
когда 
).
При поступлении ионов калия во внешнюю
область аксона уравнения (8), (9) для 
здесь неприменимы,
поскольку на какое-то время (порядка 
) плотность этих ионов может стать больше исходной
равновесной 
. Однако, при больших
временах (
) излишние ионы 
уходят от поверхности
мембраны во внешнюю часть аксона, так что их плотность 
вблизи липидного
бислоя опять становится малой, и на распределение потенциала вдоль 
не влияет.
Основную ценность для нас представляют соотношения
(15) и (20), поскольку они связывают ток через мембрану с изменением потенциала
. Полагая далее, что
|
I = |
|
(22) |
|
|
,
,
, 
, (23)
приходим к следующей формуле связи тока 
с потенциалом 
:
|
|
при |
(24) |
|
|
при |
,
,
.Сравним теперь формулы (24) с (2). Видно,
что у нас первые слагаемое в (2) отсутствует, а для емкости 
справедлива оценка
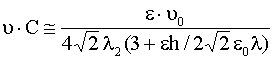. (25)
Прежде, чем сравнивать наши результаты с
экспериментами, отметим, что развитая здесь теория пригодна только для
немиелизированных аксонов, так как мы не предполагали наличие перехватов Ранвье
во внешней области аксона. Как известно, скорости распространения импульсов в
таких системах лежат в пределах 
= 0,7 – 2,3 м/с, в то
время как в миелизированных волокнах
они равны: 
= 10–100 м/с [4, c.361]. Беря теперь значения: 
~ 1019 см-3, 
30 нм, 
= 50 нм, 
80, 
4, 
= 20 м/с, 
= 1,5 м/с, получим из
(25), что
~ 
ед. 
= 0,2 мкΦ/см. (26)
Эта оценка хорошо соответствует значению 
= 0,157 мкΦ/см,
найденному для аксонов [4, c.373].
Нашей моделью можно пользоваться, однако,
и в случае миелизированных волокон, если под током 
подразумевать
значение тока, усредненное по некоторой длине, содержащей несколько перехватов
Ранвье. При этом нужно учитывать, что в немиелизированном аксоне через 1 мкм2
поверхности проходит около 20 000 ионов 
, так что плотность ионного тока в перехвате примерно в
десять раз больше, чем в немиелизированных гигантских аксонах [4, c.368]. Поэтому для применимости нашей модели ток 
в (24) должен быть
уменьшен приблизительно в десять раз, что эквивалентно увеличению значение 
тоже в десять раз,
т.е. до предела 
10
15 м/с. В этом случае опять получаем для 
оценку (26).
Уменьшение коэффициента при 
во второй формуле
(24) почти в два раза, казалось бы, должно увеличивать крутизну фронта
потенциала 
. В действительности же этого не происходит по той причине,
что ток ионов калия возрастает намного медленнее, чем входной ток ионов натрия.
Развитая нами теория, основанная на
решении точных уравнений диффузии ионов в электрометах, показывает, что первое
слагаемое в (2) привнесено туда искусственно. Однако, без него далеко идущие
выводы о поведении нервных импульсов в аксонах [4], [7], оказываются
недоказанными.
Литература:
1.
Hodgkin A.L., Huxley A.F. // I. Physiol. 1952. V. 117. P. 500–544.
2.
Ходжкин А. Нервный
импульс: Пер. с англ. М.: Мир, 1965.
3.
Шеперд Г. Нейробиология.
Т. 1: Пер. с англ. М.: Мир, 1987. – 454 с.
4.
Волькенштейн М.В.
Биофизика. М.: Наука, 1988. – 592 с.
5.
Ходоров Б.И. Общая
биология возбудимых мембран. М.: Наука, 1975.
6.
Тасаки Н. Нервное
возбуждение: Пер. с англ. М.: Мир, 1971.
7.
Маркин В.С., Пастушенко
В.Ф., Чизмаджев Ю.А. Теория возбудимых сред. М.: Наука, 1981
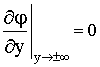
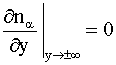
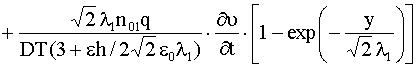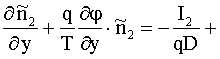
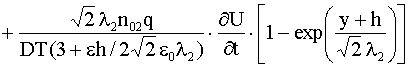
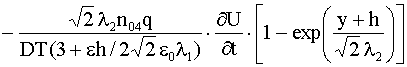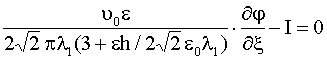