Катело Я.Д.
Донецький Національний Університет Економіки і Торгівлі
імені Михайла Туган – Барановського,Україна
ПРОБЛЕМЫ ПРИМЕНЕНИЯ МАТЕМАТИЧЕСКИХ
МЕТОДОВ В ЭКОНОМИКЕ
Невозможно представить себе современную науку без широкого применения математического моделирования. Сущность этой
методологии состоит в замене исходного объекта его "образом" —
математической моделью — и дальнейшем изучении модели с помощью реализуемых на
компьютерах вычислительно-логических алгоритмов. Этот "третий метод"
познания, конструирования, проектирования сочетает в себе многие достоинства
как теории, так и эксперимента. Работа не с самим объектом (явлением, процессом), а с его моделью дает возможность
безболезненно, относительно быстро и без существенных затрат исследовать
его свойства и поведение в любых мыслимых ситуациях (преимущества теории). В то
же время вычислительные (компьютерные, симуляционные, имитационные)
эксперименты с моделями объектов позволяют, опираясь на мощь современных вычислительных
методов и технических инструментов информатики, подробно и глубоко изучать
объекты в достаточной полноте, недоступной чисто теоретическим подходам
(преимущества эксперимента). Неудивительно, что методология математического
моделирования бурно развивается, охватывая
все новые сферы - от разработки технических систем и управления ими до
анализа сложнейших экономических и социальных процессов.Элементы
математического моделирования использовались с самого начала появления точных
наук, и не случайно, что некоторые методы вычислений носят имена таких корифеев
науки, как Ньютон и Эйлер, а слово "алгоритм" происходит от имени
средневекового арабского ученого Аль-Хорезми. Второе
"рождение" этой методологии пришлось на конец 40-х—начало 50-х годов
XX века и было обусловлено по крайней мере двумя
причинами. Первая из них — появление ЭВМ (компьютеров), хотя и скромных по
нынешним меркам, но тем не менее избавивших ученых от огромной по объему
рутинной вычислительной работы. Вторая - беспрецедентный социальный заказ —
выполнение национальных программ СССР и США по созданию ракетно-ядерного щита,
которые не могли быть реализованы традиционными методами. Математическое
моделирование справилось с этой задачей: ядерные взрывы и полеты ракет и
спутников были предварительно "осуществлены" в недрах ЭВМ с помощью
математических моделей и лишь затем претворены на практике. Этот успех во
многом определил дальнейшие достижения методологии, без применения которой в
развитых странах ни один крупномасштабный технологический, экологический или экономический проект теперь
всерьез не рассматривается (сказанное справедливо и по отношению к
некоторым социально-политическим проектам).
Сейчас
математическое моделирование вступает в третий принципиально важный этап своего
развития, "встраиваясь" в структуры так называемого информационного общества. Впечатляющий прогресс
средств переработки, передачи и хранения информации отвечает мировым тенденциям
к усложнению и взаимному проникновению различных сфер человеческой деятельности. Без владения информационными
"ресурсами" нельзя и думать о решении все более укрупняющихся
и все более разнообразных проблем, стоящих перед мировым сообществом. Однако
информация как таковая зачастую мало что дает для анализа и прогноза, для
принятия решений и контроля за их исполнением. Нужны надежные способы
переработки информационного "сырья в
готовый "продукт", т.е. в точное знание. История методологии математического моделирования
убеждает: она может и должна быть интеллектуальным ядром информационных
технологий, всего процесса информатизации общества. На первом этапе
выбирается (или строится) "эквивалент" объекта, отражающий в
математической форме важнейшие его свойства - законы, которым он подчиняется, связи, присущие составляющим его частям, и т.д.
Математическая модель (или ее фрагменты) исследуется теоретическими
методами, что позволяет получить важные предварительные знания об объекте. Второй этап — выбор (или разработка) алгоритма
для реализации модели на компьютере. Модель представляется в форме,
удобной для применения численных методов, определяется последовательность
вычислительных и логических операций, которые нужно произвести, чтобы найти
искомые величины с заданной точностью. Вычислительные алгоритмы должны не
искажать основные свойства модели и, следовательно, исходного объекта, быть экономичными и адаптирующимися к
особенностям решаемых задач и используемых компьютеров.На третьем этапе создаются программы,
"переводящие" модель и алгоритм на доступный компьютеру язык.
К ним также предъявляются требования экономичности и адаптивности. Их можно
назвать "электронным" эквивалентом
изучаемого объекта, уже пригодным для непосредственного испытания на
"экспериментальной установке" — компьютере. 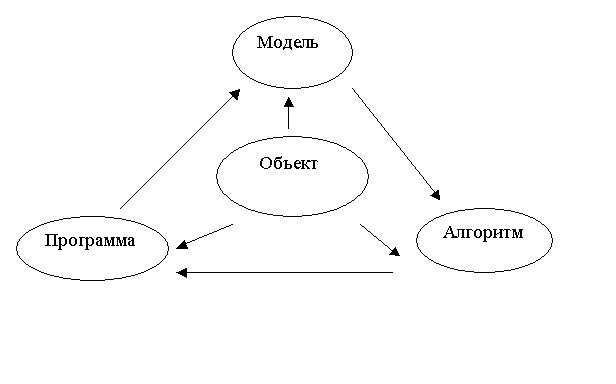
 Создав триаду "модель—алгоритм—программа",
исследователь получает в руки универсальный, гибкий и недорогой инструмент,
который вначале отлаживается, тестируется в "пробных" вычислительных
экспериментах. После того как адекватность (достаточное соответствие) триады
исходному объекту удостоверена, с моделью проводятся разнообразные и подробные "опыты", дающие все требуемые
качественные и количественные свойства и характеристики объекта. Процесс
моделирования сопровождается улучшением и уточнением, по мере необходимости,
всех звеньев триады. Рассматривая вопрос
шире, напомним, что моделирование присутствует почти во всех видах творческой
активности людей различных "специальностей" — исследователей и
предпринимателей, политиков и военачальников. Привнесение в эти сферы точного
знания помогает ограничить интуитивное умозрительное "моделирование",
расширяет поле приложений рациональных методов. Конечно же, математическое
моделирование плодотворно лишь при выполнении хорошо известных профессиональных
требований: четкая формулировка основных понятий и предположений, апостериорный анализ адекватности используемых моделей, гарантированная
точность вычислительных алгоритмов. Решая
проблемы информационного общества, было бы наивно уповать только на мощь компьютеров
и иных средств информатики. Постоянное совершенствование триады математического
моделирования и ее внедрение в современные информационно-моделирующие системы -
методологический императив. Лишь его выполнение дает возможность получать так нужную нам высокотехнологичную, конкурентоспособную
и разнообразную материальную и интеллектуальную продукцию.
Создав триаду "модель—алгоритм—программа",
исследователь получает в руки универсальный, гибкий и недорогой инструмент,
который вначале отлаживается, тестируется в "пробных" вычислительных
экспериментах. После того как адекватность (достаточное соответствие) триады
исходному объекту удостоверена, с моделью проводятся разнообразные и подробные "опыты", дающие все требуемые
качественные и количественные свойства и характеристики объекта. Процесс
моделирования сопровождается улучшением и уточнением, по мере необходимости,
всех звеньев триады. Рассматривая вопрос
шире, напомним, что моделирование присутствует почти во всех видах творческой
активности людей различных "специальностей" — исследователей и
предпринимателей, политиков и военачальников. Привнесение в эти сферы точного
знания помогает ограничить интуитивное умозрительное "моделирование",
расширяет поле приложений рациональных методов. Конечно же, математическое
моделирование плодотворно лишь при выполнении хорошо известных профессиональных
требований: четкая формулировка основных понятий и предположений, апостериорный анализ адекватности используемых моделей, гарантированная
точность вычислительных алгоритмов. Решая
проблемы информационного общества, было бы наивно уповать только на мощь компьютеров
и иных средств информатики. Постоянное совершенствование триады математического
моделирования и ее внедрение в современные информационно-моделирующие системы -
методологический императив. Лишь его выполнение дает возможность получать так нужную нам высокотехнологичную, конкурентоспособную
и разнообразную материальную и интеллектуальную продукцию.
Если же говорить о моделировании систем с участием "человеческого фактора", т.е. трудноформулируемого объекта, то к этим требованиям необходимо добавить аккуратное разграничение математических и житейские терминов, осторожное применение уже готового математического аппарата к изучению явлений и процессов, (предпочтителен путь "от задачи к методу", а не наоборот) и ряд других.