Технические науки/4.Транспорт

К.т.н. Петровский А.В., к.т.н. Петровский В.П.

Херсонский факультет Харьковского национального автодорожного университета, Херсонский национальный технический университет

ВИЗУАЛИЗАЦИИ ТРАНСПОРТНЫХ ПОТОКОВ СЕТЯМИ ПЕТРИ

Моделирование транспортных потоков является одним из приоритетных направлений изучения таких сложных организационных систем как транспортные системы. Необходимость оптимального распределения транспортных потоков в городах становится все актуальнее. Задачи оптимальной загрузки транспортных полос при наименьшем количестве конфликтных точек являются первостепенными задачами при планировании или анализе работы систем управления движением на перекрестках. В случаях исследования сложных перекрестков с большим количеством конфликтующих потоков (транспортных и пешеходных), возникает необходимость четкого визуального представления движения на перекрестке в целом для дальнейшего моделирования с помощью известных методов «движения вязкой жидкости» или «распространения ударной волны» в случае затора и т.д. Детальная схема перекрестка при этом не всегда помогает заметить конфликтные точки и имитировать ситуацию их возникновения или условия их устранения. Одним из вариантов инструмента построения имитационных моделей перемещения транспортных потоков на перекрестке является сеть Петри. Асинхронность работы сети поможет определить достижимость каждого потока при определенных условиях движения, заданных светофорной сигнализацией или дорожной разметкой и знаками.

Постановка задачи. Допустим, необходимо смоделировать работу перекрестка и, выявив возможные конфликтные точки, дать рекомендации по обеспечению безопасности их проезда. В качестве примера моделирования перекрестка с помощью сети Петри, рассмотрим сеть, спроектированную для площади Свободы города Херсона (рис.1).

Известно, что , где - конечная сеть (Р – множество условий-мест, Т – множество событий-переходов), при условии, что множество конечно, а и представляют собой функции кратности дуг и начальной разметки соответственно. Первая функция сопоставляет каждой дуге число , а вторая - сопоставляет каждому месту некоторое число . При разработке сети Петри сложность заключается в таком построении условий-мест и событий-переходов, чтобы избежать тупиковых ситуаций, т.е. когда при требуемой начальной разметке переход не срабатывает и условие-место не достижимо.

Общий порядок построения сети следующий:

1. Согласно детальной схемы перекрестка (количество полос в каждом доступном направлении, знаки приоритета, разрешенные направления движения) определить условия-места и события-переходы;

2. Построить функции входов и выходов, деревья достижимости по каждому из направлений движения.

3. Задать первоначальное распределение меток

С учетом правил проезда данного перекрестка (рис.1) были разработаны функции входов и выходов для , где и ;

при этом

k – направления движения на перекрестках, общим количеством v;.

l – состояния-переходы на k –ом направлении в количестве x;

b – условия регулировки движения (например светофорная сигнализация или знаки приоритета) общим количеством z;

r – условия-места количеством w на k –ом направлении движения.

Поскольку сеть Петри основана на асинхронном действии, построены деревья достижимости для каждого направления движения (1…16). Исследованы конфликтные точки системы управления движением на перекрестке: .

Первоначальная расстановка меток осуществляется в конфликтные точки воздействия и, затем, для исследования можно либо одновременно загружать метки в или по очереди. Для определения первоочередности проезда необходимо расставить приоритеты для событий-переходов:

- имеют максимальный приоритет;

-- средний приоритет;

- - минимальный приоритет.

Например, если есть возможность для выполнения состояний-переходов будет выполнен переход лишь как переход с наивысшим приоритетом; затем, в случае повторения ситуации и отсутствии метки в выполнятся переходы .

На основе разработанных функций входов и выходов, а также расстановки приоритетов для событий-переходов задача построения деревьев достижимости является достаточно простой и в данной работе не рассматривается.

Для уточнения способов воздействия необходимо иметь статистические данные интенсивности потоков в каждом направлении. Разработанная схема управления основана на использовании дорожной разметки и знаков приоритета.

Исходя из данных интенсивностей, можно было бы говорить о дальнейшей оптимизации движения с помощью светофорного регулирования.

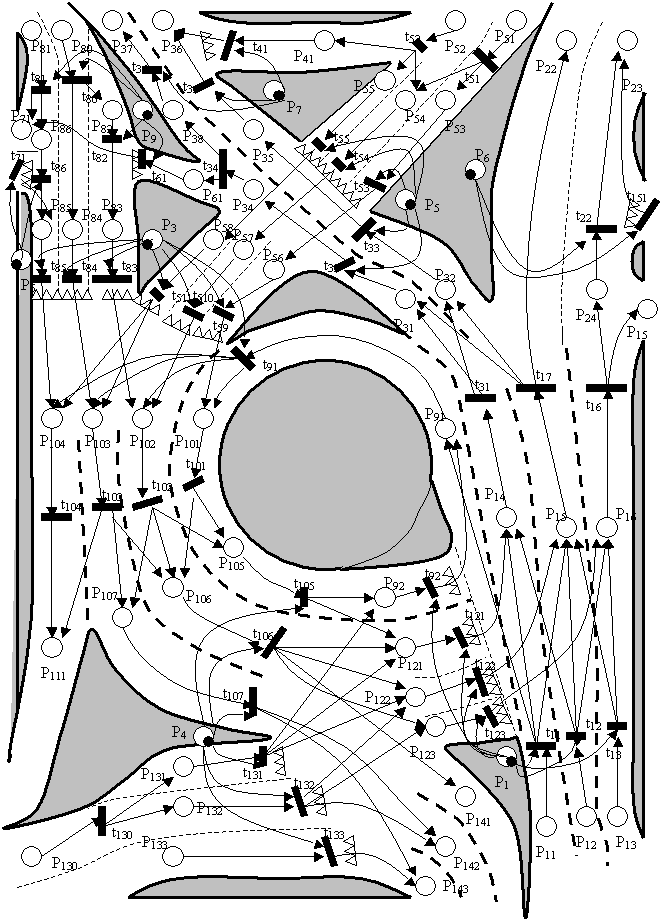
Рис.1 Транспортная развязка на площади Свободы г.Херсона

Выводы:

Преимущества использования сетей Петри при разработке имитационной модели распределения транспортных потоков на перекрестках:

- проигрывание конфликтных ситуаций для дальнейшего усовершенствования схемы управления перекрестком (применение/изменение дорожных знаков, ограничивающих направление движения, наличие приоритета, светофорной сигнализации в сложных местах);

- благодаря простоте графического отображения сети - быстрое проектирование визуального отображения распределения транспортных потоков при изменениях (добавления полосы для движения);

- возможность обрабатывать потоки параллельно;

- возможность разработки геоинформационной системы для данного перекрестка с последующим включением ее в геоинформационную сеть всего города.

Литература:

1. Котов В.Е., Сети Петри. – М.: Наука, 1984, - 160с.

2. Дж.Питерсон, Теория сетей Петри и моделирование систем. – М.: Мир, 1984, - 264с.

3. Кременец Ю.А., Технические средства организации дорожного движения: - Учебник для вузов. – М.: ИКЦ «Академкнига», 2005, - 279с.

4. Клинковштейн Г.И., Организация дорожного движения - М.: Транспорт, 2001, - 247с.

5. Правила дорожнього руху України. – К.: Вища школа, 2007, - 68с.

6. http://maps.join.ua/kherson/ - карта г.Херсона