УДК 519.6
Беляев Н. Н., Машихина
П. Б., Рябцева Н. П., Чорная А. Ю.
Днепропетровский
национальный университет
железнодорожного транспорта имени академика В. Лазаряна
численное исследование загрязнения атмосферы
и поверхностных вод
В работе рассматривается построение
математических моделей для прогноза уровня загрязнения воздушной среды и поверхностных вод при
разливе сжиженного аммиака.
Для моделирования
процесса загрязнения воздушной среды при испарении аммиака от свободной поверхности
зоны разлива (разлив в поддон) используется уравнение миграции примеси в
атмосфере:
 (1)
(1)
где С -
концентрация аммиака в атмосфере; u, v, w – компоненты вектора
скорости воздушной среды; μ = (μх,
μy, μz) – коэффициент турбулентной диффузии; Q – интенсивность испарения аммиака со
свободной поверхности; δ(r-ri) – дельта - функция Дирака; ri = (xi,, yi,, zi) – координаты источника испарения аммиака.
Для определения интенсивности
испарения аммиака со свободной поверхности используется эмпирическая зависимость
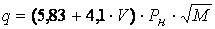
 ,
,
где V – скорость ветра; Рн
– давление насыщенных паров; М –
молекулярная масса.
При решении
задач о загрязнении атмосферы полагается, что профиль ветра описывается
зависимостью
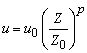 ,
,
где u0 – скорость ветра на высоте Z0=10 м от поверхности земли, u0; Z – текущее значение высоты; p=0,15 – параметр.
Для расчета загрязнения воды в реке
при попадании в нее аммиака делается предположение, что течение в русле потенциальное, тогда моделирующим уравнением будет уравнение вида
 ,
,
где  - потенциал,
- потенциал, 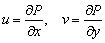 - компоненты вектора
скорости водной среды в реке.
- компоненты вектора
скорости водной среды в реке.
Для расчета процесса миграции аммиака по руслу реки используется модель градиентного типа
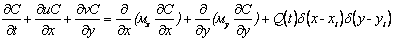 ,
,
где С – концентрация
загрязнителя в водной среде; u, v – компоненты вектора скорости водного
потока; 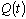 - интенсивность поступления аммиака в реку из аммиакопровода; t – время; xi, yi – координаты места утечки;
- интенсивность поступления аммиака в реку из аммиакопровода; t – время; xi, yi – координаты места утечки; 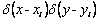 - дельта-функции Дирака; μ= (μх, μy) – коэффициент диффузии.
- дельта-функции Дирака; μ= (μх, μy) – коэффициент диффузии.
Метод решения. Для численного
интегрирования уравнений модели используется прямоугольная разностная сетка.
Уравнение миграции аммиака по руслу реки интегрируется с использованием
попеременно-треугольной неявной разностной схемы расщепления.
Выбор данной схемы обосновывается удобством ее применения
для расчета течений в областях различной геометрической формы.
Для численного
интегрирования уравнения для потенциала используется идея «установления решения по
времени», т. е. интегрируется уравнение вида
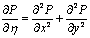 ,
,
где  - фиктивное время.
- фиктивное время.
Численное интегрирование
данного уравнения проводится с помощью неявного
попеременно-треугольного метода А. А. Самарского [4].
Испарение аммиака с водной поверхности реки приводит к загрязнению
атмосферы. Для моделирования этого процесса используется трехмерная модель градиентного
типа, аналогичная той, что применена для моделирования процесса переноса
примесив реке:
Таким образом, поступления аммиака с водной поверхности моделируется с помощью точеных источников и
дельта-функции. Интенсивность испарения
аммиака Q определяется
в процессе расчета с учетом процесса диффузии на границе «зеркало свободной
поверхности – атмосфера». Считается, что на свободной поверхности формируется слой, содержащий пары аммиака в условиях насыщения.
Данная модель используется также для моделирования процесса загрязнения атмосферы
при аварийных разливах сжиженного аммиака. Процесс расчета на базе модели
разбивается на два этапа:
ü на первом этапе на месте разлива
сжиженного аммиака задается первичное облако (размеры, форма, концентрация в
нем аммиака) и числено интегрируется приведенное выше трехмерное уравнение миграции примеси;
ü на втором этапе осуществляется расчет загрязнения
атмосферы за счет испарения аммиака от зоны разлива (задается форма зоны
разлива ее размеры и интенсивность испарения аммиака от зеркала свободной
поверхности).
Интенсивность испарения аммиака от зоны разлива рассчитывается путем применения эмпирической
зависимости.
На базе рассмотренной модели проведена серия вычислительных экспериментов
по моделированию загрязнения реки и атмосферы при различных аварийных сценариях.
 (1)
(1)![]()
![]() ,
,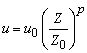 ,
,![]() ,
,![]() - потенциал,
- потенциал, ![]() - компоненты вектора
скорости водной среды в реке.
- компоненты вектора
скорости водной среды в реке.![]() ,
,![]() - интенсивность пост
- интенсивность пост![]() - дельта-ф
- дельта-ф![]() ,
,![]() - фиктивное время.
- фиктивное время.