СОВРЕМЕННЫЕ ИНФОРМАЦИОННЫЕ ТЕХНОЛОГИИ/4. Информационная безопасность

ЄЛІЗАРОВ А.Б., РЯБИЙ М.О., ШКАРУПА Д.В., ГОРІНШТЕЙН М.Л.

Національний авіаційний університет, Україна

ПІДВИЩЕННЯ КРИПТОСТІЙКОСТІ ДАНИХ НА БАЗІ МОДЕРНІЗОВАНОГО АЛГОРИТМУ DES

До недавнього часу американський стандарт шифрування DES вважався крипостійким. Багаторічний досвід експлуатації DES і його відкритість привели до того, що DES став одним з найпопулярніших алгоритмів з огляду перевірки тих або інших методів дешифрування й криптоаналізу. За увесь час існування алгоритму на нього було проведено чимало атак, при цьому були виявлені ряд недоліків. На сьогоднішній день було запропонована велика кількість пропозицій по удосконаленню DES [1].

Завдяки відкритості DES (вихідні тексти алгоритму і його програмні реалізації можна знайти у відкритих джерелах) активно використовують для захисту інформації, хоча це вже не є безпечним [5]. Вирішення цієї проблеми є досить актуальним. При її розв’язанні модернізований DES можна було б з упевненістю використовувати й надалі.

Метою статті є покращення криптостійкості алгоритму шифрування DES, його програмна реалізація і створення зручного інтерфейсу.

Для досягнення поставленої мети вирішуються такі основні задачі:

- дослідження недоліків DES і методів їх рішення;

- аналіз можливих атак і методів їх уникнення;

- на основі досліджених недоліків і можливих атак створення криптостійкої модернізації алгоритму;

- програмна реалізація модернізованого алгоритму і створення зручного інтерфейсу для роботи з ним.

Галузь застосування. Модифікований алгоритм шифрування DES може забезпечити захист інформації як в державних організаціях та і в приватній сфері [3].

Модернізація алгоритму шифрування DES

Проаналізувавши всі недоліки, існуючи на даний день модернізації алгоритму шифрування DES і сучасні методи криптоаналізу запропонуємо таку систему модернізації:

1. Збільшимо довжину ключа до 256 бітів. Атака методом повного перебору стане не практичною. Адже для цього потрібно буде перебрати 2²⁵⁶ можливих варіантів ключів. На сьогоднішній день, з урахуванням темпів розвитку комп’ютерної техніки, цього буде досить для того щоб вважати безпечним даний алгоритм ще протягом 10-ків років.

До того ж потрібно буде використовувати систему "розгортання" ключа, яка б задовольняла сучасним вимогам[2]:

1.1. Біти (символи) кожного ключового елемента повинні бути рівномовірні і статистично незалежний один від одного.

1.2. Біти (символи) кожного ключового елемента повинні бути статистично незалежними від бітів (символів) декількох сусідніх ключових елементів. Це умова повинне виконуватися в межах такої кількості кроків шифрування, на якому ще можна простежити статистичні залежності між бітами (символами) шифруємих блоків.

Для досягнення поставлених вимог будемо використовувати метод розширення ключа алгоритму шифрування SERPENT. При розширенні ключа способом запропонованим в алгоритмі SERPENT - всі біти ключа використаються для вироблення підключів раундів, до того ж знання одного ключового елемента не дозволяє відновити весь ключ шифрування [4,1]. Сам cпосіб розширення ключа буде наведений в наступному розділі.

2. Змінимо розмір S-блоків і зробимо їх залежними від ключа.

Слід зауважити, що саме S-блоки є єдиними нелінійними діями. І саме вони забезпечують захист проти диференційного і лінійного криптоаналізу. S-блок - це відображення m-бітових входів на n-бітових виходів. S-блок з m-бітовим входом і n-бітовим виходом називається m*n-бітовим S-блоком. У загальному випадку чим більше S-блоки, тим краще [3].

Чим більше S-блок, тим складніше виявити статистичні відхилення, потрібні для розкриття з використанням або диференціального, або лінійного криптоаналізу. Крім того, хоча випадкові S-блоки звичайно не оптимальні з погляду стійкості до диференціального і лінійному криптоаналізу, сильні S-блоки легше знайти серед S-блоків більшого розміру. Більшість випадкових S-блоків нелінійні, не вироджені і мають сильну стійкість до лінійного крипто аналізу [2].

Для забезпечення безпеки булеві функції, використовувані в S-блоках, повинні відповідати деяким умовам. Вони не повинні бути ні лінійними, ні афінними, ні навіть бути близькими до лінійного або афінного. Кількість нулів й одиниць повинно бути збалансованим, і не повинно бути ніяких кореляцій між різними комбінаціями бітів. При зміні на протилежний будь-якого вхідного біта вихідні біти повинні поводитися незалежно [3].

Змінимо розмір S-блоків з 6*4 на 4*4, і до того ж зробимо їх залежними від ключа. Оскільки криптоаналітик не буде знати точної структури S-блоків, це ускладнить застосування лінійного і диференціального криптоаіналізу.

3. Видалимо початкову і кінцеву перестановки.

Широко відомо що початкова і кінцева перестановки не покращують криптостійкість DES[3]. До того ж вони не ефективно реалізовуються програмно. Тому для збільшення швидкості шифрування їх просто видалим.

4. Ускладнимо структуру f-функції.

Чим складніша структура f-функції тим її складніше аналізувати.

5. Збільшимо кількість раундів шифрування

Цим самим ще підвищим криптостійкість у порівнянні з іншими методами шифрування. Так як лінійний і диференціальний криптоаналіз чутливі до кількості етапів – чим більша кількість етапів тим важче розкриття. При сучасному розвитку комп’ютерної техніки це збільшення буде не помітним.

6. Будемо використовувати метод “відбілення”.

Це таке перетворення, при якому виконується операція XOR над вхідним значенням блокового алгоритму й частиною ключа, і XOR над вихідним значенням блокового алгоритму й іншою частиною ключа. Зміст цих дій у тім, щоб перешкодити криптоаналітику відновити пари "відкритий текст/шифротекст" для досліджуваного блокового алгоритму. Метод змушує криптоаналітика вгадувати не тільки ключ алгоритму, але й одне із значень відбілювання. Оскільки операція XOR виконується до, і після виконання блокового алгоритму, цей метод вважається стійким до атаки "зустріч посередині". Проти диференціального й лінійного криптоаналізу такі міри забезпечують захист на рівні всього декількох бітів ключа. Але з обчислювальної точки зору це дуже дешевий спосіб підвищення надійності блокового алгоритму (рис.1).

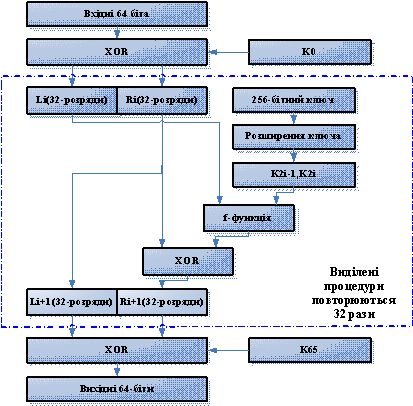
Рис. 1. Схема модернізації DES

Як і початковий DES цей алгоритм працює з 64-бітними блоками. Для шифрування і дешифрування використовується один і той самий алгоритм, різниця лиш у тому що підключі раундів подаються в протилежному порядку. Слід зауважити що довжина ключа тепер становить 256 біт. Цим стає неможливий на сучасному етапі розвитку обчислювальної техніки перебір ключа.

Основні етапи алгоритму:

1. Перетворення починається з додаванням по модулю 2 вхідного 64-бітного блоку з підключем K₀. Слід зауважити, що ми відмовилися від початкової так і від кінцевої перестановки. Це було зроблено для збільшення швидкості шифрування для програмних реалізацій даного алгоритму. Оскільки в даній роботі цей алгоритм буде реалізований програмно цим можна виграти в швидкості шифрування. До того ж широко відомо що ці перестановки не впливають на криптостійкість алгоритму [5]. Тому при їх усуненні криптостійкість не знижується.

2. 64-бітний блок ділиться на дві 32-бітні частини L₀ і R₀. Далі як і в початковому DES виконуються n-раз однотипні процедури. В алгоритмі DES їх було 16, в даній модернізації їх 32. З сучасним розвитком обчислювальної техніки цю різницю користувач практично не замітить. Різниця буде долі секунди. До того ж відомо що багато методів криптоаналізу(а саме лінійний і диференціальний криптоаналіз) чутливі до кількості етапів[5]. Цим можна підвищити криптостійкість модернізованого алгоритму.

Отже опишемо ці процедури:

2.1. враховуючи номер ітерації генеруються підключи раундів, для кожного раунду використовуються двоє 64-бітних підключів, а в початковому DES один 48-бітний;

2.2. за допомогою функції f(L_i,K_2i-1,K_2i) генерується 32-розрядний вихідний код;

2.3. виконується операція XOR для R_і і f(L_i,K_i), результат позначається R_і+1;

2.4. виконується операція присвоєння L_і+1=Rі.

3. Кінцева операція це додавання по модулю 2 вхідного 64-бітного блоку з підключем K₃₃. Після чого отримаємо кінцеві вихідні біти. Спосіб додавання по модулю 2 на початку і на прикінці до вхідного і відповідно вихідного блоку деяких підключів називається відбілюванням. Цей метод вважається стійким до атаки "зустріч посередині". Проти диференціального й лінійного криптоаналізу такі міри забезпечують захист на рівні всього декількох бітів ключа. Але все одно використання цього методу покращує криптостійкість модернізованого DES.

Процедура розширення ключа.

В статті запропонований спосіб розширення ключа, який використовується в алгоритмі шифрування Serpent, але трошки в модифікованому вигляді. Даний метод розширення ключа актуальний тим що він задовольняла сучасним вимогам [4].

Фактично, ключ може мати довільний розмір, менший 256. Такий "неповний" ключ перед виконанням його розширення доповнюється за наступним правилом:

1. Ключ доповнюється одним одиничним бітом праворуч.

2. Потім ключ доповнюється праворуч нульовими бітами до досягнення 256-бітного розміру.

Тільки після цього виконується процедура розширення ключа, що складається з наступних кроків[1]:

1. 256-бітний доповнений (при необхідності) ключ шифрування представляється у вигляді 8 32-бітних слів, позначуваних w_-8...w_-1.

2. Дані слова використаються як вихідні значення для обчислення проміжного ключа - послідовності w₀...w₁₃₅:

w_i = (w_i-8 w_i-5 w_i-3 w_i-1 i) <<< 11.

де = 9E3779B9 у шістнадцятирічному записі.

Таким чином формується велика кількість 32-бітних слів.

3. Обчислюються підключі з використанням таблиць замін S₀...S₇:

K₀ = S₃({w₀, w₁}),
K₁ = S₂({w₂, w₃}),
K₂ = S₁({w₄, w₅}),
K₃ = S₀({w₆, w₇}),
K₄ = S₇({w₈, w₉}),
K₅ = S₆({w₁₀, w₁₁, }),
...
K₆₄ = S₄({w₁₂₈, w₁₂₉}),
K₆₅ = S₃({w₁₃₀, w₁₃₁}).

В самому алгоритму шифрування Serpent шукають 128 бітні підключі. В даному методі модернізації DES отримуємо 64 бітні підключі.

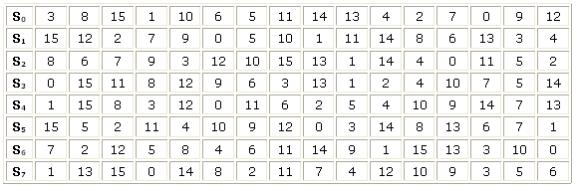
S-блоки представлять собою блоки замін 4*4. Ці S-блоки взяті з того ж алгоритму шифрування Serpent.

На рис. 2. показано як саме використовуються задані S-блоки.

Блок даних розбивається на маленькі 4 бітні підблоки. Після чого виконується таблична заміна 4*4 біт. Отриманий результат приєднується назад у блок.

Рис. 1.2. Використання S-блоків

В табл. 1 наведені всі S-блоки.

Таблиця 1

Таблиця S-блоків [1]

При використанні такого розширення всі біти ключа використовуються для генерації підключів раундів, до того ж знання одного ключового елемента не дозволяє відновити весь ключ шифрування [2].

Опишемо функцію f (рис. 1.3.). Вона найбільше змінилась якщо порівнювати з справжнім DES. Але слід пам’ятати що саме в ній використовуються нелінійні перетворення, що і забезпечують криптостійкість DES.

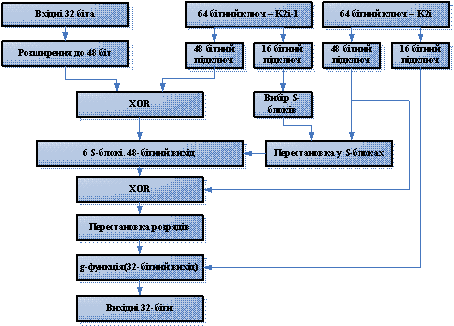
Рис. 3. Схема модернізованої f-функції

Опишемо її поетапно:

1. Спочатку 32 вхідні розряди розширюються до 48 біт, при цьому деякі розряди повторюються. Схема цього розширення показана в табл. 2 (номера відповідають номерам біт вихідного 32-розрядного коду).

Таблиця 2

Розширення вхідного блоку до 48 біт

32	1	2	3	4	5
4	5	6	7	8	9
8	9	10	11	12	13
12	13	14	15	16	17
16	17	18	19	20	21
20	21	22	23	24	25
24	25	26	27	28	29
28	29	30	31	32	1

Використовується така сама схема як і в оригінальному DES.

2. 64-бітний підключ K_2i-1 ділиться на дві частини. В одній буде 48 біт, в іншій 16. До першої частини увійдуть старших 48 біт, до другої 16 молодших біт підключа K_2i-1.

3. 48-бітний підключ утворений в пункті 2, складається по модулю 2 з утвореною в першому пункті 48-бітним блоком.

4. Іде вибір пари S-блоків, які будуть використовуватись пізніше.

Для цього 16-бітний підключ сформований в пункті 2, ділиться на дві частини по 8 біт. Кожна з цих частин використовується для вибору номеру S-блоку, який буде використовуватись.

Опишемо алгоритм вибору S-блоку. Нам дано вісім біт для знаходження S-блоку: a₁a₂a₃a₄a₅a₆a₇a₈. Після чого розділимо їх на дві частини

a₁a₂a₃a₄ і a₅a₆a₇a_8. Додамо їх по модулю 8. В результаті отримаємо число від 0 до 7, яке і буде номером S-блоку. Отже ми знайдемо пару S-блоків, які будуть використовуватися далі.

Слід зауважити це ті самі S-блоки, які використовувалися в при генеруванні підключів (див. табл. 1).

5. Розкладаємо інший 64-бітний ключ теж на дві частини. В одній буде 48 біт, в іншій 16.

6. За допомогою отриманого 48-бітного підключа міняємо порядок колонок в S-блоках.

Ось як це виконується. Якщо перший біт 48-бітного ключа дорівнює 1 тоді міняться місцями 1,2 елементи S-матриць Якщо другий біт дорівнює 1 тоді міняються 2, 3 елементи S-матриць. Якщо 3 біт дорівнює 1 міняються 4 і 5 елементи масиву. І так продовжується 48 раз поки не будуть враховані всі біти 48-бітного підключа. Так сформуються S-блоки залежні від ключа.

Пунктами 4-6 формуються S-блоки в залежності від підключів раундів.

7. Далі результат отриманий в пункті 3 пропускається через S-матриці.

Для цього блок розбиваються по 8 біт, після чого перші 4 з послідовності проходять через першу таблицю замін, інші 4 через другу таблицю замін. Після цієї операції отримаємо вихідні 48 біт.

8. Підключ який використовувався в пункті 6 додамо по модулю 2 з результатом підпункту 7. На виході знову отримали 48 біт.

9. Над результатом пункту 8 здійснюється перестановка відповідно до схеми див. табл. 3 (числа являють собою порядкові номери біт).

Таблиця 3

Перестановка розрядів функції f

16	7	20	21	29	12
28	17	1	15	23	26
5	18	31	10	2	8
24	14	32	27	3	9
19	13	30	6	22	11
4	25	48	46	44	42
40	38	36	34	47	45
43	41	39	37	35	33

10. Результат пункту 9 і 16-бітний підключ пункту 5 подаються в функцію g. На виході якої з 48 вхідних біт залишиться кінцеві 32 вихідних біти.

Опишемо функцію g (рис. 4.):

1. Вхідні 48 біт розбиваються на чотири 12-бітних підблоки.

2. Підраховується кількість 1-ць в 16-бітному підключі

3. Потім циклічно зрушуємо отримані в пункті 1 12-бітні блоки на число підраховане в пункті 2.

Операція циклічного зсуву вперше була застосована в алгоритмі RC5. Вважається, що саме революційна ідея зрушення на змінне число біт привернула увагу криптоаналітиків до алгоритму RC5 - він став одним з алгоритмів, найбільш вивчених на предмет можливих атак [3]. RC5 майже неможливо розкрити методом лінійного криптоаналізу. Багато в чому цю властивість алгоритму визначено наявністю операції циклічного зрушення на змінне число біт. Тому використовуємо цей метод для покращення криптостійкості модернізованого DES.

4. Обрізаємо перші чотири біти з отриманих 12-бітних підблоків.

5. Це все об’єднаємо в 32-бітний вихід

Рис. 4. Структура g-функції

Результатом виконаної роботи є підвищена криптостійкість данного алгоритму:

1. Довжина ключа рівна 256 біт. Атака методом повного перебору не можлива при сучасному розвиткові обчислювальної техніки, з запасом ще у десятки років.

2. При шифруванні використовуємо S-блоки залежні від ключа. Тому при аналізі криптоаналітикові прийдеться враховувати можливі варіанти S-блоків.

3. Використовується не 16, а 32 раунди шифрування. Цим самим покращується криптостійкість проти диференціального і лінійного криптоаналізу.

4. Використовується метод “відбілювання”. Який теж покращує криптостійкість данного методу.

Література:

1. Методы криптоанализа. – <http://www.i2r.ru>.

2. Алгоритмы DES и Тройной DES. –<http://www.skgtu.ru>.

3. Коробейников А.Г., Гатчин Ю.А. Математические основы криптологии: Учебное пособие. – СПб ГУ ИТМО, 2004. – 106 с.

4. Алгоритмы блочного шифрования. – < http://www.az.ru/defence>.

5. Алгоритм DES. – <http://book.itep.ru>.