Д.п.н., профессор О.С.Сатыбалдиев
Казахский национальный технический университет им. К.И.Сатпаева, Республика
Казахстан
Критерий конечности типа резольвенты несамосопряженного оператора
Штурма-Лиувилля
Пусть ![]() -действительная, бесконечно гладкая положительная, а
-действительная, бесконечно гладкая положительная, а ![]() -комплексная локальная суммируемая в
-комплексная локальная суммируемая в ![]() функции, причем
функции, причем
![]() (1)
(1)
Обозначим через ![]() замыкание в
замыкание в ![]() оператора
оператора ![]() определенного на
множестве
определенного на
множестве ![]() равенством
равенством
![]()
Всюду в этой работе мы предполагаем
выполненным следующие условия:
1) для каждого достаточно большого ![]() существует постоянное
число
существует постоянное
число ![]() такое, что
такое, что
![]() при
при 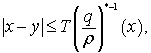 (2)
(2)
где
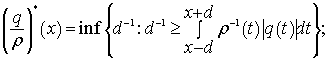 (3)
(3)
2) существует вполне непрерывный оператор ![]() обратный к
обратный к ![]() и определенный на
всем
и определенный на
всем ![]()
Пусть ![]() оператор сопряженный
к
оператор сопряженный
к ![]() Тогда
Тогда ![]() является замыканием в
является замыканием в
![]() оператора
оператора ![]() определенного на
определенного на ![]() равенством
равенством
![]()
Заметим, что при выполнении условия 2) оператор ![]() сопряженный к
сопряженный к ![]() также вполне
непрерывен и обратим, причем
также вполне
непрерывен и обратим, причем ![]() Но тогда вполне
непрерывен и обратим неотрицательный самосопряженный оператор
Но тогда вполне
непрерывен и обратим неотрицательный самосопряженный оператор ![]() и обратным неотрицательный
квадратный корень из него, т.е. оператор
и обратным неотрицательный
квадратный корень из него, т.е. оператор ![]()
Известно также, что ![]() для всех
для всех ![]()
Обозначим ![]() Тогда
Тогда ![]() и
и ![]() для всех
для всех ![]() Нетрудно заметить,
что справедливы соотношения
Нетрудно заметить,
что справедливы соотношения
![]()
![]()
![]()
![]() и
и ![]() (4)
(4)
для всех ![]()
В самом деле, для всякой функции ![]()
![]() Из этого соотношения
и из определения
Из этого соотношения
и из определения ![]() а также замкнутости
оператора
а также замкнутости
оператора ![]() вытекают равенства
(4). Следуя [1], собственные числа оператора
вытекают равенства
(4). Следуя [1], собственные числа оператора ![]() называем
называем ![]() -числами оператора
-числами оператора ![]() и обозначим их
и обозначим их ![]() так что
так что ![]() Числа
Числа ![]() будем называть
будем называть ![]() числами оператора
числами оператора ![]() т.е.
т.е. ![]()
Пуст для каждого ![]() обозначает количество
обозначает количество
![]() чисел оператора
чисел оператора ![]() не превосходящих
не превосходящих ![]()
![]()
![]()
Справедлива следующая
Теорема1. [2,с.23]. Пусть выполнены условия 1)-2) и ![]() Тогда справедливы
оценки
Тогда справедливы
оценки
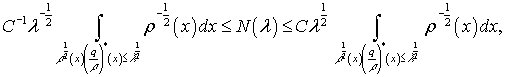 (5)
(5)
где ![]() -постоянная, зависящая только от постоянной
-постоянная, зависящая только от постоянной ![]() из условия 1).
из условия 1).
Теорема2. Пусть выполнены условия 1)-2) и ![]()
Тогда
а) оператор ![]() принадлежит классу
принадлежит классу ![]() в том и только в том
случае, если
в том и только в том
случае, если

б) справедливы оценки

где ![]() -постоянная, зависящая от
-постоянная, зависящая от ![]() и от постоянной
и от постоянной ![]() из условия (1).
из условия (1).
Доказательство. Заметим, что

Отсюда используя неравенство (3),
справедливы при ![]() и выполнены условий 1)-2)
(см. теоремы1), нетрудно получить оценки
и выполнены условий 1)-2)
(см. теоремы1), нетрудно получить оценки

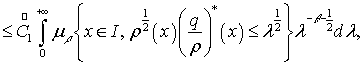
где
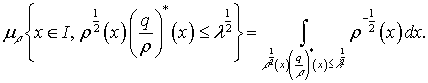
С другой стороны при достаточно большем ![]()
![]() и
и ![]() справедливы следующие
равенства
справедливы следующие
равенства



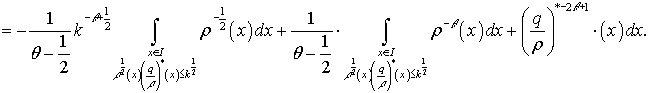
Далее, рассуждая также, как и в
работах ([3], [4]), получаем оценки

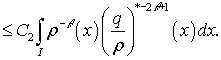
Из последних оценок и оценок (5) вытекает
утверждение б) теоремы. Утверждение а) теоремы является следствием утверждения
б).
Теорема2 доказана.
Литература:
1. Гохбер И.Ц., Крейн М.Г., введение в теорию линейных несамосопряженных операторов, М,
Наука, 1965.
2. Сатыбалдиев О.С. Об оценках ![]() -чисел и полноте системы корневых векторов некоторых
дифференциальных операторов, конд....дис., Алма-Ата, 1988.
-чисел и полноте системы корневых векторов некоторых
дифференциальных операторов, конд....дис., Алма-Ата, 1988.
3.Отелбаев М., Оценки собственных чисел сингулярных
дифференциальных операторов. Матем. Заметки, т.20, №6, 1976, с. 859-867.
4. Розенблюм Г.В., Об оценках спектора оператора Шредингера.
Вкн.: Проблемы математического анализа, ЛГУ, вып.5, 1975. с. 152-165.